Biết \(G\) là trọng tâm tam giác \(ABC\). Mệnh đề nào sau đây đúng?
| \(\overrightarrow{AG}+\overrightarrow{BG}=\overrightarrow{CG}\) | |
| \(\overrightarrow{GA}+\overrightarrow{GB}=\overrightarrow{CG}\) | |
| \(\overrightarrow{GA}-\overrightarrow{GB}=\overrightarrow{CG}\) | |
| \(\overrightarrow{GA}-\overrightarrow{GB}=\overrightarrow{GC}\) |
Cho tam giác \(ABC\) có trọng tâm \(G\), \(M\) là trung điểm cạnh \(BC\). Mệnh đề nào sau đây sai?
| \(\overrightarrow{MB}+\overrightarrow{MC}=\vec{0}\) | |
| \(\overrightarrow{AB}+\overrightarrow{AC}=2\overrightarrow{AM}\) | |
| \(\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\vec{0}\) | |
| \(\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}=-3\overrightarrow{MG}\) |
Cho tam giác \(ABC\) có \(G\) là trọng tâm. Mệnh đề nào sau đây sai?
| \(\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}=3\overrightarrow{MG}\) | |
| \(\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\vec{0}\) | |
| \(\overrightarrow{GB}+\overrightarrow{GC}=2\overrightarrow{GA}\) | |
| \(3\overrightarrow{AG}=\overrightarrow{AB}+\overrightarrow{AC}\) |
Cho tam giác \(ABC\) có \(G\) là trọng tâm và \(I\) là trung điểm cạnh \(BC\). Đẳng thức nào sau đây đúng?
| \(\overrightarrow{GA}=2\overrightarrow{GI}\) | |
| \(\overrightarrow{IG}=-\dfrac{1}{3}\overrightarrow{IA}\) | |
| \(\overrightarrow{GB}+\overrightarrow{GC}=2\overrightarrow{GI}\) | |
| \(\overrightarrow{GB}+\overrightarrow{GC}=2\overrightarrow{GA}\) |
Cho tam giác \(ABC\) có \(M\) là điểm thỏa mãn \(\overrightarrow{MA}-\overrightarrow{MB}+\overrightarrow{MC}=\vec{0}\). Mệnh đề nào sau đây sai?
| \(MABC\) là hình bình hành | |
| \(\overrightarrow{AM}+\overrightarrow{AB}=\overrightarrow{AC}\) | |
| \(\overrightarrow{BA}+\overrightarrow{BC}=\overrightarrow{BM}\) | |
| \(\overrightarrow{MA}=\overrightarrow{BC}\) |
Cho tam giác \(ABC\) có $M$ là điểm thỏa mãn \(\overrightarrow{MB}+\overrightarrow{MC}=\overrightarrow{AB}\). Xác định vị trí điểm \(M\).
| \(M\) là trung điểm cạnh \(AC\) | |
| \(M\) là trung điểm cạnh \(AB\) | |
| \(M\) là trung điểm cạnh \(BC\) | |
| \(M\) là điểm thứ tư của hình bình hành \(ABCM\) |
Cho tam giác \(ABC\), trung tuyến \(AM\). Đẳng thức nào sau đây không đúng?
| \(\overrightarrow{MA}+\overrightarrow{MB}=\overrightarrow{0}\) | |
| \(\overrightarrow{MB}+\overrightarrow{MC}=\overrightarrow{0}\) | |
| \(\overrightarrow{AB}+\overrightarrow{AC}=2\overrightarrow{AM}\) | |
| \(\overrightarrow{MB}-\overrightarrow{MC}=\overrightarrow{CB}\) |
Cho tam giác \(ABC\) có \(M\) là trung điểm của \(BC\), \(I\) là trung điểm của \(AM\). Khẳng định nào sau đây đúng?
| \(\overrightarrow{IB}+2\overrightarrow{IC}+\overrightarrow{IA}=\vec{0}\) | |
| \(\overrightarrow{IB}+\overrightarrow{IC}+2\overrightarrow{IA}=\vec{0}\) | |
| \(2\overrightarrow{IB}+\overrightarrow{IC}+\overrightarrow{IA}=\vec{0}\) | |
| \(\overrightarrow{IB}+\overrightarrow{IC}+\overrightarrow{IA}=\vec{0}\) |
Cho tam giác \(ABC\) có \(D,\,E,\,F\) lần lượt là trung điểm các cạnh \(BC,\,CA,\,AB\). Hệ thức nào sau đây đúng?
| \(\overrightarrow{AD}+\overrightarrow{BE}+\overrightarrow{CF}=\overrightarrow{AB}+\overrightarrow{AC}+\overrightarrow{BC}\) | |
| \(\overrightarrow{AD}+\overrightarrow{BE}+\overrightarrow{CF}=\overrightarrow{CA}+\overrightarrow{BC}+\overrightarrow{AC}\) | |
| \(\overrightarrow{AD}+\overrightarrow{BE}+\overrightarrow{CF}=\overrightarrow{AE}+\overrightarrow{BF}+\overrightarrow{CD}\) | |
| \(\overrightarrow{AD}+\overrightarrow{BE}+\overrightarrow{CF}=\overrightarrow{BA}+\overrightarrow{BC}+\overrightarrow{AC}\) |
Cho tam giác \(ABC\) có \(AB=AC\) và đường cao \(AH\). Đẳng thức nào sau đây đúng?
| \(\overrightarrow{AB}+\overrightarrow{AC}=\overrightarrow{AH}\) | |
| \(\overrightarrow{HA}+\overrightarrow{HB}+\overrightarrow{HC}=\vec{0}\) | |
| \(\overrightarrow{HB}+\overrightarrow{HC}=\vec{0}\) | |
| \(\overrightarrow{AB}=\overrightarrow{AC}\) |
Cho tam giác \(ABC\) với \(M\) là trung điểm cạnh \(BC\). Mệnh đề nào sau đây đúng?
| \(\overrightarrow{AM}+\overrightarrow{MB}+\overrightarrow{BA}=\vec{0}\) | |
| \(\overrightarrow{MA}+\overrightarrow{MB}=\overrightarrow{AB}\) | |
| \(\overrightarrow{MA}+\overrightarrow{MB}=\overrightarrow{MC}\) | |
| \(\overrightarrow{AB}+\overrightarrow{AC}=\overrightarrow{AM}\) |
Cho tam giác \(ABC\). Khẳng định nào sau đây đúng?
| \(\overrightarrow{AB}+\overrightarrow{AC}=\overrightarrow{BC}\) | |
| \(\overrightarrow{AB}+\overrightarrow{CA}=\overrightarrow{CB}\) | |
| \(\overrightarrow{CA}+\overrightarrow{BA}=\overrightarrow{CB}\) | |
| \(\overrightarrow{AA}+\overrightarrow{BB}=\overrightarrow{AB}\) |
Trong không gian, cho tứ diện $ABCD$ có trọng tâm $S$. Gọi $G$ là trọng tâm tam giác $BCD$, $M$ và $N$ lần lượt là trung điểm của $AB$, $CD$. Mệnh đề nào sau đây là sai?
| $S$ là trung điểm đoạn $MN$ | |
| $\overrightarrow{SA}+\overrightarrow{SB}+\overrightarrow{SC}+\overrightarrow{SD}=\overrightarrow{0}$ | |
| $S$ nằm trên đoạn $AG$ sao cho $SA=3SG$ | |
| $\overrightarrow{SA}+\overrightarrow{SB}+\overrightarrow{SC}+\overrightarrow{SD}=\overrightarrow{0}$ |
Trong không gian, điểm $S$ là trọng tâm của tam giác $ABC$ nếu
| $\overrightarrow{SA}+\overrightarrow{SB}+\overrightarrow{SC}=\overrightarrow{0}$ | |
| $\overrightarrow{SA}+\overrightarrow{SB}=\overrightarrow{SC}$ | |
| $\overrightarrow{SA}+\overrightarrow{SB}=\overrightarrow{0}$ | |
| $\overrightarrow{AB}+\overrightarrow{AC}=\overrightarrow{AS}$ |
Cho tứ diện $ABCD$ có $G$ là trọng tâm tam giác $BCD$. Mệnh đề nào sau đây không đúng?
| $\overrightarrow{AB}+\overrightarrow{AC}+\overrightarrow{AD}=3\overrightarrow{AG}$ | |
| $\overrightarrow{GB}+\overrightarrow{GC}+\overrightarrow{GD}=\overrightarrow{0}$ | |
| $\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}$ | |
| $\overrightarrow{AB}+\overrightarrow{AC}+\overrightarrow{AD}-3\overrightarrow{AG}=\overrightarrow{0}$ |
Cho tam giác \(ABC\). Có bao nhiêu điểm \(M\) thỏa mãn \(\left|\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}\right|=1\)?
| \(1\) | |
| \(2\) | |
| \(0\) | |
| Vô số |
Cho hình bình hành \(ABCD\), tâm \(M\). Mệnh đề nào sau đây sai?
| \(\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}\) | |
| \(\overrightarrow{AB}+\overrightarrow{AD}=\overrightarrow{AC}\) | |
| \(\overrightarrow{BA}+\overrightarrow{BC}=2\overrightarrow{BM}\) | |
| \(\overrightarrow{MA}+\overrightarrow{MB}=\overrightarrow{MC}+\overrightarrow{MD}\) |
Cho hình bình hành \(ABCD\). Đẳng thức nào sau đây đúng?
| \(\overrightarrow{AC}+\overrightarrow{BD}=2\overrightarrow{BC}\) | |
| \(\overrightarrow{AC}+\overrightarrow{BD}=\overrightarrow{AB}\) | |
| \(\overrightarrow{AC}-\overrightarrow{BD}=2\overrightarrow{CD}\) | |
| \(\overrightarrow{AC}-\overrightarrow{AD}=\overrightarrow{CD}\) |
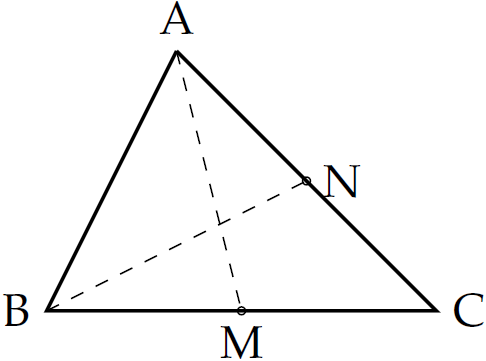
Bạn Thùy đặt một tấm bìa cứng hình tam giác (như hình vẽ) lên đầu một ngòi bút nhưng tấm bìa không bị rơi. Hỏi bạn Thùy đã đặt ngòi bút tại điểm nào của tấm bìa?
| Điểm \(A\) | |
| Trung điểm \(M\) | |
| Trung điểm \(N\) | |
| Giao điểm \(AM\) và \(BN\) |
Cho hình bình hành \(ABCD\) tâm \(O\). Hãy tìm đẳng thức đúng.
| \(\overrightarrow{OA}+\overrightarrow{OB}=\overrightarrow{AB}\) | |
| \(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}-\overrightarrow{OD}=\vec{0}\) | |
| \(\overrightarrow{OA}+\overrightarrow{OB}=\overrightarrow{OC}-\overrightarrow{OD}\) | |
| \(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{OD}=\vec{0}\) |
