Cho tam giác $ABC$ có độ dài ba cạnh lần lượt là $3$, $5$, $6$. Tính bán kính đường tròn nội tiếp của $ABC$.

	$r=\dfrac{\sqrt{14}}{7}$
	$r=\dfrac{2\sqrt{14}}{7}$
	$r=2\sqrt{14}$
	$r=\dfrac{6\sqrt{77}}{7}$

Một tam giác có ba cạnh là \(26\), \(28\), \(30\). Bán kính vòng tròn nội tiếp là

	\(16\)
	\(8\)
	\(4\)
	\(4\sqrt{2}\)

Tam giác \(ABC\) vuông tại \(A\) có \(AC=6\)cm, \(BC=10\)cm. Đường tròn nội tiếp tam giác có bán kính \(r\) bằng

	\(1\)cm
	\(\sqrt{2}\)cm
	\(2\)cm
	\(3\)cm

Tam giác $ABC$ có độ dài ba cạnh lần lượt là $21$cm, $17$cm và $10$cm. Tính bán kính đường tròn ngoại tiếp.

	$R=\dfrac{85}{8}$cm
	$R=\dfrac{85}{2}$cm
	$R=\dfrac{7}{4}$cm
	$R=\dfrac{7}{2}$cm

Gọi \(R\) là bán kính đường tròn ngoại tiếp tam giác \(ABC\). Khẳng định nào sau đây sai?

	\(\dfrac{a}{\sin A}=\dfrac{b}{\sin B}=\dfrac{c}{\sin C}=2R\)
	\(a=2R\sin A\)
	\(a=c\dfrac{\sin A}{\sin C}\)
	\(\dfrac{a}{b}=\dfrac{\sin B}{\sin A}\)

Tam giác đều nội tiếp đường tròn bán kính \(R=4\)cm có diện tích là

	\(12\sqrt{3}\)cm\(^2\)
	\(13\sqrt{2}\)cm\(^2\)
	\(13\)cm\(^2\)
	\(15\)cm\(^2\)

Tam giác \(ABC\) với \(a=2\), \(b=\sqrt{6}\), \(c=1+\sqrt{3}\) có bán kính đường tròn ngoại tiếp bằng

	\(R=\dfrac{\sqrt{2}}{3}\)
	\(R=\dfrac{\sqrt{2}}{2}\)
	\(R=\sqrt{2}\)
	\(R=\sqrt{3}\)

Một tam giác có ba cạnh là \(52,\,56,\,60\). Bán kính đường tròn ngoại tiếp tam giác đó là

	\(\dfrac{65}{4}\)
	\(40\)
	\(32,5\)
	\(65,8\)

Tam giác \(ABC\) vuông cân tại \(A\) có \(AB=AC=a\). Đường trung tuyến \(BM\) có độ dài là

	\(\dfrac{3a}{2}\)
	\(a\sqrt{2}\)
	\(a\sqrt{3}\)
	\(\dfrac{a\sqrt{5}}{2}\)

Cho tam giác \(ABC\) có \(BC=10\), \(\widehat{A}=30^\circ\).Tính bán kính đường tròn ngoại tiếp tam giác \(ABC\).

	\(10\)
	\(\dfrac{10}{\sqrt{3}}\)
	\(10\sqrt{3}\)
	\(5\)

Cho tam giác \(ABC\) có \(BC=a\), \(\widehat{BAC}=120^\circ\). Bán kính đường tròn ngoại tiếp \(\Delta ABC\) là

	\(R=\dfrac{a\sqrt{3}}{2}\)
	\(R=\dfrac{a}{2}\)
	\(R=\dfrac{a\sqrt{3}}{3}\)
	\(R=a\)

Cho tam giác \(ABC\) có \(\widehat{B}=120^\circ\), cạnh \(AC=2\sqrt{3}\)cm. Bán kính \(R\) của đường tròn ngoại tiếp tam giác \(ABC\) bằng

	\(R=2\)cm
	\(R=4\)cm
	\(R=1\)cm
	\(R=3\)cm

Trong tam giác \(ABC\) có

	\(a=2R\cos A\)
	\(a=2R\sin A\)
	\(a=2R\tan A\)
	\(a=R\sin A\)

Cho khối lăng trụ đứng $ABC.A'B'C'$ có đáy $ABC$ là tam giác vuông cân tại $A$, $AB=2a$. Góc giữa đường thẳng $BC'$ và mặt phẳng $(ACC'A')$ bằng $30^\circ$. Thể tích của khối lăng trụ đã cho bằng

	$3a^3$
	$a^3$
	$12\sqrt{2}a^3$
	$4\sqrt{2}a^3$

Tính thể tích $V$ của vật thể giới hạn bởi hai mặt phẳng $x=0,\,x=\pi$. Biết rằng thiết diện của vật thể cắt bởi mặt phẳng vuông góc với $Ox$ tại điểm có hoành độ $x\,(0\leq x\leq\pi)$ là một tam giác vuông cân có cạnh huyền bằng $\sin x+2$.

	$\dfrac{7\pi}{6}+1$
	$\dfrac{9\pi}{8}+1$
	$\dfrac{7\pi}{6}+2$
	$\dfrac{9\pi}{8}+2$

Cho hình lăng trụ đứng $ABC.A'B'C'$ có đáy $ABC$ là tam giác vuông cân tại $B$ và $AB=4$ (tham khảo hình bên).

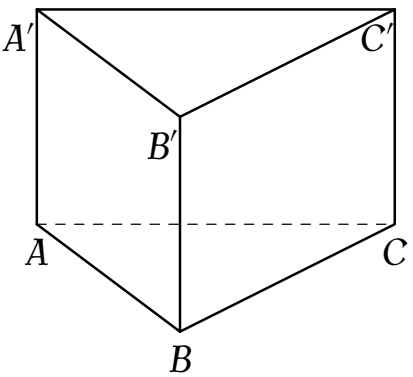
Khoảng cách từ $C$ đến mặt phẳng $\left(ABB'A'\right)$ bằng

	$2\sqrt{2}$
	$2$
	$\sqrt{2}$
	$4$

1. Giả sử hai hàm số $y=f\left(x\right)$ và $y=f\left(x+1\right)$ đều liên tục trên đoạn $\left[0;2\right]$ và $f\left(0\right)=f\left(2\right)$. Chứng minh phương trình $f\left(x\right)-f\left(x+1\right)=0$ luôn có nghiệm thuộc đoạn $\left[0;1\right]$.
2. Cho hàm số $y=\dfrac{x+2}{x+1}$ có đồ thị $\left(\mathscr{C}\right)$. Tìm điểm $M$ thuộc $\left(\mathscr{C}\right)$ sao cho tiếp tuyến của $\left(\mathscr{C}\right)$ tại $M$ tạo với hai trục tọa độ một tam giác vuông cân.

Tam giác $HPS$ đều, cạnh $PS=a\sqrt{2}$. $S_{HPS}$ bằng

	$a^2\dfrac{\sqrt{3}}{4}$
	$a^2\dfrac{\sqrt{6}}{4}$
	$a^2\dfrac{\sqrt{3}}{2}$
	$a^2\dfrac{\sqrt{6}}{2}$

Tam giác $ABC$ có độ dài ba cạnh lần lượt là $21$cm, $17$cm và $10$cm. Tính diện tích tam giác.

	$S=16\text{ cm}^2$
	$S=24\text{ cm}^2$
	$S=48\text{ cm}^2$
	$S=84\text{ cm}^2$

Tam giác $ABC$ vuông cân tại $B$, có cạnh $AB=2a$. Phát biểu nào sau đây không đúng?

	$S=\dfrac{a^2}{2}$
	$\widehat{A}=\widehat{C}=45^\circ$
	$AB=BC=2a$
	$S=2a^2$