Tính diện tích $S$ của hình phẳng giới hạn bởi đồ thị hàm số $y=\cos{x}+2$, trục hoành và các đường thẳng $x=0$, $x=\dfrac{\pi}{4}$.

	$S=\dfrac{\pi}{2}-\dfrac{\sqrt{2}}{2}$
	$S=\dfrac{\pi}{4}+\dfrac{7}{10}$
	$S=\dfrac{\pi}{2}+\dfrac{\sqrt{2}}{2}$
	$S=\dfrac{\pi}{4}+\dfrac{\sqrt{2}}{2}$

Cho hình phẳng $(D)$ giới hạn bởi đồ thị hàm số $y=\sqrt{x}$, hai đường thẳng $x=1$, $x=2$ và trục hoành. Tính thể tích khối tròn xoay tạo thành khi quay $(D)$ quanh trục hoành.

	$3\pi$
	$\dfrac{3}{2}$
	$\dfrac{3\pi}{2}$
	$\dfrac{2\pi}{3}$

Tính thể tích khối tròn xoay được tạo bởi hình phẳng giới hạn bởi ba đường $y=\sqrt{x}$, $y=2-x$ và $y=0$ quanh trục $Ox$.

	$\dfrac{3\pi}{2}$
	$\dfrac{5\pi}{6}$
	$\pi$
	$\dfrac{2\pi}{3}$

Thể tích của khối tròn xoay tạo thành khi quay hình phẳng $D$ giới hạn bởi các đường $y=\sqrt{x-1}$, trục hoành, $x=2$ và $x=5$ quanh trục $Ox$ bằng

	$\displaystyle\int\limits_{2}^{5}(x-1)\mathrm{\,d}x$
	$\displaystyle\int\limits_{2}^{5}\sqrt{x-1}\mathrm{\,d}x$
	$\pi\displaystyle\int\limits_{2}^{5}(x-1)\mathrm{\,d}x$
	$\pi^2\displaystyle\int\limits_{2}^{5}(x-1)\mathrm{\,d}x$

Tính thể tích $V$ của vật tròn xoay tạo thành khi quay hình phẳng $(H)$ giới hạn bởi các đường $y=x^2$ và $y=\sqrt{x}$ quanh trục $Ox$.

	$V=\dfrac{3\pi}{10}$
	$V=\dfrac{\pi}{10}$
	$V=\dfrac{7\pi}{10}$
	$V=\dfrac{9\pi}{10}$

Gọi $(H)$ là hình phẳng tạo bởi đồ thị hàm số $y=\sqrt{x^3-x^2-2x}$ và trục hoành. Khi cho $(H)$ quay quanh trục hoành, ta được khối tròn xoay có thể tích là

	$\dfrac{13\pi}{6}$
	$\dfrac{9\pi}{4}$
	$\dfrac{5\pi}{12}$
	$\dfrac{8\pi}{3}$

Cho hình phẳng giới hạn bởi đồ thị các hàm số $y=\sqrt{x}$, đường thẳng $y=2-x$ và trục hoành (phần gạch chéo trong hình vẽ).

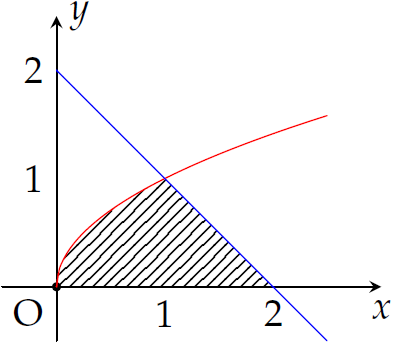
Thể tích của khối tròn xoay sinh bởi hình phẳng trên khi quay quanh trục $Ox$ bằng

	$\dfrac{5\pi}{4}$
	$\dfrac{4\pi}{3}$
	$\dfrac{7\pi}{6}$
	$\dfrac{5\pi}{6}$

Gọi $V$ là thể tích của khối tròn xoay thu được khi quay hình thang cong giới hạn bởi đồ thị hàm số $y=\sin x$, trục $Ox$, trục $Oy$ và đường thẳng $x=\dfrac{\pi}{2}$ xung quanh trục $Ox$. Mệnh đề nào dưới đây đúng?

	$V=\displaystyle\int\limits_{0}^{\tfrac{\pi}{2}}\sin^2x\mathrm{\,d}x$
	$V=\displaystyle\int\limits_{0}^{\tfrac{\pi}{2}}\sin x\mathrm{\,d}x$
	$V=\pi\displaystyle\int\limits_{0}^{\tfrac{\pi}{2}}\sin^2x\mathrm{\,d}x$
	$V=\pi\displaystyle\int\limits_{0}^{\tfrac{\pi}{2}}\sin x\mathrm{\,d}x$

Thể tích khối tròn xoay có được khi quay quanh trục $Ox$ hình phẳng giới hạn bởi các đường $y=\sqrt{x}$, $y=0$, $x=0$, $x=1$ bằng

	$V=\dfrac{\pi}{2}$
	$V=\dfrac{2\pi}{3}$
	$V=\dfrac{2}{3}$
	$V=\dfrac{1}{2}$

Cho hàm số $y=\sqrt{\dfrac{1-\cos x}{1-\sin x}}$. Tập xác định của hàm số là

	$\mathbb{R}\setminus\{\pi+k\pi,\,k\in\mathbb{Z}\}$
	$\mathbb{R}\setminus\left\{\dfrac{\pi}{2}+k2\pi,\,k\in\mathbb{Z}\right\}$
	$\{k2\pi,\,k\in\mathbb{Z}\}$
	$\mathbb{R}\setminus\{k\pi,\,k\in\mathbb{Z}\}$

Tính thể tích $V$ của vật thể giới hạn bởi hai mặt phẳng $x=0,\,x=\pi$. Biết rằng thiết diện của vật thể cắt bởi mặt phẳng vuông góc với $Ox$ tại điểm có hoành độ $x\,(0\leq x\leq\pi)$ là một tam giác vuông cân có cạnh huyền bằng $\sin x+2$.

	$\dfrac{7\pi}{6}+1$
	$\dfrac{9\pi}{8}+1$
	$\dfrac{7\pi}{6}+2$
	$\dfrac{9\pi}{8}+2$

Công thức tính thể tích vật thể tròn xoay thu được khi cho hình phẳng (phần gạch sọc của hình vẽ) giới hạn bởi các đường $y=\sqrt{x+2}$, $Ox$, $x=1$ quay xung quanh trục $Ox$ là

	$\pi\displaystyle\displaystyle\int\limits_{-2}^{1}(x+2)\mathrm{d}x$
	$\pi\displaystyle\displaystyle\int\limits_{1}^{4}\sqrt[4]{x+2}\mathrm{d}x$
	$\pi\displaystyle\displaystyle\int\limits_{-2}^{1}\sqrt{x+2}\mathrm{d}x$
	$\pi\displaystyle\displaystyle\int\limits_{1}^{4}(x+2)\mathrm{d}x$

Cho $\displaystyle\displaystyle\int\limits_{\tfrac{\pi}{6}}^{\tfrac{\pi}{4}}\cos4x\cos x\mathrm{\,d}x=\dfrac{\sqrt{2}}{a}+\dfrac{b}{c}$ với $a,\,b,\,c$ là các số nguyên, $c< 0$ và $\dfrac{b}{c}$ tối giản. Tổng $a+b+c$ bằng

	$-77$
	$-17$
	$103$
	$43$

Tính tích phân $I=\displaystyle\displaystyle\int\limits_{0}^{\pi}x^2\cos2x\mathrm{d}x$ bằng cách đặt $\begin{cases}u=x^2\\ \mathrm{d}v=\cos2x\mathrm{d}x\end{cases}$. Mệnh đề nào dưới đây đúng?

	$I=\dfrac{1}{2}x^2\sin2x\bigg|_{0}^{\pi}-\displaystyle\displaystyle\int\limits_{0}^{\pi}x\sin2x\mathrm{d}x$
	$I=\dfrac{1}{2}x^2\sin2x\bigg|_{0}^{\pi}-2\displaystyle\displaystyle\int\limits_{0}^{\pi}x\sin2x\mathrm{d}x$
	$I=\dfrac{1}{2}x^2\sin2x\bigg|_{0}^{\pi}+2\displaystyle\displaystyle\int\limits_{0}^{\pi}x\sin2x\mathrm{d}x$
	$I=\dfrac{1}{2}x^2\sin2x\bigg|_{0}^{\pi}+\displaystyle\displaystyle\int\limits_{0}^{\pi}x\sin2x\mathrm{d}x$

Tích phân $f\left(x\right)=\displaystyle\displaystyle\int\limits_{0}^{\tfrac{\pi}{3}}\cos x\mathrm{d}x$ bằng

	$\dfrac{1}{2}$
	$\dfrac{\sqrt{3}}{2}$
	$-\dfrac{\sqrt{3}}{2}$
	$-\dfrac{1}{2}$

Cho hình phẳng $A$ giới hạn bởi đồ thị hai hàm số $y=\sqrt{x}$ và $y=\dfrac{1}{2}x$ (phần tô đậm trong hình vẽ).

Tính thể tích $V$ khối tròn xoay tạo thành khi quay hình $A$ xung quanh trục $Ox$.

	$V=\dfrac{8}{3}\pi$
	$V=\dfrac{8}{5}\pi$
	$V=0,533$
	$V=0,53\pi$

Cho hình phẳng $D$ giới hạn bởi các đường $y=x+2$, $y=0$, $x=1$ và $x=3$. Tính thể tích $V$ của khối tròn xoay tạo thành khi quay hình $D$ xung quanh trục $Ox$.

	$V=\dfrac{98}{3}$
	$V=8\pi$
	$V=\dfrac{98\pi}{3}$
	$V=\dfrac{98\pi^2}{3}$

Gọi $D$ là hình phẳng giới hạn bởi đồ thị của hàm số $y=f(x)$ liên tục trên đoạn $[a;b]$, trục hoành và hai đường thẳng $x=a$, $x=b$. Thể tích $V$ của khối tròn xoay tạo thành khi quay hình $D$ xung quanh trục $Ox$ được tính theo công thức nào dưới đây?

	$V=\pi^2\displaystyle\displaystyle\int\limits_a^b f(x)\mathrm{\,d}x$
	$V=\pi\displaystyle\displaystyle\int\limits_a^b f^2(x)\mathrm{\,d}x$
	$V=\left(\pi\displaystyle\displaystyle\int\limits_a^b f(x)\mathrm{\,d}x\right)^2$
	$V=2\pi\displaystyle\displaystyle\int\limits_a^b f^2(x)\mathrm{\,d}x$

Cho hình phẳng $\mathscr{D}$ giới hạn bởi đồ thị hàm số $y=2x-x^2$ và trục $Ox$. Thể tích của khối tròn xoay được tạo thành khi quay $\mathscr{D}$ quanh trục $Ox$ bằng

	$\dfrac{256\pi}{15}$
	$\dfrac{64\pi}{15}$
	$\dfrac{16\pi}{15}$
	$\dfrac{4\pi}{3}$

Cho hình phẳng $\left(\mathscr{D}\right)$ giới hạn bởi đồ thị hàm số $y=\sqrt{x}$, hai đường thẳng $x=1$, $x=2$ và trục hoành. Tính thể tích khối tròn xoay tạo thành khi quay $\left(\mathscr{D}\right)$ quanh trục hoành.

	$3\pi$
	$\dfrac{3}{2}$
	$\dfrac{2\pi}{3}$
	$\dfrac{3\pi}{2}$