Số phức nào sau đây là số thuần ảo?
| \(z=3\mathrm{i}\) | |
| \(z=\sqrt{3}+\mathrm{i}\) | |
| \(z=-2+3\mathrm{i}\) | |
| \(z=-2\) |
Mệnh đề nào sau đây sai?
| Số phức \(z=2019\mathrm{i}\) là số thuần ảo | |
| Số \(2019\mathrm{i}\) không phải số thuần ảo | |
| Số phức \(z=5-3\mathrm{i}\) có phần thực bằng \(5\), phần ảo bằng \(-3\) | |
| Điểm \(M(-1;2)\) là điểm biểu diễn số phức \(z=-1+2\mathrm{i}\) |
Tìm số phức $z$ thỏa mãn $|z|=2$ và $z$ là số thuần ảo.
Có bao nhiêu số phức $z$ thỏa mãn $|z|=\sqrt{2}$ và $(z+2i)\left(\overline{z}-2\right)$ là số thuần ảo?
| $1$ | |
| $0$ | |
| $2$ | |
| $4$ |
Cho số phức \(z=(2m-1)+(m^2-4)i\), \(m\in\mathbb{R}\). Tìm \(m\) để số phức \(z\) là số thuần ảo.
| \(m=2,\,m=-2\) | |
| \(m=2\) | |
| \(m=-\dfrac{1}{2}\) | |
| \(m=\dfrac{1}{2}\) |
Cho \(z\) là một số thuần ảo khác \(0\). Mệnh đề nào sau đây đúng?
| \(\overline{z}\) là số thực | |
| Phần ảo của \(z\) bằng \(0\) | |
| \(z=\overline{z}\) | |
| \(z+\overline{z}=0\) |
Cho số phức \(z\) thỏa mãn $$z=\dfrac{(1+i)(2+i)}{1-i}+\dfrac{(1-i)(2-i)}{1+i}.$$Trong các kết luận sau, kết luận nào đúng?
| \(z=\overline{z}\) | |
| \(z\) là số thuần ảo | |
| \(|z|=4\) | |
| \(z=\dfrac{1}{\overline{z}}\) |
Tổng phần thực và phần ảo của số phức \(z=3-\mathrm{i}\) bằng
| \(2\) | |
| \(-1\) | |
| \(-2\) | |
| \(3\) |
Cho số phức \(z\) thỏa mãn \(\overline{z}=3+2\mathrm{i}\). Tìm phần thực và phần ảo của \(z\).
| \(3\) và \(2\) | |
| \(-3\) và \(2\) | |
| \(3\) và \(-2\) | |
| \(-3\) và \(-2\) |
Phần thực của số phức \(z=1+2\mathrm{i}\) là
| \(-1\) | |
| \(2\) | |
| \(1\) | |
| \(\mathrm{i}\) |
Phần ảo của số phức \(z=3-4\mathrm{i}\) là
| \(-4\) | |
| \(-4\mathrm{i}\) | |
| \(4\) | |
| \(4\mathrm{i}\) |
Phần thực và phần ảo của số phức \(z=1+2\mathrm{i}\) lần lượt là
| \(2\) và \(1\) | |
| \(1\) và \(2\mathrm{i}\) | |
| \(1\) và \(2\) | |
| \(1\) và \(\mathrm{i}\) |
Số phức \(z=-2\mathrm{i}\) có phần thực và phần ảo lần lượt là
| \(-2\) và \(0\) | |
| \(-2\mathrm{i}\) và \(0\) | |
| \(0\) và \(-2\) | |
| \(0\) và \(2\) |
Cho số phức \(z=a+b\mathrm{i}\). Khẳng định nào sau đây sai?
| \(z\) là số thuần ảo \(\Leftrightarrow a=0\) | |
| \(z\) là số thực \(\Leftrightarrow b=0\) | |
| \(z\) là số thuần ảo \(\Leftrightarrow\begin{cases}a=0\\ b\neq0\end{cases}\) | |
| \(z\) là số thuần ảo \(\Leftrightarrow\overline{z}\) là số thuần ảo |
Trên tập số phức, xét phương trình $z^2+az+b=0$ $(a,b\in\mathbb{R})$. Có bao nhiêu cặp số $(a,b)$ để phương trình đó có hai nghiệm phân biệt $z_1,\,z_2$ thỏa mãn $\big|z_1-2\big|=2$ và $\big|z_2+1-4i\big|=4$?
| $2$ | |
| $3$ | |
| $6$ | |
| $4$ |
Gọi $S$ là tập hợp các số phức $z=a+bi$ $(a,b\in\mathbb{R}$ thỏa mãn $\big|z+\overline{z}\big|+\big|z-\overline{z}\big|=6$ và $ab\le0$. Xét $z_1$ và $z_2$ thuộc $S$ sao cho $\dfrac{z_1-z_2}{-1+i}$ là số thực dương. Giá trị nhỏ nhất của biểu thức $\big|z_1+3i\big|+\big|z_2\big|$ bằng
| $3\sqrt{2}$ | |
| $3$ | |
| $3\sqrt{5}$ | |
| $3+3\sqrt{2}$ |
Gọi $z_1,\,z_2$ là hai nghiệm phức của phương trình $z^2-6z+14=0$ và $M,\,N$ lần lượt là điểm biểu diễn của $z_1,\,z_2$ trên mặt phẳng tọa độ. Trung điểm của đoạn $MN$ có tọa độ là
| $(3;7)$ | |
| $(-3;0)$ | |
| $(3;0)$ | |
| $(-3;7)$ |
Cho số phức $z=1-2i$. Phần ảo của số phức $\overline{z}$ bằng
| $-1$ | |
| $2$ | |
| $1$ | |
| $-2$ |
Cho hai số phức $z_1=2-i$ và $z_2=1+3i$. Phần thực của số phức $z_1-z_2$ bằng
| $3$ | |
| $-4$ | |
| $1$ | |
| $-1$ |
Điểm $M$ trong hình bên là điểm biểu diễn của số phức nào dưới đây?
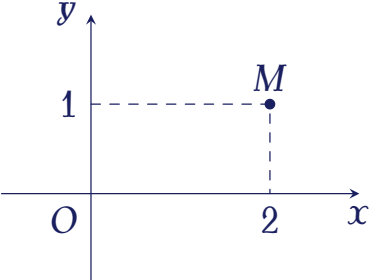
| $2-i$ | |
| $1+2i$ | |
| $1-2i$ | |
| $2+i$ |
