Một người gửi vào ngân hàng $100$ triệu với lãi suất $0,5$% một tháng, sau mỗi tháng lãi suất được nhập vào vốn. Hỏi sau một năm người đó rút tiền (cả vốn và lãi) thì tổng số tiền người đó nhận được là bao nhiêu?
| $100\cdot(1+12\cdot0,005)^{12}$ triệu đồng | |
| $100\cdot1,005$ triệu đồng | |
| $100\cdot1,005^{12}$ triệu đồng | |
| $100\cdot1,05^{12}$ triệu đồng |
Anh X muốn mua một chiếc xe máy Yamaha Exciter 150i giá \(47.500.000\) đồng của cửa hàng Phú Tài nhưng vì chưa đủ tiền nên anh X đã quyết định mua theo hình thức như sau: trả trước \(25\) triệu đồng và trả góp trong \(12\) tháng, với lãi suất \(0,6\%\)/tháng. Hỏi mỗi tháng, anh X sẽ phải trả cho cửa hàng Phú Tài số tiền là bao nhiêu? (quy tròn đến hàng đơn vị).
| \(2.014.546\) đồng | |
| \(1.948.000\) đồng | |
| \(2.014.545\) đồng | |
| \(1.948.927\) đồng |
Một người gửi tiết kiệm linh hoạt của ngân hàng cho con với số tiền là \(500.000.000\) đồng, lãi suất \(7\%\)/năm. Biết rằng người ấy không lấy lãi hàng năm theo định kỳ sổ tiết kiệm. Hỏi sau \(18\) năm, số tiền người ấy nhận về là bao nhiêu? (Biết rằng theo định kỳ rút tiền hàng năm, nếu không lấy lải thì số tiền sẽ được nhập vào thành tiền gốc và sổ tiết kiệm sẽ chuyển thành kỳ hạn \(1\) năm tiếp theo và lãi suất không thay đổi trong \(18\) năm).
| \(1.689.966.000\) đồng | |
| \(2.639.636.000\) đồng | |
| \(1.669.266.000\) đồng | |
| \(3.689.966.000\) đồng |
Một người gửi tiết kiệm số tiền \(80\) triệu đồng với lãi suất \(6,9\%\)/năm. Biết rằng tiền lãi hàng năm được nhập vào tiền gốc. Hỏi sau đúng \(5\) năm người đó rút được cả gốc và lãi số tiền gần với con số nào sau đây?
| \(105,370\) triệu đồng | |
| \(107,667\) triệu đồng | |
| \(111,680\) triệu đồng | |
| \(116,570\) triệu đồng |
Để đầu tư dự án trồng rau sạch theo công nghệ mới, bác Năm đã làm hợp đồng xin vay vốn ngân hàng số tiền \(100\) triệu đồng với lãi suất \(x\%\) mỗi năm. Điều kiện kèm theo của hợp đồng là số tiền lãi năm trước sẽ được tính làm vốn để sinh lãi cho năm sau. Sau hai năm thành công với dự án rau sạch của mình, bác Năm đã thanh toán hợp đồng ngân hàng số tiền làm tròn là \(129.512.000\) đồng. Khẳng định nào sau đây đúng?
| \(x=13\) | |
| \(x=15\) | |
| \(x=12\) | |
| \(x=14\) |
Một người gửi tiết kiệm số tiền \(80.000.000\) đồng với lãi suất \(6,9\%\)/năm. Biết rằng tiền lãi hàng năm được nhập vào tiền gốc, hỏi sau đúng \(5\) năm người đó rút được cả gốc lẫn lãi với số tiền gần với con số nào nhất sau đây?
| \(116.570.000\) đồng | |
| \(107.667.000\) đồng | |
| \(105.370.000\) đồng | |
| \(111.680.000\) đồng |
Ông Bình gửi số tiền \(58\) triệu đồng vào một ngân hàng theo hình thức lãi kép và ổn định trong \(9\) tháng thì lãnh được \(61.758.000\) đồng. Hỏi lãi suất ngân hàng mỗi tháng là bao nhiêu, biết rằng lãi suất không thay đổi trong suốt thời gian gửi?
| \(0,8\%\) | |
| \(0,6\%\) | |
| \(0,7\%\) | |
| \(0,5\%\) |
Một khu rừng có trữ lượng gỗ \(4\cdot10^5\text{m}^3\). Biết tốc độ sinh trưởng của các cây ở khu rừng đó là \(4\%\) mỗi năm. Hỏi sau \(5\) năm, khu rừng đó sẽ có khoảng bao nhiêu m\(^3\) gỗ?
| \(35\cdot10^5\text{m}^3\) | |
| \(4,8666\cdot10^5\text{m}^3\) | |
| \(2016\cdot10^3\text{m}^3\) | |
| \(125\cdot10^7\text{m}^3\) |
Để dự báo dân số của một quốc gia, người ta sử dụng công thức \(S=A\mathrm{e}^{nr}\); trong đó \(A\) là dân số của năm lấy làm mốc tính, \(S\) là dân số sau \(n\) năm, \(r\) là tỉ lệ tăng dân số hàng năm. Năm \(2017\), dân số Việt Nam là \(93.671.600\) người (Tổng cục Thống kê, Niên giám Thống kê năm \(2017\), Nhà xuất bản Thống kê, Tr. \(79\)). Giả sử tỉ lệ tăng dân số hàng năm không đổi là \(0,81\%\) dự báo dân số Việt Nam năm \(2035\) là bao nhiêu người (kết quả làm tròn đến chữ số hàng trăm)?
| \(109.256.100\) | |
| \(108.374.700\) | |
| \(107.500.500\) | |
| \(108.311.100\) |
Việt Nam là quốc gia nằm ở phía Đông bán đảo Đông Dương thuộc khu vực Đông Nam Á. Với dân số ước tính \(93,7\) triệu dân vào đầu năm 2018, Việt Nam là quốc gia đông dân thứ \(15\) trên thế giới và là quốc gia đông dân thứ \(8\) ở châu Á, tỉ lệ tăng dân số hàng năm \(1,2\%\). Giả sử rằng tỉ lệ tăng dân số từ năm 2018 đến năm 2030 không thay đổi thì dân số nước ta đầu năm 2030 khoảng bao nhiêu?
| \(118,12\) triệu dân | |
| \(106,12\) triệu dân | |
| \(128,12\) triệu dân | |
| \(108,12\) triệu dân |
Một khu rừng có trữ lượng gỗ \(4\cdot10^5\) mét khối. Biết tốc độ sinh trưởng của các cây trong rừng đó là \(4\%\) mỗi năm. Hỏi sau \(10\) năm khu rừng đó có số mét khối gỗ gần nhất với số nào sau đây?
| \(5,9\cdot10^5\) | |
| \(5,92\cdot10^5\) | |
| \(5,93\cdot10^5\) | |
| \(5,94\cdot10^5\) |
Ông An gửi số tiền $58$ triệu đồng vào một ngân hàng theo hình thức lãi kép, sau $9$ tháng thì nhận về được $61758000$ đồng. Biết rằng lãi suất không thay đổi trong thời gian gửi. Lãi suất hàng tháng của ngân hàng gần nhất với giá trị nào dưới đây?
| $0,7$% | |
| $0,8$% | |
| $0,6$% | |
| $0,5$% |
Ông Bình làm lan can ban công ngôi nhà của mình bằng một tấm kính cường lực. Tấm kính đó là một phần của mặt xung quanh của một hình trụ như hình bên.
Biết giá tiền của $1\text{ m}^2$ kính như trên là $1.500.000$ đồng. Hỏi số tiền (làm tròn đến hàng nghìn) mà ông Bình mua tấm kính trên là bao nhiêu?
| $23.591.000$ đồng | |
| $36.173.000$ đồng | |
| $9.437.000$ đồng | |
| $4.718.000$ đồng |
Một người gửi tiết kiệm với lãi suất \(5\)%/năm và lãi hàng năm được nhập vào vốn. Sau ít nhất bao nhiêu năm thì người đó nhận được số tiền lớn hơn \(150\)% số tiền gửi ban đầu?
| \(8\) năm | |
| \(10\) năm | |
| \(9\) năm | |
| \(11\) năm |
Một người gửi số tiền \(50\) triệu đồng vào một ngân hàng với lãi suất \(8,4\%\)/năm. Cứ mỗi năm, số tiền lãi sẽ được nhập vào vốn ban đầu để tính lãi cho năm tiếp theo. Người đó sẽ lĩnh được số tiền cả vốn lẫn lãi là \(80\) triệu sau \(n\) năm. Hỏi nếu trong khoảng thời gian này người đó không rút tiền và lãi suất không thay đổi thì \(n\) gần nhất với số nào sau đây?
| \(4\) | |
| \(5\) | |
| \(6\) | |
| \(7\) |
Bình Định có câu ca dao:
"Cưới nàng đôi nón Gò Găng
Xấp lãnh An Thái một khăn trầu nguồn."

Nói đến câu ca dao này là nói đến một làng nghề truyền thống có hàng trăm năm tuổi của thị xã An Nhơn, tỉnh Bình Định - làng nghề làm nón lá Gò Găng. Nhân kỷ niệm 10 năm được công nhận thị xã, thị xã An Nhơn lên kế hoạch làm các mô hình biểu tượng làng nghề truyền thống trên địa bàn, trong đó có mô hình chiếc nón lá Gò Găng. Chiếc nón có bán kính đáy \(1\) mét và chiều cao \(1,5\) mét, khung thép dùng làm đường tròn đáy và \(10\) đường nối từ đỉnh của nón đến đường tròn đáy có giá thành \(40.000\) đồng/mét, là của cây lá nón Licuala Fatoua Becc dùng để làm mặt nón có giá thành \(20.000\) đồng/mét vuông. Hỏi nếu bỏ qua diện tích các mép nối thì kinh phí để làm chiếc nón biểu tượng này là bao nhiêu?
| \(1.085.000\) đồng | |
| \(1.086.000\) đồng | |
| \(834.000\) đồng | |
| \(833.000\) đồng |
Một nhóm các chuyên gia y tế đang nghiên cứu và thử nghiệm độ chính xác của một bộ xét nghiệm COVID-19. Giả sử cứ sau $n$ lần thử nghiệm và điều chỉnh bộ xét nghiệm thì tỉ lệ chính xác của bộ xét nghiệm đó tuân theo công thức $S\left(n\right)=\dfrac{1}{1+2020\cdot10^{-0.01n}}$. Hỏi phải tiến hành ít nhất bao nhiêu lần thử nghiệm và điều chỉnh bộ xét nghiệm để đảm bảo tỉ lệ chính xác của bộ xét nghiệm đó đạt trên 90%?
| $426$ | |
| $425$ | |
| $428$ | |
| $427$ |
Một xưởng in có $15$ máy in được cài đặt tự động và giám sát bởi một kỹ sư, mỗi máy in có thể in được $30$ ấn phẩm trong một giờ, chi phí cài đặt và bảo dưỡng cho mỗi máy in cho một đơn hàng là $48.000$ đồng, chi phí trả cho kỹ sư giám sát là $24.000$ đồng/giờ. Đợt hàng này xưởng in nhận $6000$ ấn phẩm thì số máy in cần sử dụng để chi phí in ít nhất là
| $10$ máy | |
| $11$ máy | |
| $12$ máy | |
| $9$ máy |
Một mảnh vườn hình elip có độ dài trục lớn $8$m và độ dài trục nhỏ $6$m. Người ta cần trồng rau trên dải đất rộng $4$m như hình vẽ.
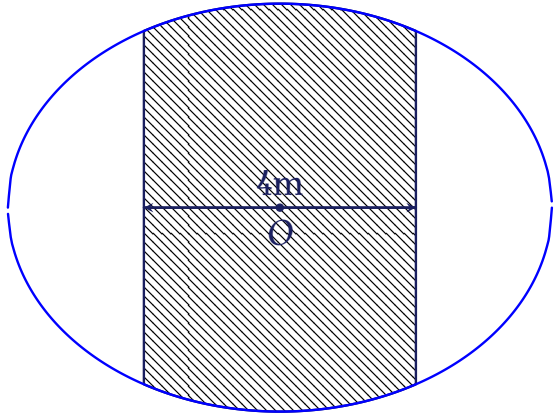
Hỏi cần bao nhiêu tiền để trồng rau trên dải đất đó, biết rằng kinh phí trồng rau là $70000$ đồng/m$^2$?
| $1.607.107$ đồng | |
| $803.553$ đồng | |
| $267.851$ đồng | |
| $2.638.938$ đồng |
Một bình đựng nước dạng hình nón (không có nắp đậy), đựng đầy nước. Biết rằng chiều cao của bình gấp $3$ lần bán kính đáy của nó. Người ta thả vào bình đó một khối trụ và đo được thể tích nước tràn ra ngoài là $\dfrac{16\pi}{9}\text{dm}^3$. Biết rằng một mặt của khối trụ nằm trên mặt đáy của hình nón và khối trụ có chiều cao bằng đường kính đáy của hình nón (hình vẽ).
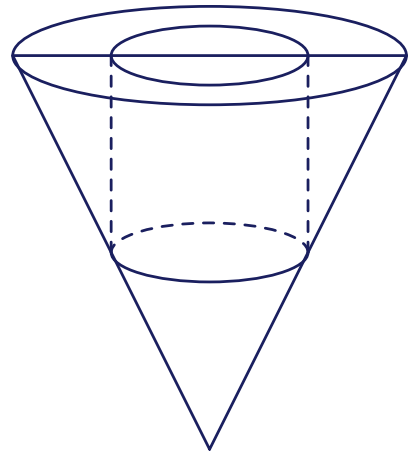
Tính bán kính đáy $R$ của bình nước.
| $R=4$dm | |
| $R=2$dm | |
| $R=3$dm | |
| $R=5$dm |
