Một người gửi vào ngân hàng $100$ triệu với lãi suất $0,5$% một tháng, sau mỗi tháng lãi suất được nhập vào vốn. Hỏi sau một năm người đó rút tiền (cả vốn và lãi) thì tổng số tiền người đó nhận được là bao nhiêu?
| $100\cdot(1+12\cdot0,005)^{12}$ triệu đồng | |
| $100\cdot1,005$ triệu đồng | |
| $100\cdot1,005^{12}$ triệu đồng | |
| $100\cdot1,05^{12}$ triệu đồng |
Ông An gửi số tiền $58$ triệu đồng vào một ngân hàng theo hình thức lãi kép, sau $9$ tháng thì nhận về được $61758000$ đồng. Biết rằng lãi suất không thay đổi trong thời gian gửi. Lãi suất hàng tháng của ngân hàng gần nhất với giá trị nào dưới đây?
| $0,7$% | |
| $0,8$% | |
| $0,6$% | |
| $0,5$% |
Anh X muốn mua một chiếc xe máy Yamaha Exciter 150i giá \(47.500.000\) đồng của cửa hàng Phú Tài nhưng vì chưa đủ tiền nên anh X đã quyết định mua theo hình thức như sau: trả trước \(25\) triệu đồng và trả góp trong \(12\) tháng, với lãi suất \(0,6\%\)/tháng. Hỏi mỗi tháng, anh X sẽ phải trả cho cửa hàng Phú Tài số tiền là bao nhiêu? (quy tròn đến hàng đơn vị).
| \(2.014.546\) đồng | |
| \(1.948.000\) đồng | |
| \(2.014.545\) đồng | |
| \(1.948.927\) đồng |
Một người gửi tiết kiệm với lãi suất \(5\)%/năm và lãi hàng năm được nhập vào vốn. Sau ít nhất bao nhiêu năm thì người đó nhận được số tiền lớn hơn \(150\)% số tiền gửi ban đầu?
| \(8\) năm | |
| \(10\) năm | |
| \(9\) năm | |
| \(11\) năm |
Ông An gửi vào ngân hàng \(60\) triệu đồng theo hình thức lãi kép. Lãi suất ngân hàng là \(8\)% một năm. Sau \(5\) năm ông An tiếp tục gửi vào thêm \(60\) triệu nữa. Hỏi sau \(10\) năm kể từ lần gửi đầu tiên, ông An đến rút toàn bộ tiền gốc và lãi thì được bao nhiêu, biết rằng lãi suất không thay đổi qua các năm ông gửi tiền?
| \(231,815\) (triệu đồng) | |
| \(197,201\) (triệu đồng) | |
| \(217,695\) (triệu đồng) | |
| \(190,271\) (triệu đồng) |
Một người gửi tiết kiệm linh hoạt của ngân hàng cho con với số tiền là \(500.000.000\) đồng, lãi suất \(7\%\)/năm. Biết rằng người ấy không lấy lãi hàng năm theo định kỳ sổ tiết kiệm. Hỏi sau \(18\) năm, số tiền người ấy nhận về là bao nhiêu? (Biết rằng theo định kỳ rút tiền hàng năm, nếu không lấy lải thì số tiền sẽ được nhập vào thành tiền gốc và sổ tiết kiệm sẽ chuyển thành kỳ hạn \(1\) năm tiếp theo và lãi suất không thay đổi trong \(18\) năm).
| \(1.689.966.000\) đồng | |
| \(2.639.636.000\) đồng | |
| \(1.669.266.000\) đồng | |
| \(3.689.966.000\) đồng |
Một người gửi tiết kiệm số tiền \(80\) triệu đồng với lãi suất \(6,9\%\)/năm. Biết rằng tiền lãi hàng năm được nhập vào tiền gốc. Hỏi sau đúng \(5\) năm người đó rút được cả gốc và lãi số tiền gần với con số nào sau đây?
| \(105,370\) triệu đồng | |
| \(107,667\) triệu đồng | |
| \(111,680\) triệu đồng | |
| \(116,570\) triệu đồng |
Để đầu tư dự án trồng rau sạch theo công nghệ mới, bác Năm đã làm hợp đồng xin vay vốn ngân hàng số tiền \(100\) triệu đồng với lãi suất \(x\%\) mỗi năm. Điều kiện kèm theo của hợp đồng là số tiền lãi năm trước sẽ được tính làm vốn để sinh lãi cho năm sau. Sau hai năm thành công với dự án rau sạch của mình, bác Năm đã thanh toán hợp đồng ngân hàng số tiền làm tròn là \(129.512.000\) đồng. Khẳng định nào sau đây đúng?
| \(x=13\) | |
| \(x=15\) | |
| \(x=12\) | |
| \(x=14\) |
Một người gửi tiết kiệm số tiền \(80.000.000\) đồng với lãi suất \(6,9\%\)/năm. Biết rằng tiền lãi hàng năm được nhập vào tiền gốc, hỏi sau đúng \(5\) năm người đó rút được cả gốc lẫn lãi với số tiền gần với con số nào nhất sau đây?
| \(116.570.000\) đồng | |
| \(107.667.000\) đồng | |
| \(105.370.000\) đồng | |
| \(111.680.000\) đồng |
Ông Bình gửi số tiền \(58\) triệu đồng vào một ngân hàng theo hình thức lãi kép và ổn định trong \(9\) tháng thì lãnh được \(61.758.000\) đồng. Hỏi lãi suất ngân hàng mỗi tháng là bao nhiêu, biết rằng lãi suất không thay đổi trong suốt thời gian gửi?
| \(0,8\%\) | |
| \(0,6\%\) | |
| \(0,7\%\) | |
| \(0,5\%\) |
Phương trình $3^{2x}-(m+1)3^x+m=0$ có đúng một nghiệm khi
| $m=0$ | |
| $m>0$ | |
| $m>0$, $m\neq1$ | |
| $m=1$ hoặc $m\leq0$ |
Tổng tất cả các nghiệm của phương trình $9^{x^2-2x-7}=3$ là
| $2$ | |
| $7$ | |
| $-7$ | |
| $4$ |
Cho phương trình $9^x-2\cdot3^{x+2}-1=0$. Đặt $t=3^x$, $t>0$, phương trình đã cho trở thành phương trình nào dưới đây?
| $2t^2-9t-2=0$ | |
| $t^2-9t-1=0$ | |
| $t^2-18t-1=0$ | |
| $9t^2-2t-9=0$ |
Phương trình $3^{1-x}=9$ có nghiệm là
| $x=-1$ | |
| $x=-2$ | |
| $x=1$ | |
| $x=2$ |
Có bao nhiêu giá trị nguyên của tham số $m\in(-10;100)$ để tồn tại các số thực dương $a,\,b,\,x,\,y$ thỏa mãn $a\neq1$, $b\neq1$ và $a^{2x}=b^y=(ab)^{x+my}$?
| $0$ | |
| $100$ | |
| $99$ | |
| $98$ |
Cho hàm số $f(x)=ax^3+bx^2+cx+d$ ($a\neq0$) có đồ thị là đường cong trong hình bên.
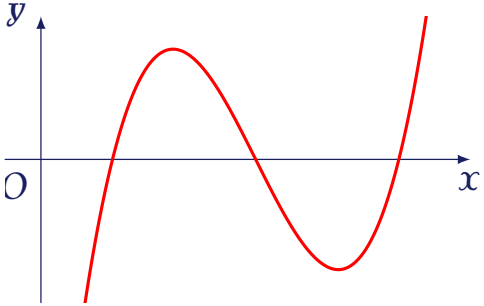
Số các giá trị nguyên của tham số $m\in(-2019;2023]$ để phương trình $4^{f(x)}-(m-1)2^{f(x)+1}+2m-3=0$ có đúng ba nghiệm là
| $2020$ | |
| $2019$ | |
| $2021$ | |
| $2022$ |
Nghiệm của phương trình $2^{x+1}=4$ là
| $x=3$ | |
| $x=1$ | |
| $x=2$ | |
| $x=0$ |
Nghiệm của phương trình $2^{2x-1}=8$ là
| $x=\dfrac{5}{2}$ | |
| $x=3$ | |
| $x=2$ | |
| $x=\dfrac{3}{2}$ |
Tìm nghiệm của phương trình $3^{x-1}=27$.
| $x=10$ | |
| $x=3$ | |
| $x=4$ | |
| $x=9$ |
Cho phương trình $9^x-2\cdot3^{x+2}-1=0$. Đặt $t=3^x$, $t>0$, phương trình đã cho trở thành phương trình nào dưới đây?
| $2t^2-9t-2=0$ | |
| $t^2-9t-1=0$ | |
| $t^2-18t-1=0$ | |
| $9t^2-2t-9=0$ |
