Tìm $m$ để phương trình $\dfrac{2\sin x+\cos x+1}{\sin x-2\cos x+3}=m$ có nghiệm.
| $\dfrac{1}{2}\leq m\leq2$ | |
| $m\geq2$ | |
| $m\leq-\dfrac{1}{2}$ | |
| $-\dfrac{1}{2}\leq m\leq2$ |
Cho $\displaystyle\displaystyle\int\limits_{\tfrac{\pi}{6}}^{\tfrac{\pi}{4}}\cos4x\cos x\mathrm{\,d}x=\dfrac{\sqrt{2}}{a}+\dfrac{b}{c}$ với $a,\,b,\,c$ là các số nguyên, $c< 0$ và $\dfrac{b}{c}$ tối giản. Tổng $a+b+c$ bằng
| $-77$ | |
| $-17$ | |
| $103$ | |
| $43$ |
Có bao nhiêu giá trị nguyên của tham số \(m\) thuộc khoảng \((-6;5)\) sao cho phương trình $$2\cos2x+4\sin x-m\sqrt{2}=0$$vô nghiệm?
| \(3\) | |
| \(2\) | |
| \(4\) | |
| \(5\) |
Cho \(\displaystyle\int\limits_{\tfrac{\pi}{6}}^{\tfrac{\pi}{2}}\dfrac{\cos x}{\sin x+1}\mathrm{\,d}x=a\ln2+b\ln3\) (\(a,\,b\in\mathbb{Z}\)). Khi đó, giá trị của \(a\cdot b\) là
| \(2\) | |
| \(-2\) | |
| \(-4\) | |
| \(3\) |
Cho \(\displaystyle\int\limits_{0}^{\tfrac{\pi}{2}}\dfrac{\cos x}{\left(\sin x\right)^2-5\sin x+6}\mathrm{\,d}x=a\ln\dfrac{4}{c}+b\), với \(a,\,b\) là các số hữu tỉ, \(c>0\). Tính tổng \(S=a+b+c\).
| \(S=3\) | |
| \(S=4\) | |
| \(S=0\) | |
| \(S=1\) |
Giá trị nào của \(a\) để $$\displaystyle\int\limits_{0}^{a}\left(3x^2+2\right)\mathrm{\,d}x=a^3+2?$$
| \(1\) | |
| \(2\) | |
| \(0\) | |
| \(3\) |
Cho \(a\) là số thực thỏa mãn \(|a|<2\) và \(\displaystyle\int\limits_a^2(2x+1)\mathrm{\,d}x=4\). Giá trị biểu thức \(1+a^3\) bằng
| \(0\) | |
| \(2\) | |
| \(1\) | |
| \(3\) |
Cho \(M\), \(N\) là các số thực, xét hàm số \(f(x)=M\sin\pi x+N\cos\pi x\) thỏa mãn \(f(1)=3\) và \(\displaystyle\int\limits_0^{\tfrac{1}{2}}f(x)\mathrm{\,d}x=-\dfrac{1}{\pi}\). Giá trị của \(f'\left(\dfrac{1}{4}\right)\) bằng
| \(\dfrac{5\pi\sqrt{2}}{2}\) | |
| \(-\dfrac{5\pi\sqrt{2}}{2}\) | |
| \(-\dfrac{\pi\sqrt{2}}{2}\) | |
| \(\dfrac{\pi\sqrt{2}}{2}\) |
Cho \(a,\,b\) là các số thực thỏa mãn \(\displaystyle\int\limits_0^1\dfrac{2abx+a+b}{(1+ax)(1+bx)}\mathrm{\,d}x=0\). Giá trị của \(S=ab+a+b\) bằng
| \(\left[\begin{array}{l}S=0\\ S=1\end{array}\right.\) | |
| \(\left[\begin{array}{l}S=-2\\ S=0\end{array}\right.\) | |
| \(\left[\begin{array}{l}S=1\\ S=-2\end{array}\right.\) | |
| \(\left[\begin{array}{l}S=-2\\ S=1\end{array}\right.\) |
Biết \(\displaystyle\int\limits_1^2{\dfrac{\mathrm{\,d}x}{4x^2-4x+1}}=\dfrac{1}{a}+\dfrac{1}{b}\) thì \(a,\,b\) là nghiệm của phương trình nào sau đây?
| \(x^2-5x+6=0\) | |
| \(x^2+4x-12=0\) | |
| \(2x^2-x-1=0\) | |
| \(x^2-9=0\) |
Cho \(I=\displaystyle\int\limits_0^{\tfrac{\pi}{4}}\tan^2x\mathrm{\,d}x=a-\dfrac{b\pi}{c}\) với \(a\), \(b\), \(c\) là các số nguyên dương, \(b\) và \(c\) nguyên tố cùng nhau. Giá trị của biểu thức \(T=\dfrac{a}{b}+2c\) là
| \(7\) | |
| \(5\) | |
| \(9\) | |
| \(3\) |
Tìm các giá trị của \(b\) sao cho \(\displaystyle\int\limits_0^b(2x-4)\mathrm{\,d}x=5\).
| \(\{-1;4\}\) | |
| \(\{5\}\) | |
| \(\{-1\}\) | |
| \(\{-1;5\}\) |
Cho tích phân \(\displaystyle\int\limits_0^{\tfrac{\pi}{2}} \left(4x-1+\cos x\right)\mathrm{\,d}x=\pi\left(\dfrac{\pi}{a}-\dfrac{1}{b}\right)+c\), \((a,b,c\in\mathbb{Q})\). Tính \(a-b+c\).
| \(\dfrac{1}{2}\) | |
| \(1\) | |
| \(-2\) | |
| \(\dfrac{1}{3}\) |
Tìm số thực \(m\) thỏa mãn $$\displaystyle 9+\int\limits_{0}^{1}{(2m^{2}x-6m)\mathrm{\,d}x}=0.$$
| \(m=1\) | |
| \(m=2\) | |
| \(m=3\) | |
| \(m=4\) |
Tìm giá trị của \(b\) để \(\displaystyle\int\limits_1^b(2x-6)\mathrm{\,d}x=0\).
| \(b=0\) hoặc \(b=1\) | |
| \(b=0\) hoặc \(b=3\) | |
| \(b=1\) hoặc \(b=5\) | |
| \(b=5\) hoặc \(b=0\) |
Cho hàm số $f(x)=ax^3+bx^2+cx+d$ ($a\neq0$) có đồ thị là đường cong trong hình bên.
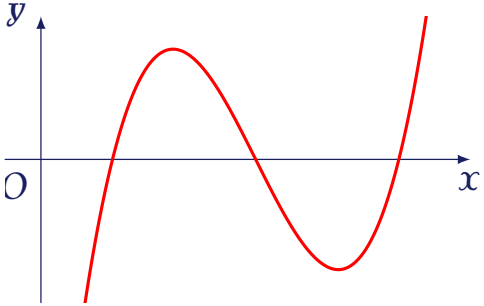
Số các giá trị nguyên của tham số $m\in(-2019;2023]$ để phương trình $4^{f(x)}-(m-1)2^{f(x)+1}+2m-3=0$ có đúng ba nghiệm là
| $2020$ | |
| $2019$ | |
| $2021$ | |
| $2022$ |
Cho hàm số $f(x)=x^3+ax^2+bx+c$ với $a,\,b,\,c$ là các số thực. Biết hàm số $g(x)=f(x)+f'(x)+f''(x)$ có hai giá trị cực trị là $-3$ và $6$. Diện tích hình phẳng giới hạn bởi các đường $y=\dfrac{f(x)}{g(x)+6}$ và $y=1$ bằng
| $2\ln3$ | |
| $\ln3$ | |
| $\ln18$ | |
| $2\ln2$ |
Tính thể tích $V$ của vật thể giới hạn bởi hai mặt phẳng $x=0,\,x=\pi$. Biết rằng thiết diện của vật thể cắt bởi mặt phẳng vuông góc với $Ox$ tại điểm có hoành độ $x\,(0\leq x\leq\pi)$ là một tam giác vuông cân có cạnh huyền bằng $\sin x+2$.
| $\dfrac{7\pi}{6}+1$ | |
| $\dfrac{9\pi}{8}+1$ | |
| $\dfrac{7\pi}{6}+2$ | |
| $\dfrac{9\pi}{8}+2$ |
Tính tích phân $I=\displaystyle\displaystyle\int\limits_{0}^{\tfrac{\pi}{4}}\sin x\mathrm{\,d}x$.
| $I=1-\dfrac{\sqrt{2}}{2}$ | |
| $I=-1+\dfrac{\sqrt{2}}{2}$ | |
| $I=-\dfrac{\sqrt{2}}{2}$ | |
| $I=\dfrac{\sqrt{2}}{2}$ |
Cho hàm số $f(x)$ liên tục trên $\mathbb{R}$ thỏa $f(x)=\sin x+2\displaystyle\int\limits_{0}^{\tfrac{\pi}{2}}\cos x\cdot f(x)\mathrm{\,d}x$. Giá trị $f\left(-\dfrac{\pi}{2}\right)$ bằng
| $-\pi$ | |
| $-1$ | |
| $-2$ | |
| $0$ |
