Đồ thị của hàm số \(y=x^2+4x+1\) là đường cong nào dưới đây?
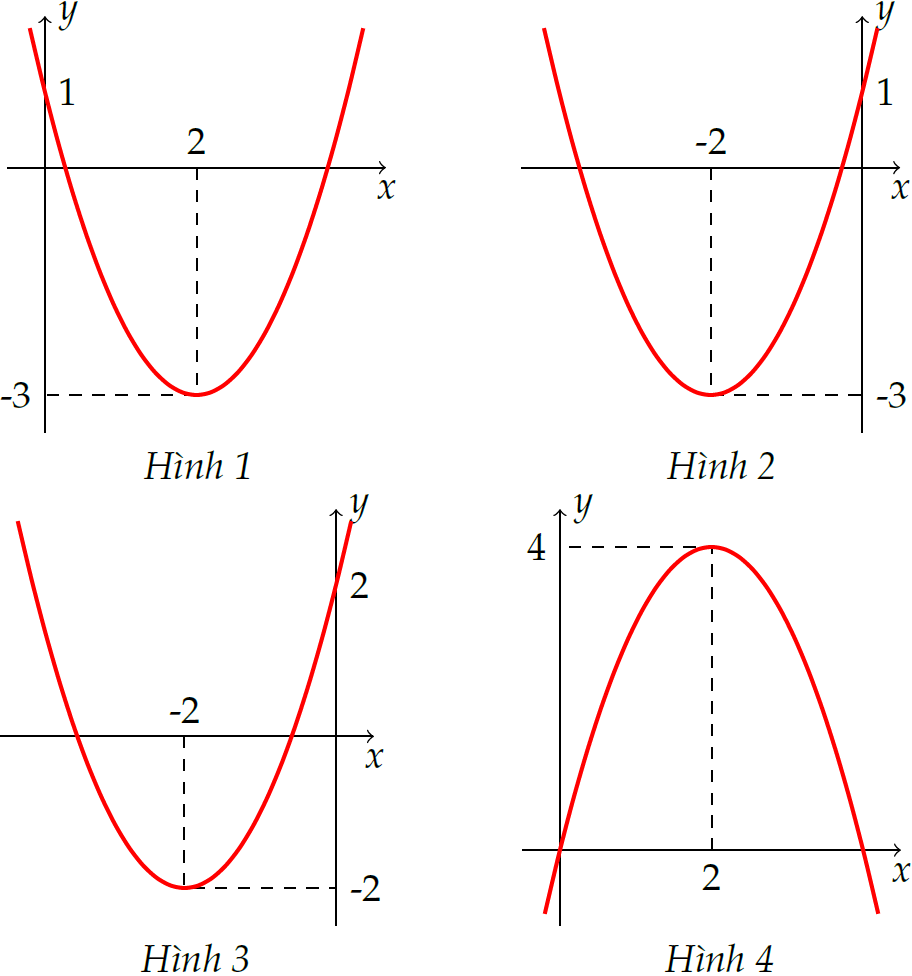
| Hình 1 | |
| Hình 2 | |
| Hình 3 | |
| Hình 4 |
Hàm số nào dưới đây có đồ thị như đường cong trong hình bên?
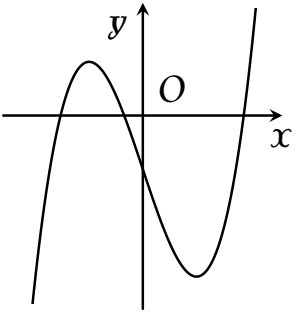
| $y=x^4-2x^2-1$ | |
| $y=\dfrac{x+1}{x-1}$ | |
| $y=x^3-3x-1$ | |
| $y=x^2+x-1$ |
Một chiếc cổng hình parabol dạng $y=-\dfrac{1}{2}x^2$ có chiều rộng chân cổng $d=8$m (như hình).
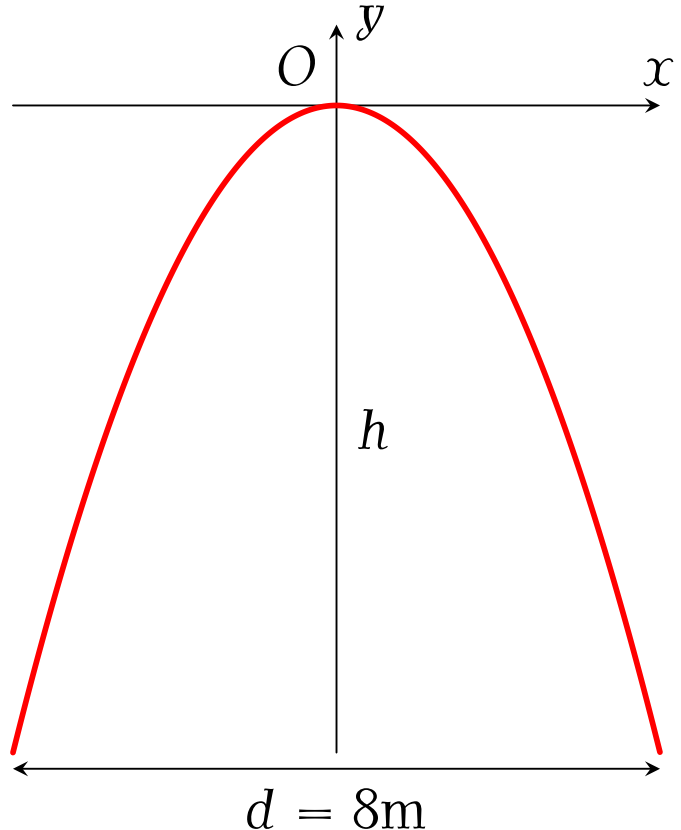
Hãy tính chiều cao $h$ của cổng.
| $h=8$m | |
| $h=9$m | |
| $h=7$m | |
| $h=5$m |
Một vật chuyển động trong $3$ giờ với vận tốc $v$ (km/h) phụ thuộc thời gian $t$ (h) có đồ thị là một phần của đường parabol với đỉnh $I(2;9)$ và trục đối xứng song song với trục tung (như hình vẽ).
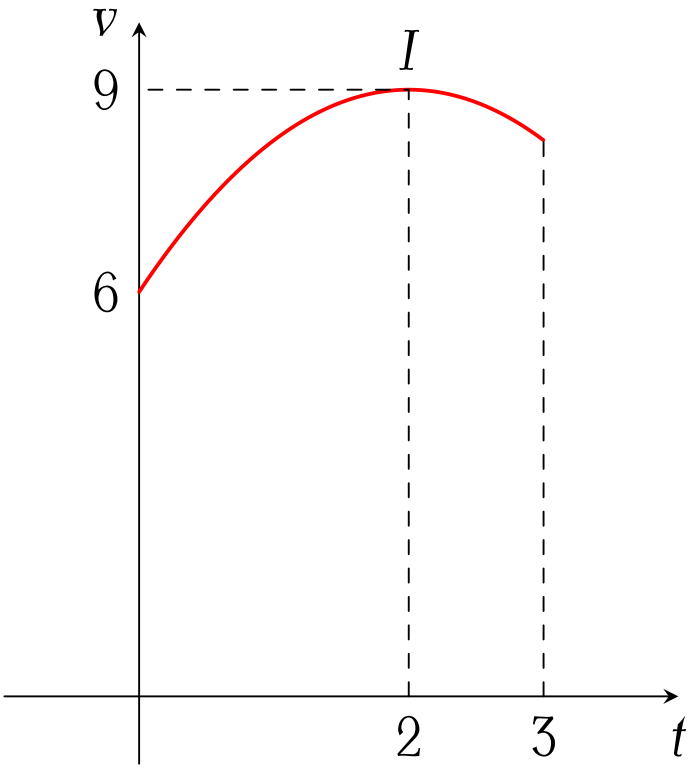
Vận tốc tức thời của vật tại thời điểm $2$ giờ $30$ phút sau khi vật bắt đầu chuyển động gần bằng giá trì nào nhất trong các giá trị sau:
| $8,7$ (km/h) | |
| $8,8$ (km/h) | |
| $8,6$ (km/h) | |
| $8,5$ (km/h) |
Cho hàm số $y=ax^2+bx+c$ có đồ thị như hình bên. Khẳng định nào sau đây là đúng?
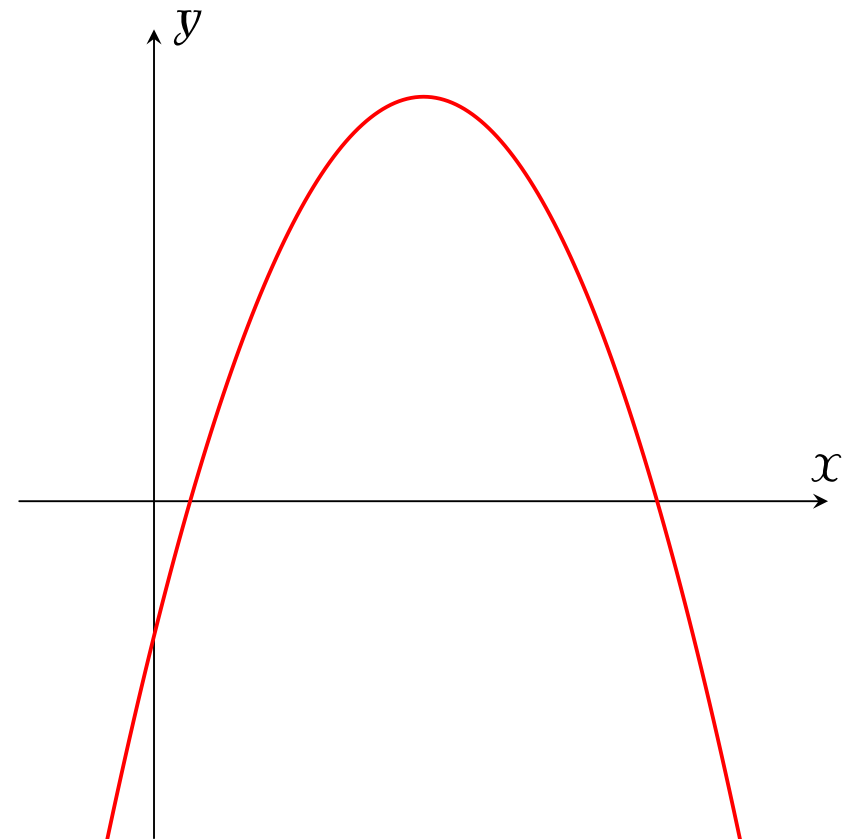
| $a>0,\,b>0,\,c<0$ | |
| $a>0,\,b<0,\,c>0$ | |
| $a<0,\,b>0,\,c<0$ | |
| $a<0,\,b>0,\,c>0$ |
Cho hàm số $y=ax^2+bx+c$ có đồ thị như hình bên. Khẳng định nào sau đây là đúng?
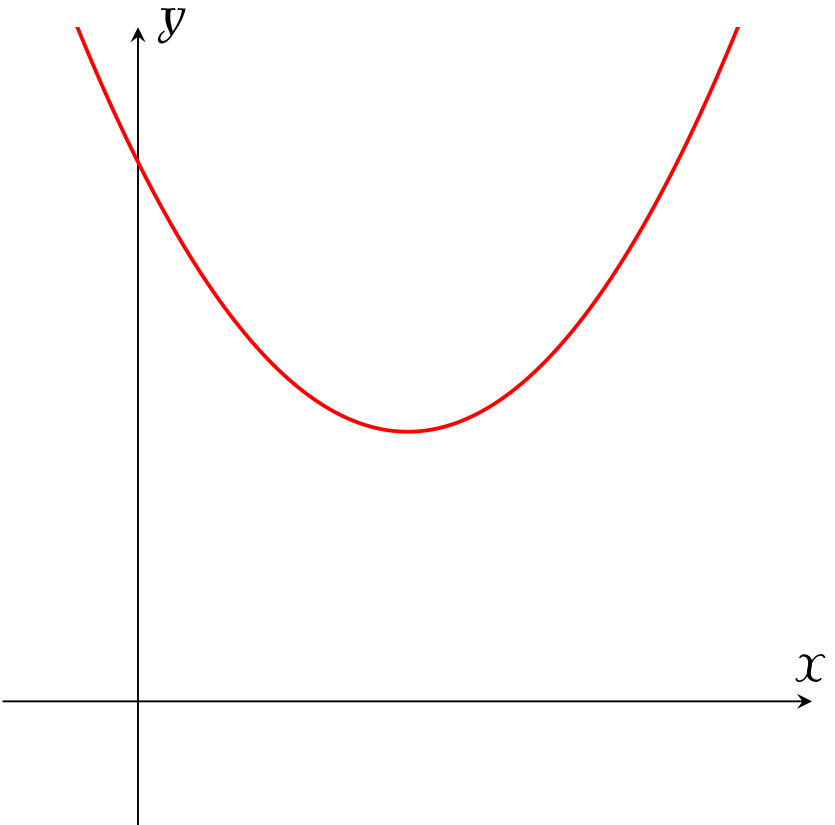
| $a>0,\,b<0,\,c<0$ | |
| $a>0,\,b<0,\,c>0$ | |
| $a>0,\,b>0,\,c>0$ | |
| $a<0,\,b<0,\,c>0$ |
Đồ thị trong hình bên là của hàm số nào sau đây?
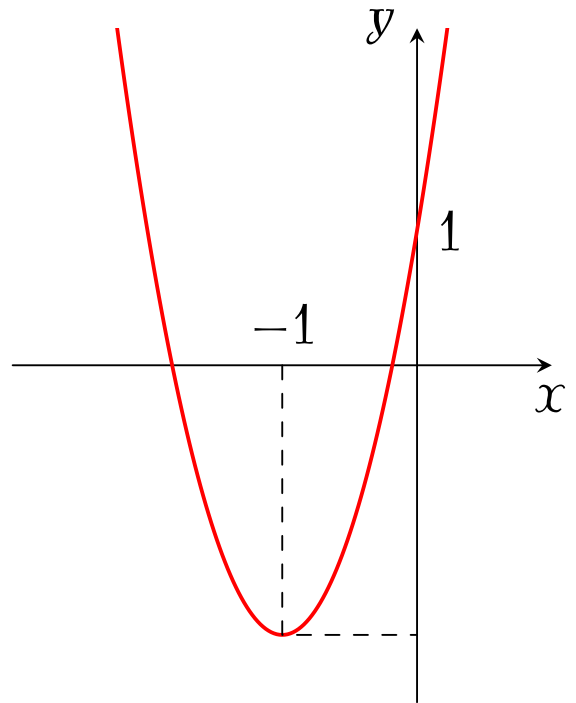
| $y=-3x^2-6x$ | |
| $y=3x^2+6x+1$ | |
| $y=x^2+2x+1$ | |
| $y=-x^2-2x+1$ |
Đồ thị trong hình bên là của hàm số nào sau đây?
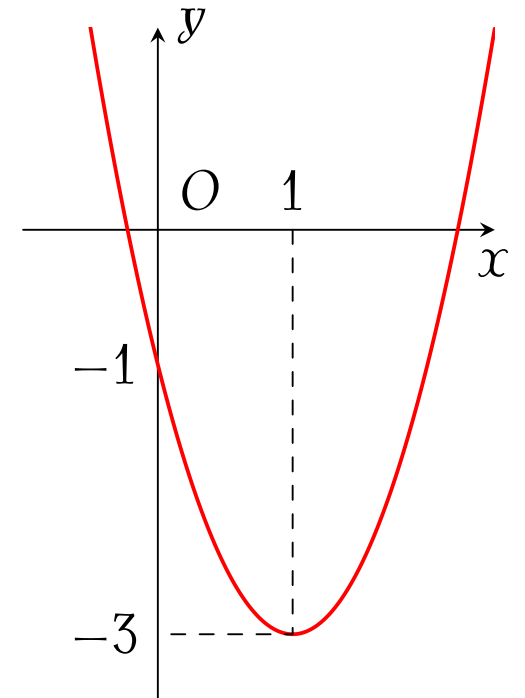
| $y=x^2-4x-1$ | |
| $y=2x^2-4x-1$ | |
| $y=-2x^2-4x-1$ | |
| $y=2x^2-4x+1$ |
Đồ thị trong hình bên là của hàm số nào sau đây?
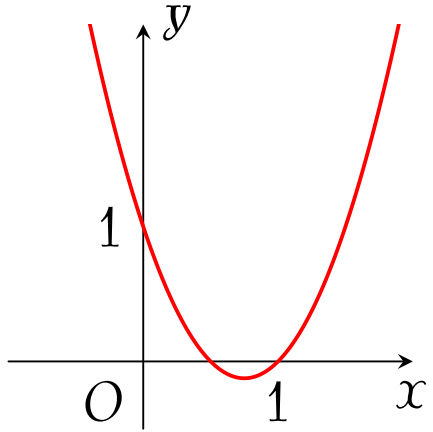
| $y=-x^2+3x-1$ | |
| $y=-2x^2+3x-1$ | |
| $y=2x^2-3x+1$ | |
| $y=x^2-3x+1$ |
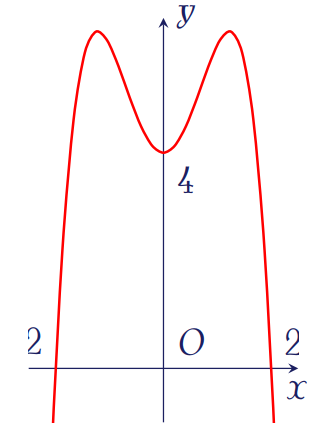
Đồ thị trong hình vẽ bên là của hàm số
| \(y=-x^2+x-4\) | |
| \(y=x^4-3x^2-4\) | |
| \(y=-x^3+2x^2+4\) | |
| \(y=-x^4+3x^2+4\) |
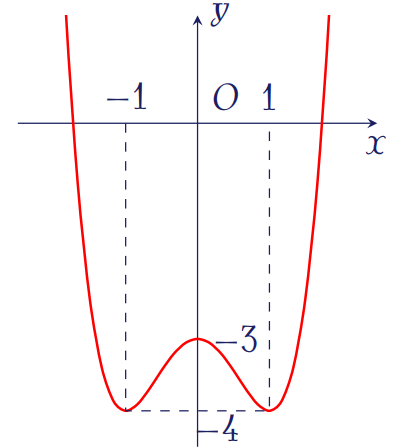
Đường cong trong hình vẽ bên là của hàm số nào sau đây?
| \(y=-x^3+x^2-2\) | |
| \(y=-x^4+3x^2-2\) | |
| \(y=x^4-2x^2-3\) | |
| \(y=-x^2+x-1\) |
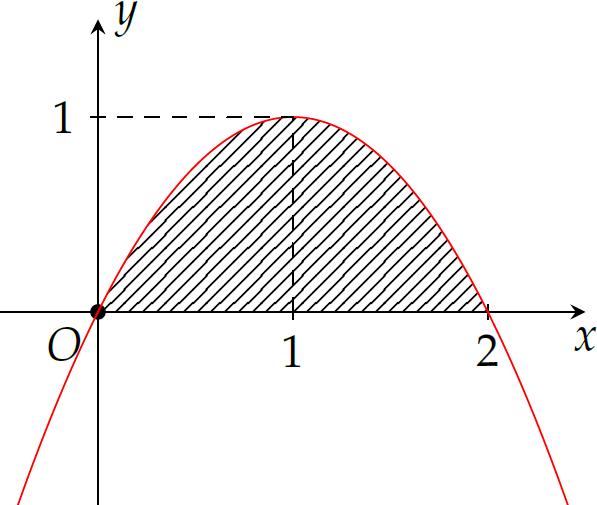
Cho hàm bậc hai \(y=f(x)\) có đồ thị như hình bên. Tính thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi đồ thị hàm số \(y=f(x)\) và \(Ox\) quanh \(Ox\).
| \(\dfrac{4\pi}{3}\) | |
| \(-\dfrac{12\pi}{15}\) | |
| \(\dfrac{16\pi}{15}\) | |
| \(\dfrac{16\pi}{5}\) |
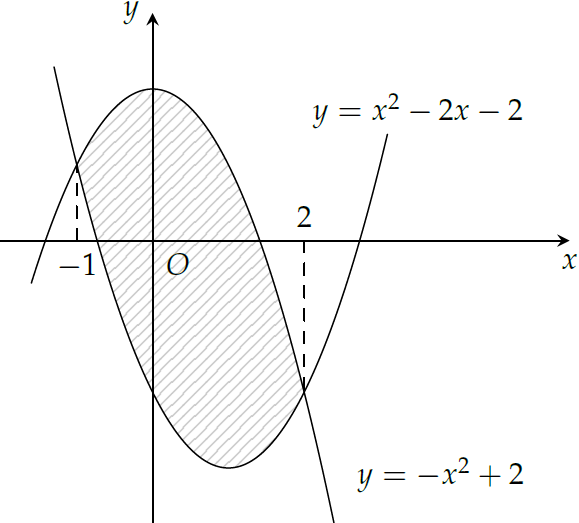
Diện tích phần hình phẳng được gạch chéo trong hình bên bằng
| \(\displaystyle\int\limits_{-1}^{2}{\left(-2x^2+2x+4\right)\mathrm{\,d}x}\) | |
| \(\displaystyle\int\limits_{-1}^{2}{\left(2x^2-2x-4\right)\mathrm{\,d}x}\) | |
| \(\displaystyle\int\limits_{-1}^{2}{\left(-2x^2-2x+4\right)\mathrm{\,d}x}\) | |
| \(\displaystyle\int\limits_{-1}^{2}{\left(2x^2+2x-4\right)\mathrm{\,d}x}\) |
Hình vẽ sau đây là đồ thị của hàm số nào?
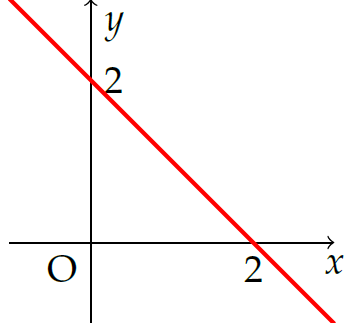
| \(y=2-x\) | |
| \(y=x-2\) | |
| \(y=2-2x\) | |
| \(y=1-2x\) |
Hình vẽ nào dưới đây là đồ thị của hàm số \(y=\dfrac{x}{2}-2\)?
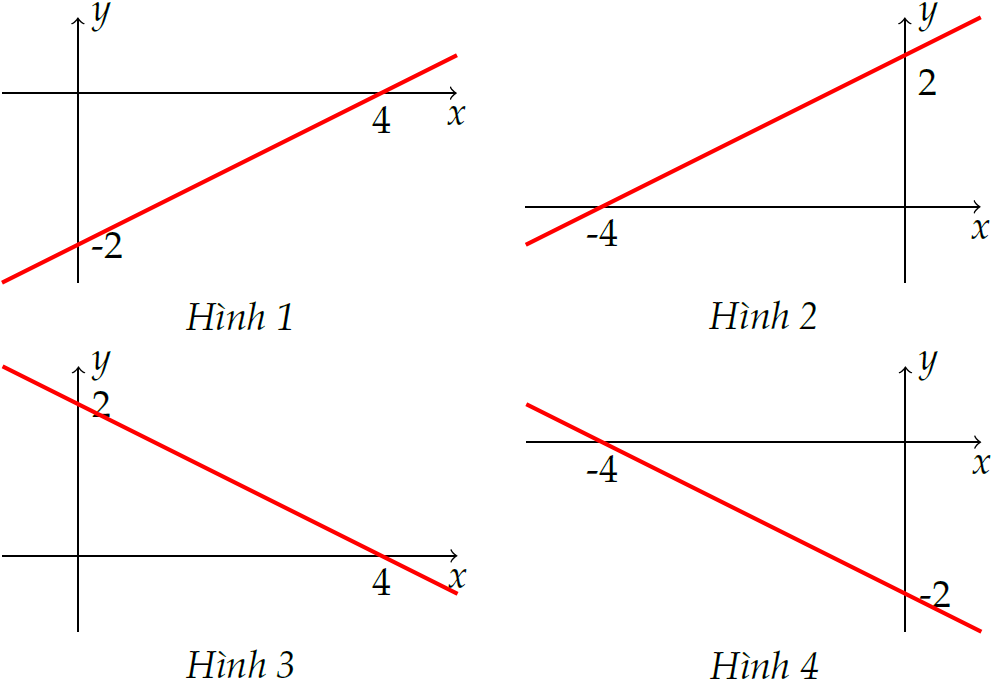
| Hình 1 | |
| Hình 2 | |
| Hình 3 | |
| Hình 4 |
Cho các hàm số \(y=\log_ax\), \(y=b^x\), \(y=c^x\) có đồ thị như hình vẽ.
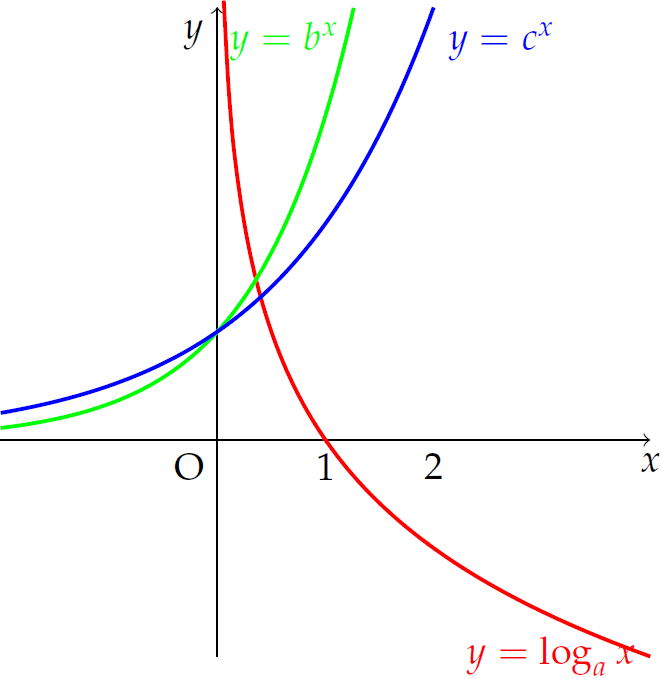
Mệnh đề nào dưới đây là đúng?
| \(b>c>a\) | |
| \(a>b>c\) | |
| \(b>a>c\) | |
| \(c>b>a\) |
Hình vẽ bên biểu diễn đồ thị của hai hàm số \(y=a^x\) và \(y=\log_bx\) với \(a,\,b\) là các số thực dương và \(b\neq1\).
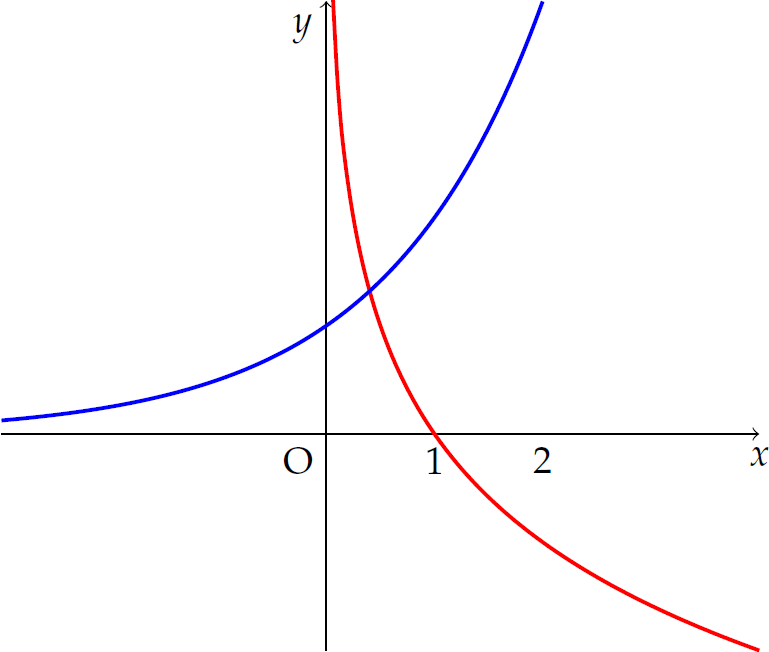
Mệnh đề nào dưới đây là đúng?
| \(\log_ab^2>0\) | |
| \(\log_ab<0\) | |
| \(\log_ab>0\) | |
| \(\log_ba>0\) |
Cho ba số thực dương \(a,\,b,\,c\) khác \(1\). Đồ thị hàm số \(y=a^x\), \(y=b^x\) và \(y=c^x\) được cho trong hình vẽ.
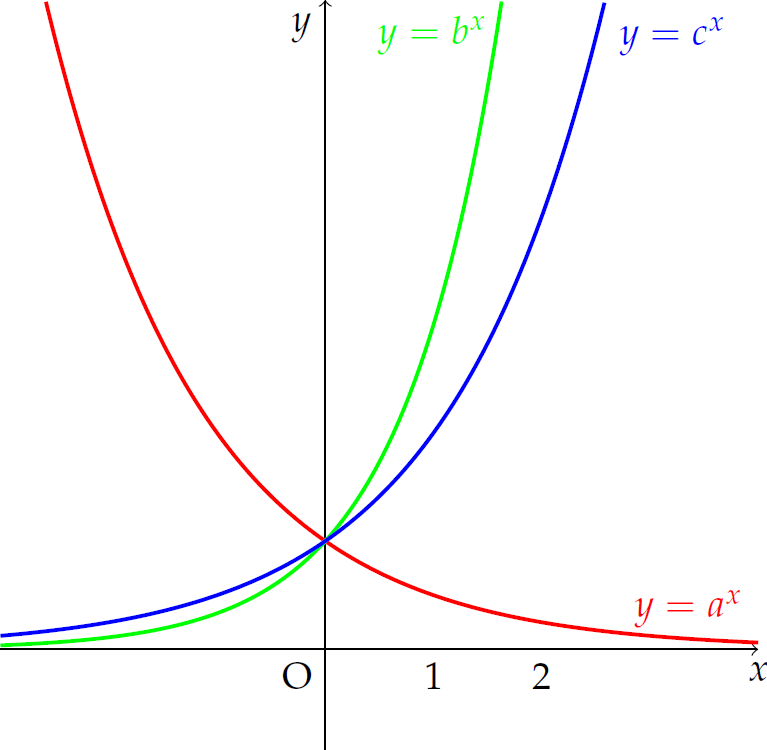
Mệnh đề nào dưới đây là đúng?
| \(a< b< c\) | |
| \(a< c< b\) | |
| \(b< c< a\) | |
| \(c< a< b\) |
Cho \(a,\,b,\,c\) dương và khác \(1\). Đồ thị hàm số \(y=\log_ax\), \(y=\log_bx\) và \(y=\log_cx\) được cho trong hình vẽ.
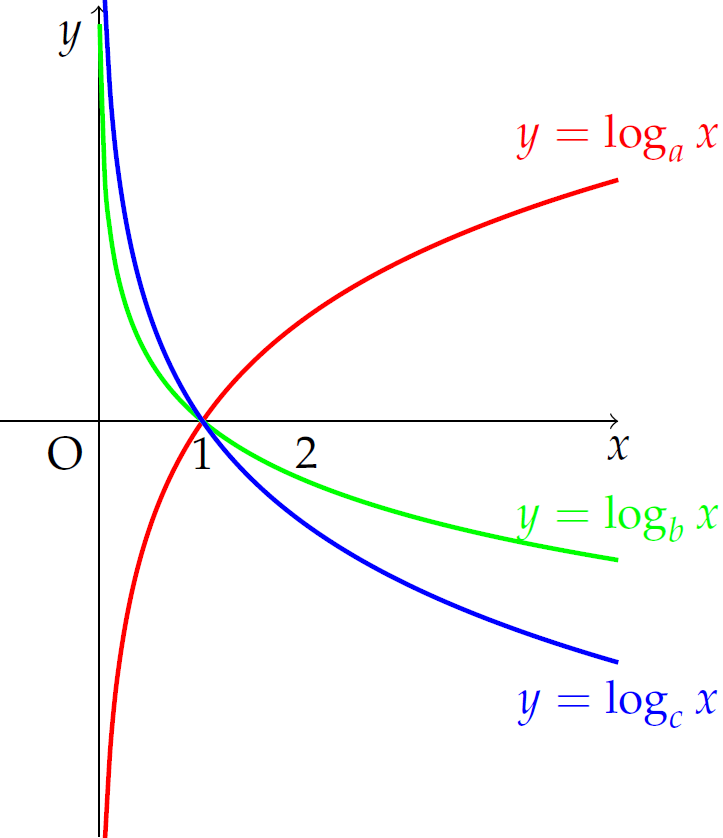
Khẳng định nào dưới đây là đúng?
| \(a>c>b\) | |
| \(b>c>a\) | |
| \(c>b>a\) | |
| \(a>b>c\) |
Gọi tam giác cong \(OAB\) là hình phẳng giới hạn bởi đồ thị các hàm số \(y=2x^2\), \(y=3-x\), \(y=0\) (như hình vẽ).
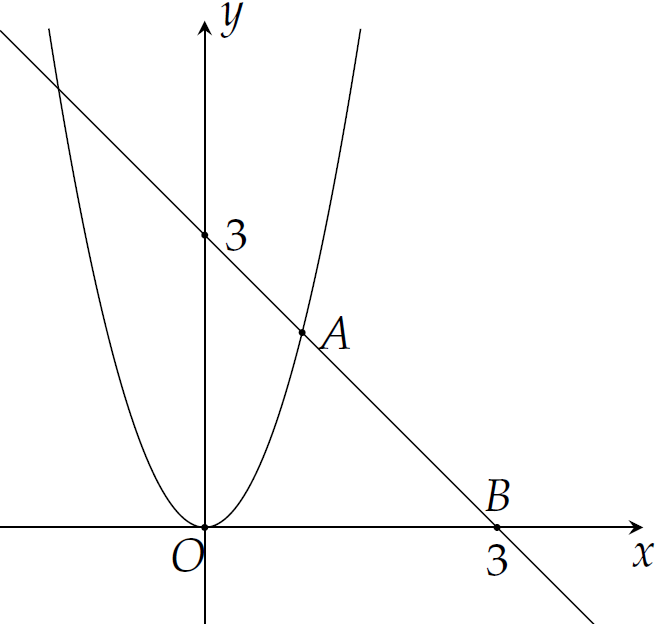
Tính diện tích \(S\) của tam giác cong \(OAB\).
| \(S=\dfrac{8}{3}\) | |
| \(S=\dfrac{4}{3}\) | |
| \(S=\dfrac{5}{3}\) | |
| \(S=\dfrac{10}{3}\) |
