Hãy liệt kê các phần tử của tập hợp $$X=\left\{x\in\mathbb{Q}\colon\left(x^2-x-6\right)\left(x^2-5\right)=0\right\}$$
| \(X=\left\{\sqrt{5};3\right\}\) | |
| \(X=\left\{-\sqrt{5};-2;\sqrt{5};3\right\}\) | |
| \(X=\left\{-2;3\right\}\) | |
| \(X=\left\{-\sqrt{5};\sqrt{5}\right\}\) |
Cho tập hợp \(X=\left\{x\in\mathbb{Z}\colon\left(x^2-9\right)\left(x^2-\left(1+\sqrt{2}\right)x+\sqrt{2}\right)=0\right\}\). Hỏi tập \(X\) có bao nhiêu phần tử?
| \(1\) | |
| \(2\) | |
| \(3\) | |
| \(4\) |
Cho tập hợp \(X=\left\{x\in\mathbb{N}\colon\left(x^2-4\right)(x-1)\left(2x^2-7x+3\right)=0\right\}\). Tính tổng \(S\) các phần tử của tập hợp \(X\).
| \(S=4\) | |
| \(S=\dfrac{9}{2}\) | |
| \(S=5\) | |
| \(S=6\) |
Cho hai tập hợp \(A=\left\{x\in\mathbb{R}\colon\left(2x-x^2\right)\left(2x^2-3x-2\right)=0\right\}\) và \(B=\left\{n\in\mathbb{N}^*\colon3< n^2<30\right\}\). Tìm \(A\cap B\).
| \(A\cap B=\{2;4\}\) | |
| \(A\cap B=\{2\}\) | |
| \(A\cap B=\{4;5\}\) | |
| \(A\cap B=\{3\}\) |
Hãy liệt kê các phần tử của tập hợp $$X=\left\{x\in\mathbb{R}\colon x^2+x+1=0\right\}$$
| \(X=0\) | |
| \(X=\{0\}\) | |
| \(X=\varnothing\) | |
| \(X=\{\varnothing\}\) |
Hãy viết tập hợp \(X=\left\{x\in\mathbb{R}\colon2x^2-5x+3=0\right\}\) dưới dạng liệt kê phần tử.
| \(X=\{0\}\) | |
| \(X=\{1\}\) | |
| \(X=\left\{\dfrac{3}{2}\right\}\) | |
| \(X=\left\{1;\dfrac{3}{2}\right\}\) |
Số phần tử của tập hợp $A=\left\{ {{k}^{2}}+1|k\in \mathbb{Z},\left| k \right|\le 2 \right\}$ là
| $1$ | |
| $2$ | |
| $3$ | |
| $5$ |
Cho hai tập hợp \(A=\left\{-\dfrac{1}{2};1;2\right\}\) và \(B=\left\{x\in\mathbb{Z}\colon2x^2-x-1=0\right\}\). Tìm tập hợp \(A\cap B\).
| \(\left\{-\dfrac{1}{2}\right\}\) | |
| \(\left\{-\dfrac{1}{2};1\right\}\) | |
| \(\{1\}\) | |
| \(\{1;2\}\) |
Cho hai tập hợp \(A=\{1;2;3\}\) và \(B=\{1;2;3;4;5\}\). Có tất cả bao nhiêu tập \(X\) sao cho \(A\subset X\subset B\)?
| \(4\) | |
| \(5\) | |
| \(6\) | |
| \(8\) |
Cho tập hợp \(M=\left\{(x;y)\colon x,\,y\in\mathbb{N}\text{ và }x+y=1\right\}\). Hỏi \(M\) có bao nhiêu phần tử?
| \(0\) | |
| \(1\) | |
| \(2\) | |
| \(4\) |
Tập hợp \(A=\left\{k^2+1\colon k\in\mathbb{Z},\,|k|\leq2\right\}\) có bao nhiêu phần tử?
| \(1\) | |
| \(2\) | |
| \(3\) | |
| \(5\) |
Cho tập hợp $$A=\left\{x\in\mathbb{N}\colon x\text{ là ước chung của }36\text{ và }120\right\}$$Hãy liệt kê các phần tử của tập hợp \(A\).
| \(A=\{1;2;3;4;6;12\}\) | |
| \(A=\{1;2;4;6;8;12\}\) | |
| \(A=\{2;4;6;8;10;12\}\) | |
| \(A=\{1;36;120\}\) |
Mệnh đề nào sau đây tương đương với mệnh đề \(A\neq\varnothing\)?
| \(\forall x,\,x\in A\) | |
| \(\exists x,\,x\in A\) | |
| \(\exists x,\,x\notin A\) | |
| \(\forall x,\,x\subset A\) |
Kí hiệu nào sau đây dùng để viết đúng mệnh đề "\(\sqrt{2}\) không phải là số vô tỉ"?
| \(\sqrt{2}\neq\mathbb{Q}\) | |
| \(\sqrt{2}\not\subset\mathbb{Q}\) | |
| \(\sqrt{2}\notin\mathbb{Q}\) | |
| \(\sqrt{2}\in\mathbb{Q}\) |
Kí hiệu nào sau đây dùng để viết đúng mệnh đề "\(7\) là số tự nhiên"?
| \(7\subset\mathbb{N}\) | |
| \(7\in\mathbb{N}\) | |
| \(7\notin\mathbb{N}\) | |
| \(7\leq\mathbb{N}\) |
Tìm tập xác định của hàm số $$y=\sqrt{x-1}-\dfrac{3x-1}{\left(x^2-4\right)\sqrt{5-x}}$$
| $[1;5]\setminus\{2\}$ | |
| $(-\infty;5]$ | |
| $[1;5)\setminus\{2\}$ | |
| $[1;+\infty)\setminus\{2;5\}$ |
Tìm tập xác định của hàm số $$y=\dfrac{\sqrt{x+1}}{\left(x^2-5x+6\right)\sqrt{4-x}}$$
| $[-1;4)\setminus\{2;3\}$ | |
| $[-1;4)$ | |
| $(-1;4]\setminus\{2;3\}$ | |
| $(-1;4)\setminus\{2;3\}$ |
Tìm các giá trị thực của tham số $m$ để phương trình $$\left(x-1\right)\left(x^2-4mx-4\right)=0$$có ba nghiệm phân biệt.
| $m\in\Bbb{R}$ | |
| $m\neq0$ | |
| $m\neq\dfrac{3}{4}$ | |
| $m\neq-\dfrac{3}{4}$ |
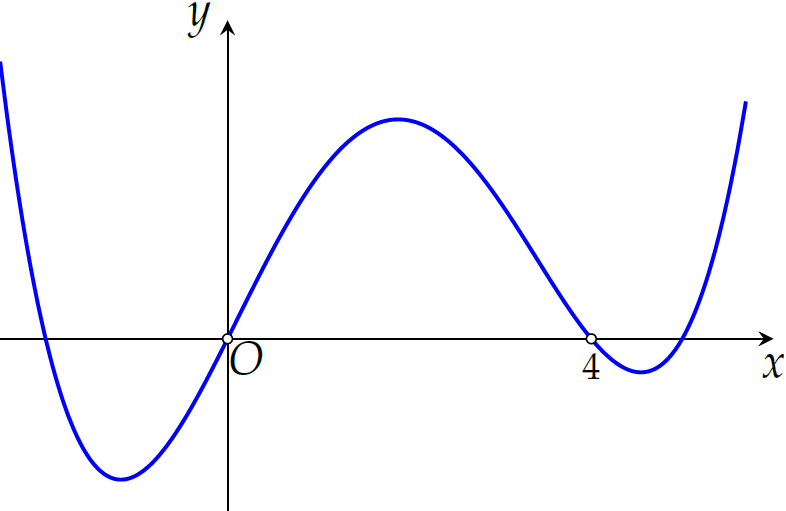
Cho hàm số bậc bốn \(y=f(x)\) có đồ thị như hình trên. Số điểm cực trị của hàm số \(g(x)=f\left(x^3+3x^2\right)\) là
| \(5\) | |
| \(3\) | |
| \(7\) | |
| \(11\) |
Cho tập hợp $A$ có $7$ phần tử. Số tập con gồm $3$ phần tử của tập hợp $A$ là
| $\mathrm{A}_7^3$ | |
| $3^7$ | |
| $\mathrm{C}_7^3$ | |
| $7^3$ |
