Mệnh đề nào sau đây sai?

	\(A\cap B=A\Leftrightarrow A\subset B\)
	\(A\cup B=A\Leftrightarrow B\subset A\)
	\(A\setminus B=A\Leftrightarrow A\cap B=\varnothing\)
	\(A\setminus B=\varnothing\Leftrightarrow A\cap B=\varnothing\)

Cho hai tập hợp \(M,\,N\) sao cho \(M\subset N\). Mệnh đề nào sau đây đúng?

	\(M\cap N=N\)
	\(M\setminus N=N\)
	\(M\cap N=M\)
	\(M\setminus N=M\)

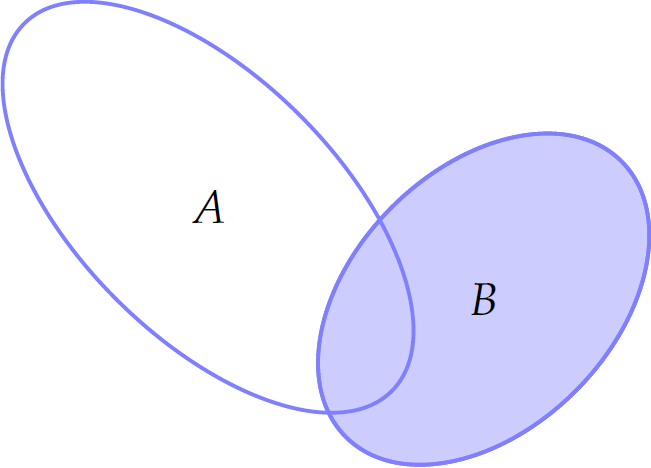
Cho \(A,\,B\) là hai tập hợp được minh họa như hình vẽ. Phần không tô màu trong hình là tập hợp nào sau đây?

	\(A\cap B\)
	\(A\cup B\)
	\(A\setminus B\)
	\(B\setminus A\)

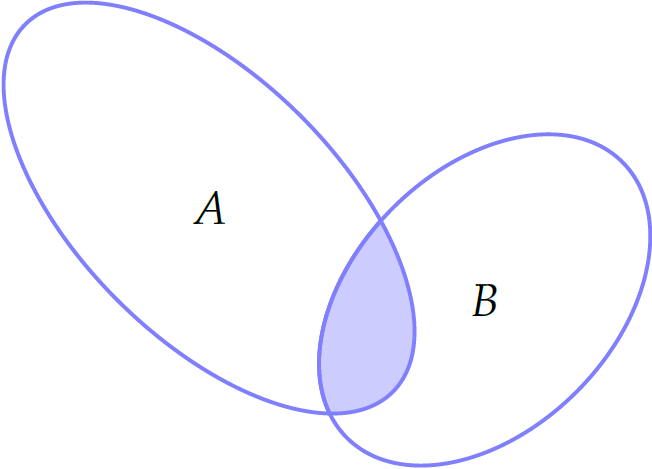
Cho \(A,\,B\) là hai tập hợp được minh họa như hình vẽ. Phần tô màu trong hình là tập hợp nào sau đây?

	\(A\cap B\)
	\(A\cup B\)
	\(A\setminus B\)
	\(B\setminus A\)

Cho các tập hợp

• \(M=\{x\in\mathbb{N}^*\colon x\text{ là bội của }2\}\),
• \(N=\{x\in\mathbb{N}^*\colon x\text{ là bội của }6\}\),
• \(P=\{x\in\mathbb{N}\colon x\text{ là ước của }2\}\),
• \(Q=\{x\in\mathbb{N}\colon x\text{ là ước của }6\}\).

Mệnh đề nào sau đây đúng?

	\(M\subset N\)
	\(Q\subset P\)
	\(M\cap N=N\)
	\(P\cap Q=Q\)

Cho tập hợp \(A\neq\varnothing\). Mệnh đề nào sau đây sai?

	\(A\cap\varnothing=A\)
	\(A\cap\varnothing=\varnothing\)
	\(\varnothing\cap\varnothing=\varnothing\)
	\(A\cap A=A\)

Cho tập hợp \(A\neq\varnothing\). Mệnh đề nào sau đây sai?

	\(A\cup\varnothing=\varnothing\)
	\(\varnothing\cup A=A\)
	\(\varnothing\cup\varnothing=\varnothing\)
	\(A\cup A=A\)

Cho tập hợp \(A\neq\varnothing\). Mệnh đề nào sau đây đúng?

	\(A\setminus\varnothing=\varnothing\)
	\(\varnothing\setminus A=A\)
	\(\varnothing\setminus\varnothing=A\)
	\(A\setminus A=\varnothing\)

Cho \(x\) là một phần tử của tập hợp \(A\). Xét các mệnh đề sau:

1. \(x\in A\)
2. \(\{x\}\in A\)
3. \(x\subset A\)
4. \(\{x\}\subset A\)

Trong các mệnh đề trên, mệnh đề nào đúng?

	I và II
	I và III
	I và IV
	II và IV

Cho \(A\) là một tập hợp. Trong các mệnh đề sau, mệnh đề nào đúng?

	\(A\in A\)
	\(\varnothing\in A\)
	\(A\subset A\)
	\(A\in\{A\}\)

Hình nào sau đây minh họa tập \(A\) là tập con của tập \(B\)?

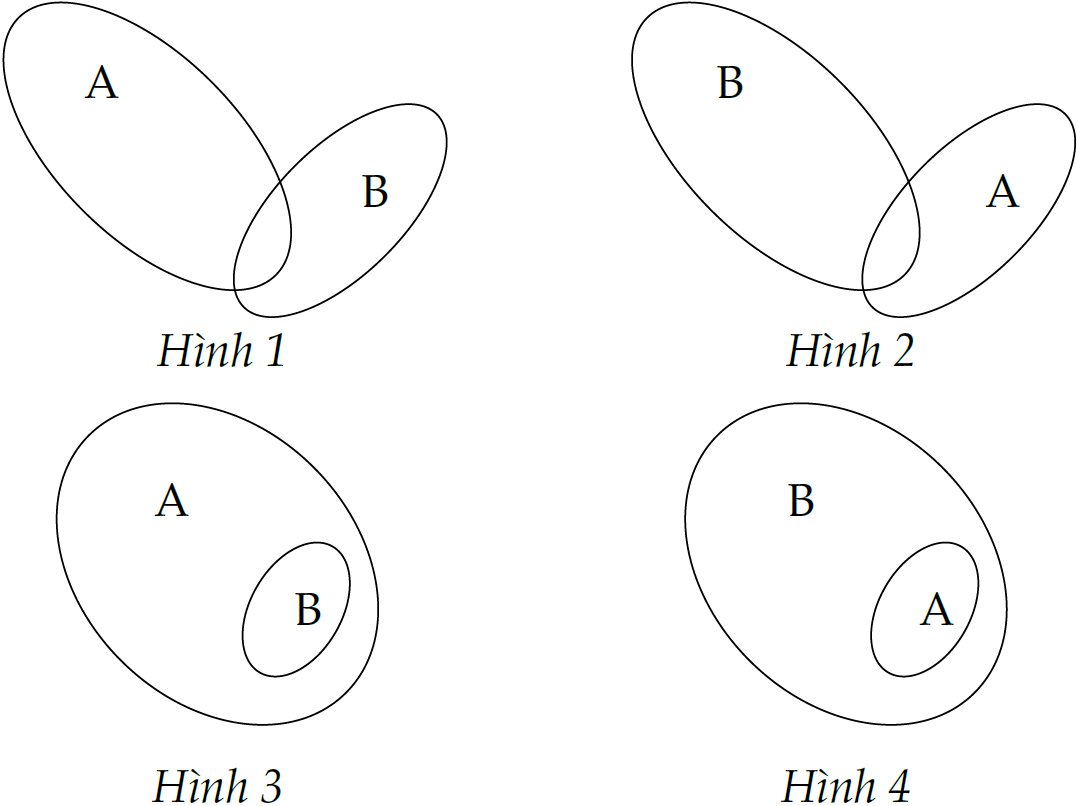
	Hình 1
	Hình 2
	Hình 3
	Hình 4

Kí hiệu nào sau đây dùng để viết đúng mệnh đề "\(7\) là số tự nhiên"?

	\(7\subset\mathbb{N}\)
	\(7\in\mathbb{N}\)
	\(7\notin\mathbb{N}\)
	\(7\leq\mathbb{N}\)

Cho tập hợp $A$ có $7$ phần tử. Số tập con gồm $3$ phần tử của tập hợp $A$ là

	$\mathrm{A}_7^3$
	$3^7$
	$\mathrm{C}_7^3$
	$7^3$

Cho tập hợp $A$ có $15$ phần tử. Số tập con gồm hai phần tử của $A$ bằng

	$225$
	$30$
	$210$
	$105$

Một lớp học có $16$ học sinh học giỏi môn Toán; $12$ học sinh học giỏi môn Văn; $8$ học sinh vừa học giỏi môn Toán và Văn; $19$ học sinh không học giỏi cả hai môn Toán và Văn. Hỏi lớp học có bao nhiêu học sinh?

	$31$
	$39$
	$47$
	$54$

Lớp \(10A4\) có \(7\) học sinh giỏi Toán, \(5\) học sinh giỏi Lý, \(6\) học sinh giỏi Hóa, \(3\) học sinh giỏi cả Toán và Lý, \(4\) học sinh giỏi cả Toán và Hóa, \(2\) học sinh giỏi cả Lý và Hóa, \(1\) học sinh giỏi cả Toán, Lý, Hóa. Tìm số học sinh giỏi ít nhất một môn (Toán, Lý, Hóa) của lớp 10A4.

	\(9\)
	\(10\)
	\(18\)
	\(28\)

Lớp \(10A4\) có \(7\) học sinh giỏi Toán, \(5\) học sinh giỏi Lý, \(6\) học sinh giỏi Hóa, \(3\) học sinh giỏi cả Toán và Lý, \(4\) học sinh giỏi cả Toán và Hóa, \(2\) học sinh giỏi cả Lý và Hóa, \(1\) học sinh giỏi cả Toán, Lý, Hóa. Tìm số học sinh giỏi đúng hai môn (Toán, Lý, Hóa) của lớp 10A4.

	\(6\)
	\(7\)
	\(9\)
	\(10\)

Một lớp học có \(50\) học sinh, trong đó có \(30\) em biết chơi bóng chuyền, \(25\) em biết chơi bóng đá, \(10\) em biết chơi cả bóng đá và bóng chuyền. Hỏi có bao nhiêu em không biết chơi cả bóng đá và bóng chuyền?

	\(15\)
	\(5\)
	\(20\)
	\(45\)

Lớp 10A4 có \(45\) học sinh, trong đó có \(17\) bạn giỏi Văn, \(25\) bạn giỏi Toán và \(13\) bạn không giỏi cả Văn và Toán. Hỏi lớp 10A4 có bao nhiêu bạn giỏi cả Văn và Toán?

	\(42\)
	\(32\)
	\(17\)
	\(10\)

Cho hai tập hợp \(A=\{0;2\}\) và \(B=\{0;1;2;3;4\}\). Có bao nhiêu tập hợp \(X\) thỏa mãn \(A\cup X=B\)?

	\(2\)
	\(3\)
	\(4\)
	\(5\)