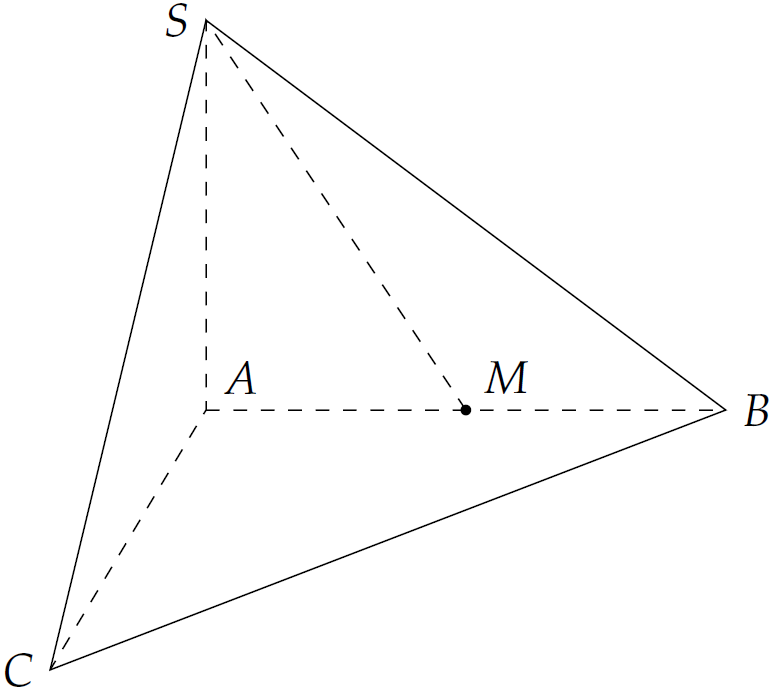
Cho hình chóp \(S.ABC\) có đáy là tam giác vuông tại \(A\), \(AB=2a\), \(AC=4a\), \(SA\) vuông góc với mặt phẳng đáy và \(SA=a\) (minh họa như hình vẽ). Gọi \(M\) là trung điểm của \(AB\). Khoảng cách giữa hai đường thẳng \(SM\) và \(BC\) bằng
| \(\dfrac{2a}{3}\) | |
| \(\dfrac{a\sqrt{6}}{3}\) | |
| \(\dfrac{a\sqrt{3}}{3}\) | |
| \(\dfrac{a}{2}\) |
Cho tứ diện $OABC$ có $OA,\,OB,\,OC$ đôi một vuông góc với nhau và $OA=OB=OC=a$. Gọi $D$ là trung điểm của đoạn $BC$. Khoảng cách giữa hai đường thẳng $OD$ và $AB$ bằng
| $\dfrac{a\sqrt{3}}{3}$ | |
| $\dfrac{a\sqrt{6}}{2}$ | |
| $\dfrac{a\sqrt{6}}{3}$ | |
| $\dfrac{a\sqrt{3}}{2}$ |
Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác vuông tại $A$, $\widehat{ABC}=30^\circ$. Tam giác $SBC$ là tam giác đều cạnh $a$ và nằm trong mặt phẳng vuông góc với đáy. Thể tích khối chóp $S.ABC$ là
| $\dfrac{3a^3}{16}$ | |
| $\dfrac{a^3}{16}$ | |
| $\dfrac{a^3\sqrt{3}}{16}$ | |
| $\dfrac{3\sqrt{3}a^3}{16}$ |
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình chữ nhật và $AD=a$, $AB=2a$. Biết tam giác $SAB$ là tam giác đều và mặt phẳng $(SAB)$ vuông góc với mặt phẳng $(ABCD)$. Tính khoảng cách từ điểm $A$ đến mặt phẳng $(SBD)$.
| $\dfrac{a\sqrt{3}}{4}$ | |
| $\dfrac{a\sqrt{3}}{2}$ | |
| $a\sqrt{3}$ | |
| $\dfrac{a\sqrt{3}}{3}$ |
Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác vuông tại $A$, $AB=a$, $AC=2a$, $SA$ vuông góc với mặt phẳng đáy và $SB$ tạo với mặt đáy một góc $60^\circ$. Gọi $M,\,N$ lần lượt là trung điểm của $SB$ và $BC$. Thể tích khối chóp $A.SCNM$ bằng
| $\dfrac{\sqrt{3}}{4}a^3$ | |
| $\dfrac{\sqrt{3}}{2}a^3$ | |
| $\dfrac{3\sqrt{3}}{4}a^3$ | |
| $\dfrac{3\sqrt{3}}{2}a^3$ |
Cho hình chóp đều $S.ABCD$ có chiều cao $a$, $AC=2a$ (tham khảo hình bên).
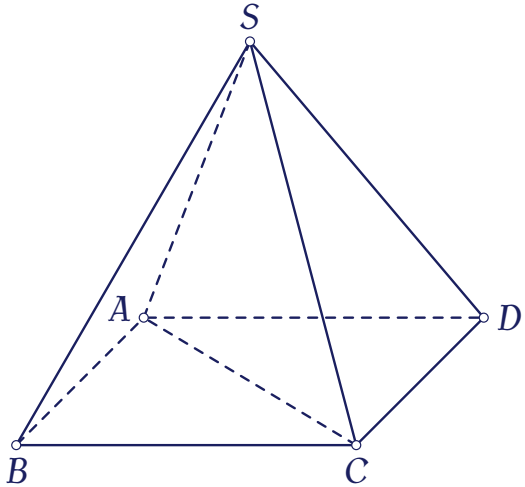
Khoảng cách từ $B$ đến mặt phẳng $(SCD)$ bằng
| $\dfrac{\sqrt{3}}{3}a$ | |
| $\sqrt{2}a$ | |
| $\dfrac{2\sqrt{3}}{3}a$ | |
| $\dfrac{\sqrt{2}}{2}a$ |
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình chữ nhật và $AD=a$, $AB=2a$. Biết tam giác $SAB$ là tam giác đều và mặt phẳng $(SAB)$ vuông góc với mặt phẳng $(ABCD)$. Tính khoảng cách từ điểm $A$ đến mặt phẳng $(SBD)$.
| $\dfrac{a\sqrt{3}}{4}$ | |
| $\dfrac{a\sqrt{3}}{2}$ | |
| $a\sqrt{3}$ | |
| $\dfrac{a\sqrt{3}}{3}$ |
Cho khối chóp tứ giác $S.ABCD$ có thể tích $V$ và đáy là hình bình hành. Gọi $N$ là điểm trên cạnh $SD$ sao cho $ND=2NS$. Một mặt phẳng chứa $BN$ và song song với $AC$, cắt $SA,\,SC$ lần lượt tại $P,\,Q$. Gọi $V'$ là thể tích của khối chóp $S.BPNQ$. Khẳng định nào dưới đây đúng?
| $\dfrac{V'}{V}=\dfrac{1}{6}$ | |
| $\dfrac{V'}{V}=\dfrac{2}{5}$ | |
| $\dfrac{V'}{V}=\dfrac{1}{3}$ | |
| $\dfrac{V'}{V}=\dfrac{1}{4}$ |
Cho hình chóp tứ giác $S.ABCD$. Gọi $M$ và $N$ lần lượt là trung điểm của $SA$ và $SC$. Khẳng định nào sau đây đúng?
| $MN\parallel(ABCD)$ | |
| $MN\parallel(SAB)$ | |
| $MN\parallel(SCD)$ | |
| $MN\parallel(SBC)$ |
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình bình hành. Gọi $I$ là trung điểm $SA$. Thiết diện của hình chóp $S.ABCD$ cắt bởi $(IBC)$ là
| Tam giác $IBC$ | |
| Hình thang $IGBC$ ($G$ là trung điểm $SB$) | |
| Hình thang $IJCB$ ($J$ là trung điểm $SD$) | |
| Tứ giác $IBCD$ |
Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác vuông tại $A$ và có $AB=a$, $BC=a\sqrt{3}$. Mặt bên $(SAB)$ là tam giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng $(ABC)$. Tính theo $a$ thể tích $V$ của khối chóp $S.ABC$.
| $V=\dfrac{a^3\sqrt{6}}{12}$ | |
| $V=\dfrac{a^3\sqrt{6}}{4}$ | |
| $V=\dfrac{a^3\sqrt{6}}{6}$ | |
| $V=\dfrac{a^3\sqrt{6}}{3}$ |
Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác đều cạnh $a$, cạnh bên $SA$ vuông góc với mặt phẳng đáy, góc giữa $SA$ và mặt phẳng $(SBC)$ bằng $45^\circ$ (tham khảo hình bên).
Thể tích của khối chóp $S.ABC$ bằng
| $\dfrac{a^3}{8}$ | |
| $\dfrac{3a^3}{8}$ | |
| $\dfrac{\sqrt{3}a^3}{12}$ | |
| $\dfrac{a^3}{4}$ |
Cho tứ diện $OABC$ có $OA$, $OB$, $OC$ đôi một vuông góc. Gọi $OH$ là đường cao của tứ diện. Khi đó $H$ là
| Trọng tâm $\triangle ABC$ | |
| Trực tâm $\triangle ABC$ | |
| Tâm đường tròn nội tiếp $\triangle ABC$ | |
| Tâm đường tròn ngoại tiếp $\triangle ABC$ |
Cho tứ diện $ABCD$ có hai mặt $\left(ABC\right)$ và $\left(BCD\right)$ vuông góc với nhau. Biết rằng $\triangle ABC$ đều cạnh $2a$ và $M$ là trung điểm $BC$. Tính khoảng cách từ điểm $A$ đến mặt phẳng $\left(BCD\right)$.
| $2a$ | |
| $a\sqrt{3}$ | |
| $2a\sqrt{3}$ | |
| $\dfrac{a\sqrt{3}}{2}$ |
Cho hình chóp $S.ABC$ có đáy là tam giác $ABC$ vuông tại $B$, cạnh bên $SA$ vuông góc với đáy. Gọi $H$ là chân đường cao kẻ từ $A$ của tam giác $SAB$. Khẳng định nào dưới đây sai?
| $SA\bot BC$ | |
| $AH\bot BC$ | |
| $AH\bot AC$ | |
| $AH\bot SC$ |
Cho hình chóp $S.ABC$ có đáy là tam giác $ABC$ vuông tại $B$, cạnh bên $SA$ vuông góc với đáy. Gọi $H$ là chân đường cao kẻ từ $A$ của tam giác $SAB$. Khẳng định nào dưới đây sai?
| $SA\bot\left(ABC\right)$ | |
| $AH\bot\left(ABC\right)$ | |
| $AH\bot\left(SBC\right)$ | |
| $BC\bot\left(SAB\right)$ |
Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác vuông tại \(B\). Biết \(AC=a\), \(BC=\dfrac{a}{2}\), \(SA=\dfrac{a\sqrt{3}}{2}\) và cạnh \(SA\) vuông góc với mặt phẳng đáy. Khoảng cách từ \(A\) đến mặt phẳng \((SBC)\) bằng
| \(\dfrac{a\sqrt{6}}{4}\) | |
| \(a\sqrt{6}\) | |
| \(\dfrac{a\sqrt{3}}{2}\) | |
| \(\dfrac{a\sqrt{6}}{2}\) |
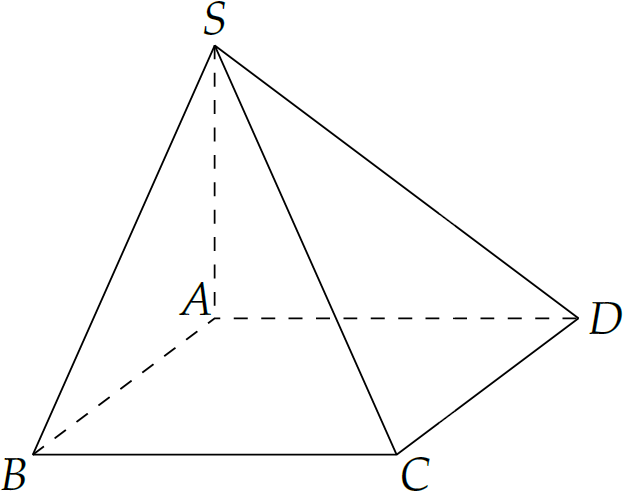
Cho hình chóp \(S.ABCD\) có đáy là hình vuông cạnh \(a\sqrt{3}\), \(SA\) vuông góc với mặt phẳng đáy và \(SA=a\sqrt{2}\) (như hình minh họa trên). Góc giữa đường thẳng \(SC\) và mặt phẳng \((ABCD)\) bằng
| \(45^\circ\) | |
| \(30^\circ\) | |
| \(60^\circ\) | |
| \(90^\circ\) |
Cho hình hộp chữ nhật $ABCD.A'B'C'D'$ có $AB=a$, $BC=2a$ và $AA'=3a$ (tham khảo hình bên).
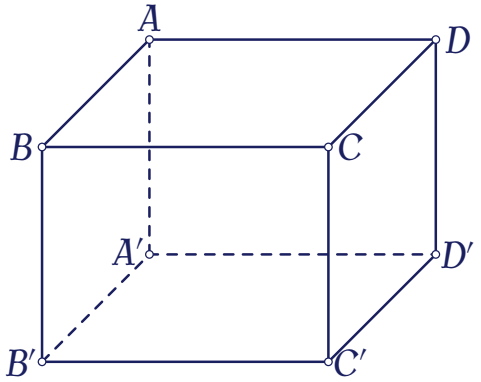
Khoảng cách giữa hai đường thẳng $BD$ và $A'C'$ bằng
| $a$ | |
| $a\sqrt{2}$ | |
| $2a$ | |
| $3a$ |
Khoảng cách giữa hai đường thẳng \(\Delta_1\colon\begin{cases}x=2+4t\\ y=-1+3t\end{cases}\) và \(\Delta_2\colon-3x+4y+5=0\) bằng
| \(-1\) | |
| \(1\) | |
| \(-\sqrt{5}\) | |
| \(\sqrt{5}\) |
