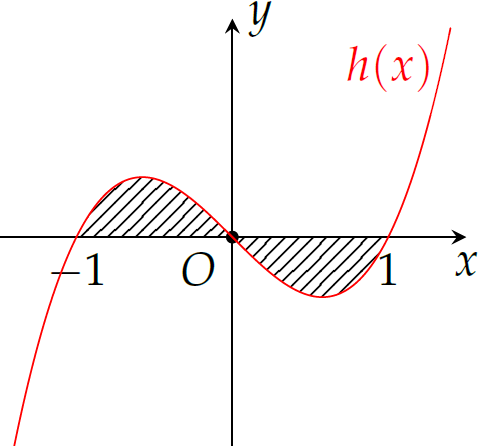
Cho đồ thị hàm số \(y=h(x)\). Diện tích hình phẳng (phần gạch chéo trong hình vẽ) bằng
| \(\displaystyle\int\limits_{-1}^{0}h(x)\mathrm{\,d}x+\displaystyle\int\limits_{0}^{1}h(x)\mathrm{\,d}x\) | |
| \(\displaystyle\int\limits_{-1}^{1}h(x)\mathrm{\,d}x\) | |
| \(\displaystyle\int\limits_{-1}^{0}h(x)\mathrm{\,d}x+\displaystyle\int\limits_{1}^{0}h(x)\mathrm{\,d}x\) | |
| \(-\displaystyle\int\limits_{-1}^{0}h(x)\mathrm{\,d}x+\displaystyle\int\limits_{0}^{1}h(x)\mathrm{\,d}x\) |
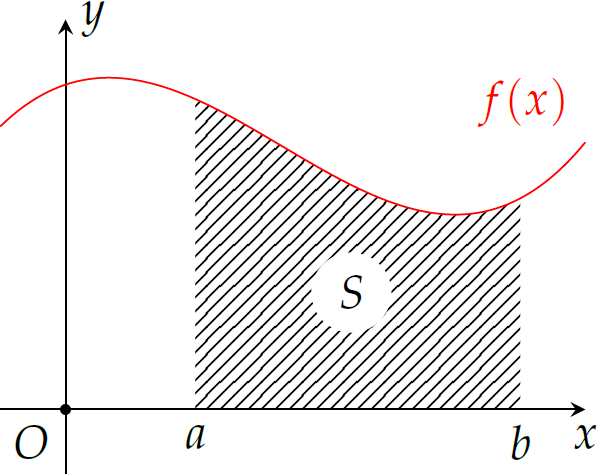
Diện tích hình phẳng \(S\) đối với hình vẽ trên là
| \(S=-\displaystyle\int\limits_{a}^{b}f(x)\mathrm{\,d}x\) | |
| \(S=\displaystyle\int\limits_{a}^{b}f(x)\mathrm{\,d}x\) | |
| \(S=\displaystyle\int\limits_{b}^{a}f(x)\mathrm{\,d}x\) | |
| \(S=\displaystyle\int\limits_{a}^{b}-f(x)\mathrm{\,d}x\) |
Gọi \(S\) là diện tích hình phẳng giới hạn bởi các đường \(y=f(x)\), trục hoành và hai đường thẳng \(x=-1\), \(x=2\) (như hình vẽ).
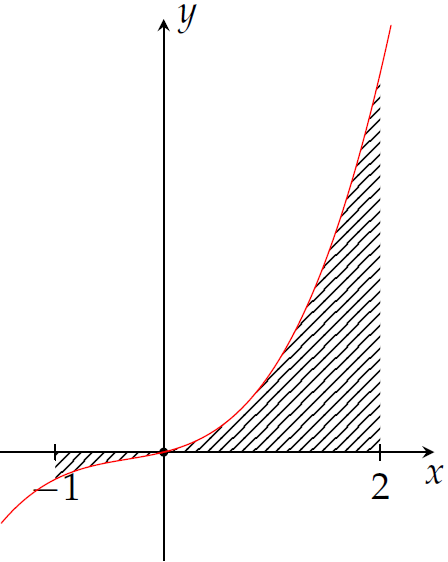
Đặt \(a=\displaystyle\int\limits_{-1}^{0}f(x)\mathrm{\,d}x\), \(b=\displaystyle\int\limits_{0}^{2}f(x)\mathrm{\,d}x\), mệnh đề nào dưới đây đúng?
| \(S=b-a\) | |
| \(S=b+a\) | |
| \(S=a-b\) | |
| \(S=-a-b\) |
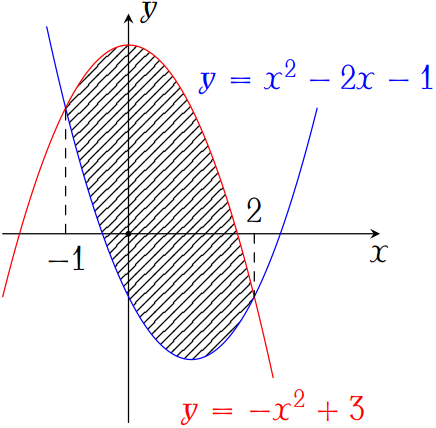
Diện tích phần hình phẳng gạch chéo trong hình vẽ trên được tính theo công thức nào dưới đây?
| \(\displaystyle\int\limits_{-1}^{2}(-2x+2)\mathrm{\,d}x\) | |
| \(\displaystyle\int\limits_{-1}^{2}(2x-2)\mathrm{\,d}x\) | |
| \(\displaystyle\int\limits_{-1}^{2}\left(-2x^2+2x+4\right)\mathrm{\,d}x\) | |
| \(\displaystyle\int\limits_{-1}^{2}\left(2x^2-2x-4\right)\mathrm{\,d}x\) |
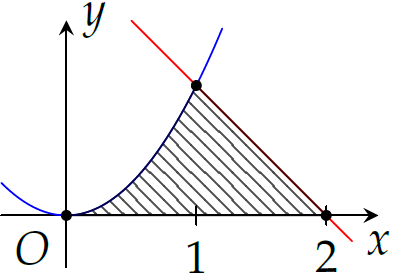
Tính diện tích hình phẳng tạo thành bởi parabol \(y=x^2\), đường thẳng \(y=-x+2\) và trục hoành trên đoạn \([0;2]\) (phần gạch sọc trong hình vẽ).
| \(\dfrac{5}{6}\) | |
| \(\dfrac{7}{6}\) | |
| \(\dfrac{2}{3}\) | |
| \(\dfrac{3}{5}\) |
Nếu hàm số \(y=f(x)\) liên tục trên đoạn \([a;b]\) thì diện tích \(S\) của hình phẳng giới hạn bởi đồ thị hàm số \(y=f(x)\), trục hoành và hai đường thẳng \(x=a\), \(x=b\) là
| \(\displaystyle\int\limits_{a}^{b}\left|f(x)-g(x)\right|\mathrm{\,d}x\) | |
| \(\displaystyle\int\limits_{b}^{a}\left|f(x)\right|\mathrm{\,d}x\) | |
| \(\displaystyle\int\limits_{a}^{b}f(x)\mathrm{\,d}x\) | |
| \(\displaystyle\int\limits_{a}^{b}\left|f(x)\right|\mathrm{\,d}x\) |
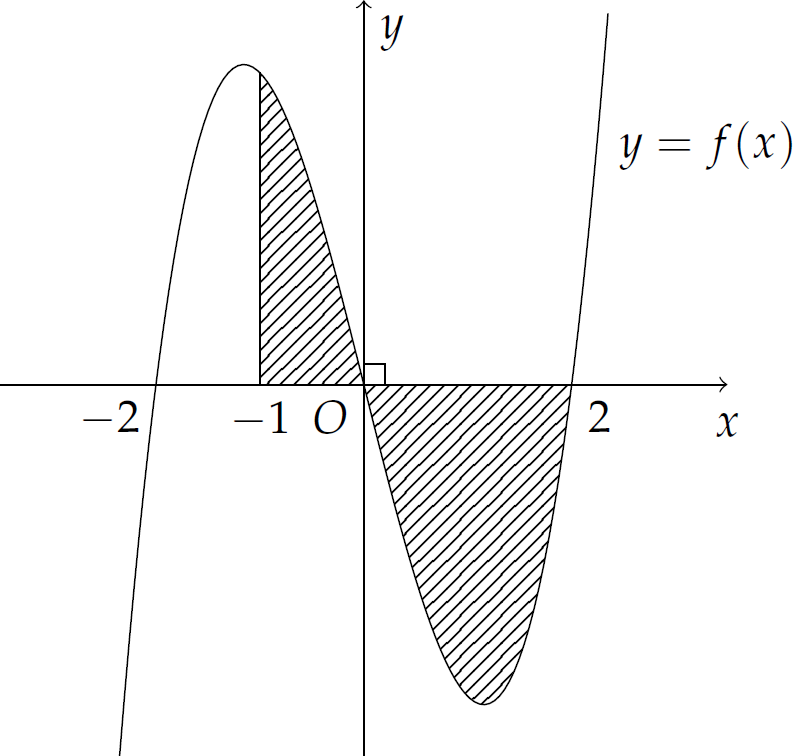
Cho hình phẳng \(H\) giới hạn bởi đồ thị hàm số \(y=f(x)\) trục \(Ox\) và đường thẳng \(x=-1\) (phần gạch sọc như hình trên). Gọi \(S\) là diện tích của hình phẳng \(H\). Mệnh đề nào dưới đây đúng?
| \(S=\displaystyle\int\limits_{-1}^0|f(x)|\mathrm{\,d}x-\displaystyle\int\limits_0^2|f(x)|\mathrm{\,d}x\) | |
| \(S=\displaystyle\int\limits_{-1}^2f(x)\mathrm{\,d}x\) | |
| \(S=\displaystyle\int\limits_{-1}^0f(x)\mathrm{\,d}x-\displaystyle\int\limits_0^2f(x)\mathrm{\,d}x\) | |
| \(S=\displaystyle\int\limits_{-1}^0f(x)\mathrm{\,d}x+\displaystyle\int\limits_0^2f(x)\mathrm{\,d}x\) |
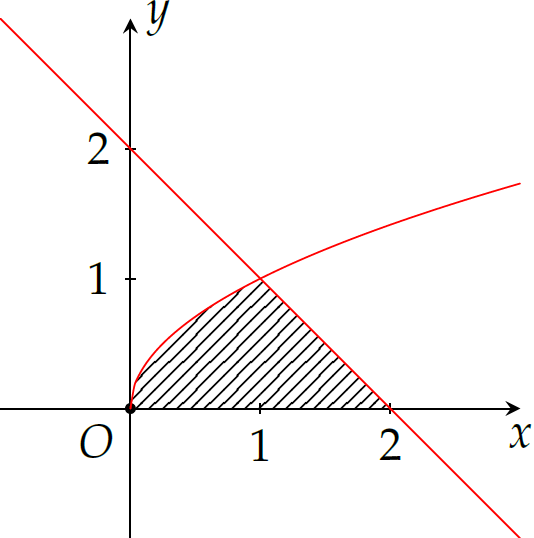
Cho \((H)\) là hình phẳng giới hạn bởi đồ thị của các hàm số \(y=\sqrt{x}\), \(y=0\), \(y=2-x\). Diện tích của \((H)\) là
| \(\dfrac{4\sqrt{2}-1}{3}\) | |
| \(\dfrac{8\sqrt{2}+3}{6}\) | |
| \(\dfrac{7}{6}\) | |
| \(\dfrac{5}{6}\) |
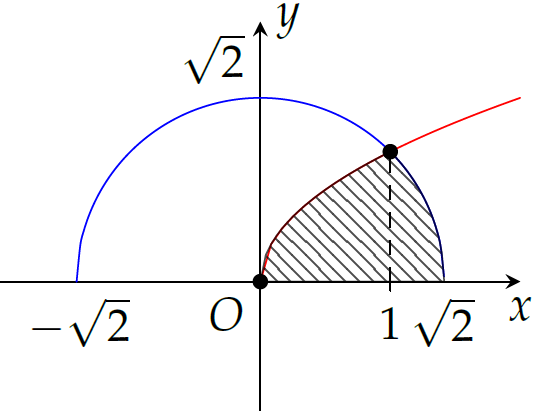
Cho \((H)\) là hình phẳng giới hạn bởi đường cong có phương trình \(y=\sqrt{x}\), nửa đường tròn có phương trình \(y=\sqrt{2-x^2}\) (với \(0\leq x\leq\sqrt{2}\)) và trục hoành (phần tô đậm trong hình vẽ). Diện tích của \((H)\) bằng
| \(\dfrac{3\pi+2}{12}\) | |
| \(\dfrac{4\pi+2}{12}\) | |
| \(\dfrac{3\pi+1}{12}\) | |
| \(\dfrac{4\pi+1}{6}\) |
Cho hàm số \(f(x)\) liên tục trên đoạn \([a;b]\). Diện tích hình phẳng giới hạn bởi đường cong \(y=f(x)\), trục hoành, các đường thẳng \(x=a\), \(x=b\) là
| \(\displaystyle\int\limits_{b}^{a}f(x)\mathrm{\,d}x\) | |
| \(\displaystyle\int\limits_{a}^{b}f(x)\mathrm{\,d}x\) | |
| \(\displaystyle\int\limits_{a}^{b}\left|f(x)\right|\mathrm{\,d}x\) | |
| \(-\displaystyle\int\limits_{a}^{b}f(x)\mathrm{\,d}x\) |
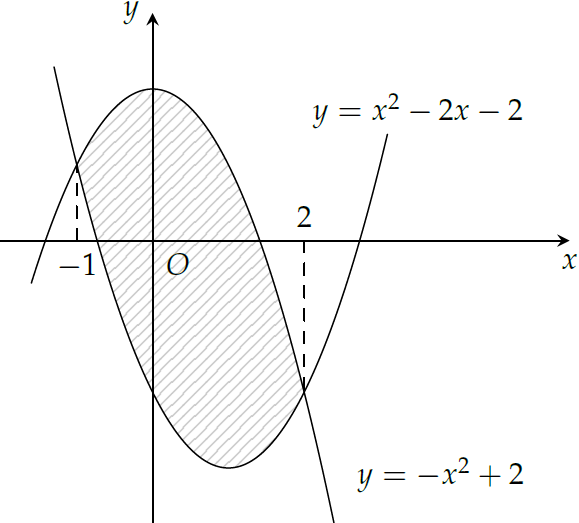
Diện tích phần hình phẳng được gạch chéo trong hình bên bằng
| \(\displaystyle\int\limits_{-1}^{2}{\left(-2x^2+2x+4\right)\mathrm{\,d}x}\) | |
| \(\displaystyle\int\limits_{-1}^{2}{\left(2x^2-2x-4\right)\mathrm{\,d}x}\) | |
| \(\displaystyle\int\limits_{-1}^{2}{\left(-2x^2-2x+4\right)\mathrm{\,d}x}\) | |
| \(\displaystyle\int\limits_{-1}^{2}{\left(2x^2+2x-4\right)\mathrm{\,d}x}\) |
Gọi \(S\) là diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y=f(x)\), trục hoành, \(x=a\), \(x=b\).
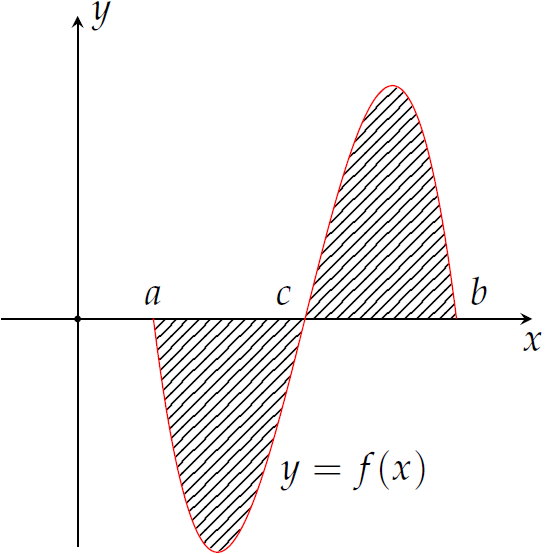
Khi đó \(S\) được tính theo công thức nào dưới đây?
| \(S=\displaystyle\int\limits_{a}^{b}f(x)\mathrm{\,d}x\) | |
| \(S=\displaystyle\int\limits_{a}^{c}f(x)\mathrm{\,d}x+\displaystyle\int\limits_{c}^{b}f(x)\mathrm{\,d}x\) | |
| \(S=-\displaystyle\int\limits_{a}^{c}f(x)\mathrm{\,d}x+\displaystyle\int\limits_{c}^{b}f(x)\mathrm{\,d}x\) | |
| \(S=\left|\displaystyle\int\limits_{a}^{c}f(x)\mathrm{\,d}x+\displaystyle\int\limits_{c}^{b}f(x)\mathrm{\,d}x\right|\) |
Cho hàm số \(y=f(x)\) liên tục trên \([a;b]\). Diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y=f(x)\), trục hoành và hai đường thẳng \(x=a\), \(x=b\) được xác định bởi công thức
| \(S=\displaystyle\int\limits_{a}^{b}f(x)\mathrm{\,d}x\) | |
| \(S=\displaystyle\int\limits_{b}^{a}\left|f(x)\right|\mathrm{\,d}x\) | |
| \(S=\displaystyle\int\limits_{a}^{b}\left|f(x)\right|\mathrm{\,d}x\) | |
| \(S=-\displaystyle\int\limits_{b}^{a}f(x)\mathrm{\,d}x\) |
Cho hàm số \(y=f(x)\) liên tục trên \([a;b]\). Gọi \(D\) là hình phẳng giới hạn bởi đồ thị hàm số \(y=f(x)\), trục hoành và hai đường thẳng \(x=a\), \(x=b\) (\(a<b\)). Diện tích hình phẳng \(D\) được xác định bởi công thức
| \(S=\displaystyle\int\limits_{a}^{b}f(x)\mathrm{\,d}x\) | |
| \(S=\displaystyle\int\limits_{a}^{b}\left|f(x)\right|\mathrm{\,d}x\) | |
| \(S=\pi\displaystyle\int\limits_{a}^{b}f^2(x)\mathrm{\,d}x\) | |
| \(S=\displaystyle\int\limits_{a}^{b}f^2(x)\mathrm{\,d}x\) |
Gọi tam giác cong \(OAB\) là hình phẳng giới hạn bởi đồ thị các hàm số \(y=2x^2\), \(y=3-x\), \(y=0\) (như hình vẽ).
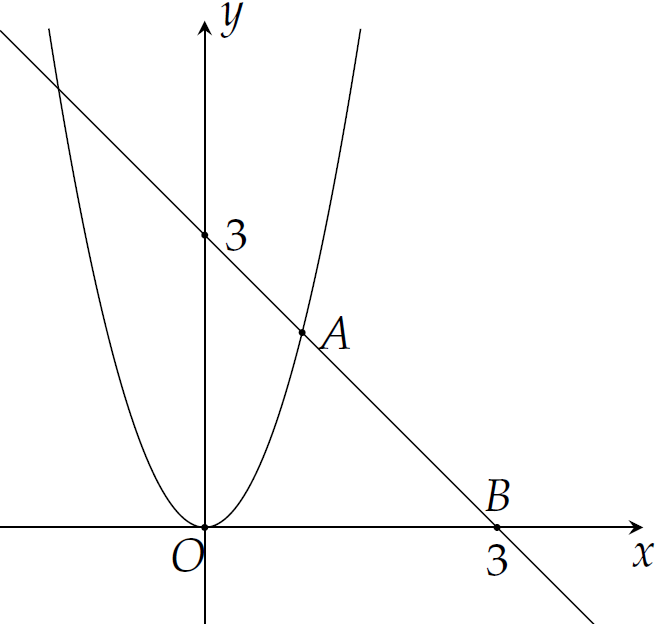
Tính diện tích \(S\) của tam giác cong \(OAB\).
| \(S=\dfrac{8}{3}\) | |
| \(S=\dfrac{4}{3}\) | |
| \(S=\dfrac{5}{3}\) | |
| \(S=\dfrac{10}{3}\) |
Tính diện tích hình phẳng giới hạn bởi các đường \(y=x^2\), \(y=-\dfrac{1}{3}x+\dfrac{4}{3}\) và trục hoành như hình vẽ.
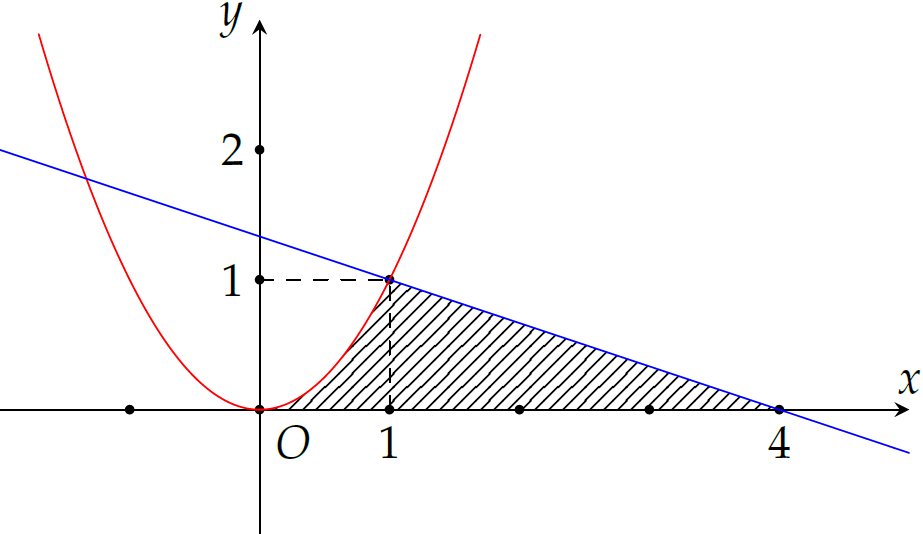
| \(\dfrac{7}{3}\) | |
| \(\dfrac{56}{3}\) | |
| \(\dfrac{39}{2}\) | |
| \(\dfrac{11}{6}\) |
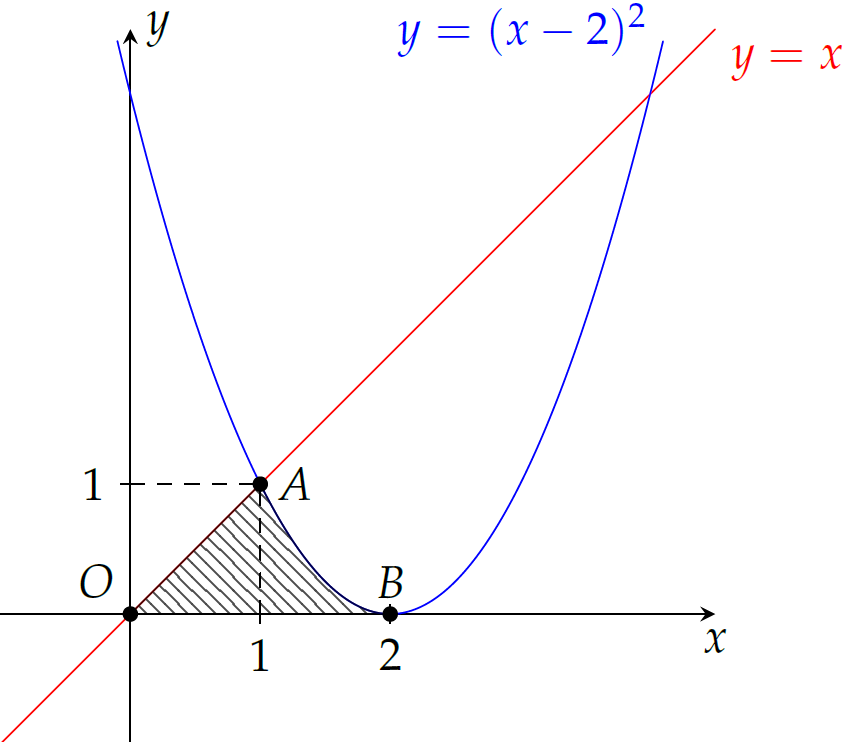
Tính diện tích phần hình phẳng gạch chéo (tam giác cong \(OAB\)) trong hình vẽ.
| \(\dfrac{5}{6}\) | |
| \(\dfrac{5\pi}{6}\) | |
| \(\dfrac{8}{15}\) | |
| \(\dfrac{8\pi}{15}\) |
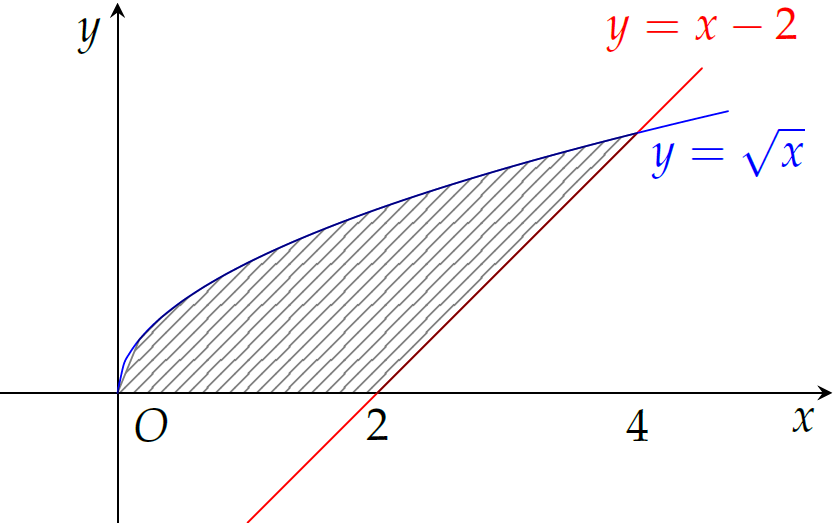
Tính diện tích \(S\) của hình phẳng (phần gạch sọc) trong hình.
| \(S=\dfrac{8}{3}\) | |
| \(S=\dfrac{10}{3}\) | |
| \(S=\dfrac{11}{3}\) | |
| \(S=\dfrac{7}{3}\) |
Một mảnh vườn hình elip có độ dài trục lớn $8$m và độ dài trục nhỏ $6$m. Người ta cần trồng rau trên dải đất rộng $4$m như hình vẽ.
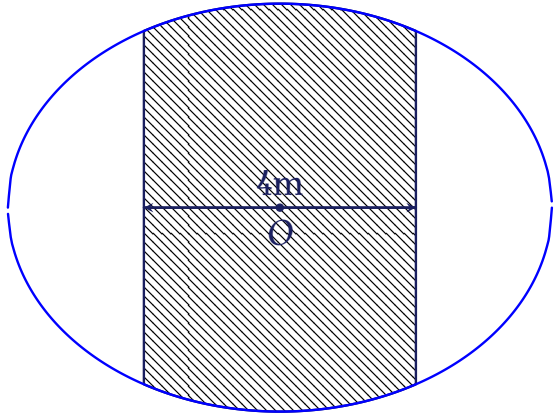
Hỏi cần bao nhiêu tiền để trồng rau trên dải đất đó, biết rằng kinh phí trồng rau là $70000$ đồng/m$^2$?
| $1.607.107$ đồng | |
| $803.553$ đồng | |
| $267.851$ đồng | |
| $2.638.938$ đồng |
Cho hàm số bậc bốn $y=f(x)$. Biết rằng hàm số $g(x)=\ln f(x)$ có bảng biến thiên như sau:
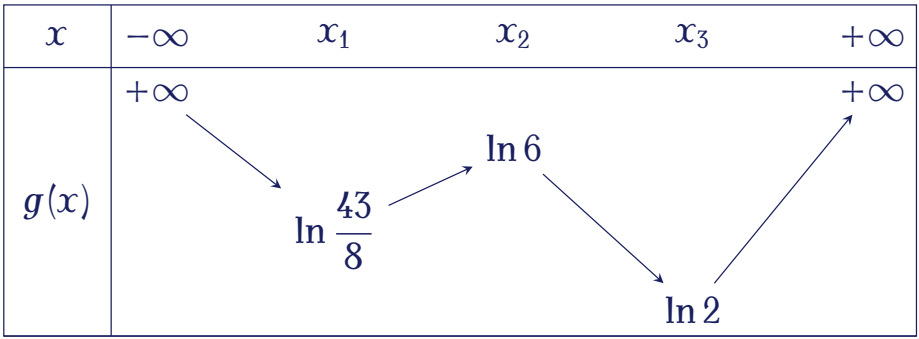
Diện tích hình phẳng giới hạn bởi các đường $y=f'(x)$ và $y=g'(x)$ thuộc khoảng nào dưới đây?
| $(5;6)$ | |
| $(4;5)$ | |
| $(2;3)$ | |
| $(3;4)$ |
