Cho ba số phức \(z_1,\,z_2,\,z_3\) phân biệt thỏa mãn \(\left|z_1\right|=\left|z_2\right|=\left|z_3\right|=3\) và \(\overline{z_1}+\overline{z_2}=\overline{z_3}\). Biết \(z_1,\,z_2,\,z_3\) lần lượt được biểu diễn bởi các điểm \(A,\,B,\,C\) trên mặt phẳng phức. Tính góc \(\widehat{ACB}\).

	\(150^\circ\)
	\(90^\circ\)
	\(120^\circ\)
	\(45^\circ\)

Trong mặt phẳng \(Oxy\), cho tam giác \(ABC\) biết \(A(1;3)\), \(B(-2;-2)\) và \(C(3;1)\). Tính cosin góc \(A\) của tam giác \(ABC\).

	\(\cos A=\dfrac{2}{\sqrt{17}}\)
	\(\cos A=\dfrac{1}{\sqrt{17}}\)
	\(\cos A=-\dfrac{2}{\sqrt{17}}\)
	\(\cos A=-\dfrac{1}{\sqrt{17}}\)

Trong mặt phẳng \(Oxy\), cho hai điểm \(M(-2;-1)\) và \(N(3;-1)\). Tính số đo góc \(\widehat{MON}\).

	\(\dfrac{\sqrt{2}}{2}\)
	\(-\dfrac{\sqrt{2}}{2}\)
	\(-135^\circ\)
	\(135^\circ\)

Trong mặt phẳng \(Oxy\), góc giữa hai vectơ \(\vec{a}=(4;3)\) và \(\vec{b}=(-1;-7)\) có số đo bằng

	\(135^\circ\)
	\(45^\circ\)
	\(30^\circ\)
	\(60^\circ\)

Trong mặt phẳng \(Oxy\), cho \(\vec{a}=(2;5)\) và \(\vec{b}=(3;-7)\). Tính góc giữa hai vectơ \(\vec{a}\) và \(\vec{b}\).

	\(60^\circ\)
	\(45^\circ\)
	\(135^\circ\)
	\(120^\circ\)

Trong không gian cho hai vectơ $\overrightarrow{u}$, $\overrightarrow{v}$ tạo với nhau một góc $60^\circ$, $\left|\overrightarrow{u}\right|=2$ và $\left|\overrightarrow{v}\right|=3$. Tích vô hướng $\overrightarrow{u}\cdot\overrightarrow{v}$ bằng

	$3$
	$6$
	$2$
	$3\sqrt{3}$

Độ dài của vectơ \(\vec{u}=(5;-12)\) bằng

	\(-7\)
	\(13\)
	\(\pm13\)
	\(169\)

Trong mặt phẳng \(Oxy\), cho \(\vec{a}=(-3;4)\), \(\vec{b}=(4;3)\). Kết luận nào sau đây sai?

	\(\left|\vec{a}\right|=\left|\vec{b}\right|\)
	\(\vec{a},\,\vec{b}\) cùng phương
	\(\vec{a}\bot\vec{b}\)
	\(\vec{a}\cdot\vec{b}=0\)

Trong mặt phẳng \(Oxy\), cho vectơ \(\vec{a}=(3;-4)\). Đẳng thức nào sau đây đúng?

	\(\left|\vec{a}\right|=5\)
	\(\left|\vec{a}\right|=3\)
	\(\left|\vec{a}\right|=4\)
	\(\left|\vec{a}\right|=7\)

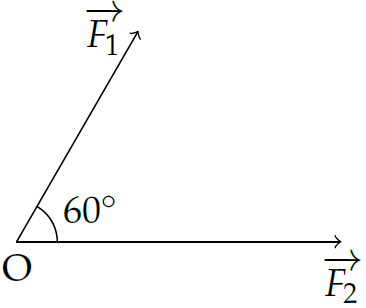
Hai lực \(\overrightarrow{F_1}\) và \(\overrightarrow{F_2}\) có điểm đặt là \(O\). Biết \(\overrightarrow{F_1}\) và \(\overrightarrow{F_2}\) lần lượt có cường độ bằng \(30\)N và \(40\)N. Góc hợp bởi \(\overrightarrow{F_1}\) và \(\overrightarrow{F_2}\) là \(60^\circ\). Tính cường độ lực tổng hợp \(\vec{F}=\overrightarrow{F_1}+\overrightarrow{F_2}\).

	\(50\)N
	\(10\sqrt{13}\)N
	\(35\sqrt{3}\)N
	\(10\sqrt{37}\)N

Cho \(\vec{u}=\vec{a}+3\vec{b}\) vuông góc với \(\vec{v}=7\vec{a}-5\vec{b}\) và \(\vec{x}=\vec{a}-4\vec{b}\) vuông góc với \(\vec{y}=7\vec{a}-2\vec{b}\). Khi đó góc giữa hai vectơ \(\vec{a}\) và \(\vec{b}\) bằng.

	\(\left(\vec{a},\vec{b}\right)=75^\circ\)
	\(\left(\vec{a},\vec{b}\right)=60^\circ\)
	\(\left(\vec{a},\vec{b}\right)=120^\circ\)
	\(\left(\vec{a},\vec{b}\right)=45^\circ\)

Trong không gian \(Oxyz\), cho hai vectơ \(\vec{a}=(-3;4;0)\), \(\vec{b}=(5;0;12)\). Tính cosin góc giữa \(\vec{a}\) và \(\vec{b}\).

	\(\dfrac{3}{13}\)
	\(-\dfrac{3}{13}\)
	\(-\dfrac{5}{6}\)
	\(\dfrac{5}{6}\)

Trong không gian \(Oxyz\), cho hai vectơ \(\vec{u}=(-1;1;0)\), \(\vec{v}=(0;-1;0)\). Góc giữa \(\vec{u}\) và \(\vec{v}\) có số đo bằng

	\(120^\circ\)
	\(45^\circ\)
	\(135^\circ\)
	\(60^\circ\)

Cho trục tọa độ $\left(O,\overrightarrow{e}\right)$. Khẳng định nào sau đây luôn đúng?

	$AB=\overline{AB}$
	$\overrightarrow{AB}=\overline{AB}\cdot\overrightarrow{e}$
	Điểm $M$ có tọa độ là $a$ với trục tọa độ $\left(O,\overrightarrow{e}\right)$ thì $\left|\overrightarrow{OM}\right|=a$
	$\left|\overrightarrow{AB}\right|=\overline{AB}$

Cặp vectơ nào sau đây vuông góc với nhau?

	\(\vec{a}=(1;5)\) và \(\vec{b}=(5;-1)\)
	\(\vec{u}=(1;5)\) và \(\vec{v}=(-5;-1)\)
	\(\vec{m}=(1;5)\) và \(\vec{n}=(5;1)\)
	\(\vec{x}=(1;5)\) và \(\vec{w}=(1;-5)\)

Cặp đường thẳng nào sau đây vuông góc với nhau?

	\(\Delta_1\colon3x-4y+5=0\) và \(\Delta_2\colon-2x+y+3=0\)
	\(\Delta_1\colon x=2019\) và \(\Delta_2\colon y=2020\)
	\(\Delta_1\colon4x-2y+5=0\) và \(\Delta_2\colon-2x+y+3=0\)
	\(\Delta_1\colon\begin{cases}x=1+2t\\ y=2-t\end{cases}\) và \(\Delta_2\colon x+2y-5=0\)

Tính số đo góc giữa hai đường thẳng \(\Delta_1\colon3x-4y+5=0\) và \(\Delta_2\colon-2x+y+3=0\).

	\(63^\circ26'\)
	\(26^\circ63'\)
	\(153^\circ26'\)
	\(26^\circ34'\)

Cho tam giác \(ABC\) có \(A(5;3)\), \(B(2;-1)\), \(C(-1;5)\). Tìm tọa độ trực tâm \(H\) của tam giác \(ABC\).

	\(H(-3;2)\)
	\(H(-3;-2)\)
	\(H(3;2)\)
	\(H(3;-2)\)

Cho vectơ \(\vec{a}=(1;-2)\). Với giá trị nào của \(y\) thì vectơ \(\vec{b}=(-3;y)\) vuông góc với \(\vec{a}\)?

	\(-6\)
	\(6\)
	\(-\dfrac{3}{2}\)
	\(3\)

Trong mặt phẳng \(Oxy\), cho ba điểm \(A(3;6)\), \(B(x;-2)\) và \(C(2;y)\). Tính \(\overrightarrow{OA}\cdot\overrightarrow{BC}\) theo \(x\) và \(y\).

	\(\overrightarrow{OA}\cdot\overrightarrow{BC}=-3x+6y+12\)
	\(\overrightarrow{OA}\cdot\overrightarrow{BC}=0\)
	\(\overrightarrow{OA}\cdot\overrightarrow{BC}=-3x+6y+18\)
	\(\overrightarrow{OA}\cdot\overrightarrow{BC}=3x+6y-12\)