Tam giác $ABC$ có độ dài ba cạnh lần lượt là $21$cm, $17$cm và $10$cm. Tính diện tích tam giác.

	$S=16\text{ cm}^2$
	$S=24\text{ cm}^2$
	$S=48\text{ cm}^2$
	$S=84\text{ cm}^2$

Một mảnh vườn hình tam giác có ba cạnh là \(13\)m, \(14\)m và \(15\)m. Diện tích mảnh vườn đó bằng

	\(84\)m\(^2\)
	\(84\)m
	\(\sqrt{84}\)m\(^2\)
	\(\sqrt{168}\)m\(^2\)

Tam giác \(ABC\) có \(a=8\), \(b=7\), \(c=5\). Diện tích của tam giác \(ABC\) bằng

	\(5\sqrt{3}\)
	\(8\sqrt{3}\)
	\(10\sqrt{3}\)
	\(12\sqrt{3}\)

Tam giác $HPS$ đều, cạnh $PS=a\sqrt{2}$. $S_{HPS}$ bằng

	$a^2\dfrac{\sqrt{3}}{4}$
	$a^2\dfrac{\sqrt{6}}{4}$
	$a^2\dfrac{\sqrt{3}}{2}$
	$a^2\dfrac{\sqrt{6}}{2}$

Cho \(\triangle ABC\) có ba cạnh lần lượt là \(a,\,b,\,c\). Công thức tính diện tích \(\triangle ABC\) là

	\(S=\dfrac{a\cdot b\cdot c}{2R}\)
	\(S=p\cdot R\)
	\(S=\dfrac{1}{2}a\cdot b\cdot\cos C\)
	\(S=\dfrac{1}{2}a\cdot c\cdot\sin B\)

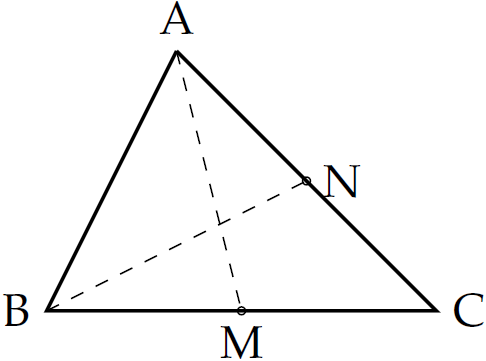
Bạn Thùy đặt một tấm bìa cứng hình tam giác (như hình vẽ) lên đầu một ngòi bút nhưng tấm bìa không bị rơi. Hỏi bạn Thùy đã đặt ngòi bút tại điểm nào của tấm bìa?

	Điểm \(A\)
	Trung điểm \(M\)
	Trung điểm \(N\)
	Giao điểm \(AM\) và \(BN\)

Cho tam giác \(ABC\). Kết quả nào sau đây không đúng?

	\(S=\dfrac{abc}{2R}\)
	\(S=\dfrac{1}{2}ac\sin B\)
	\(S=\dfrac{a+b+c}{2}r\)
	\(S=\sqrt{p(p-a)(p-b)(p-c)}\)

Tam giác \(ABC\) có \(AB=8\)cm, \(AC=18\)cm và diện tích bằng \(64\)cm\(^2\). Giá trị \(\sin A\) là

	\(\dfrac{\sqrt{3}}{2}\)
	\(\dfrac{3}{8}\)
	\(\dfrac{4}{5}\)
	\(\dfrac{8}{9}\)

Một tam giác có ba cạnh là \(26\), \(28\), \(30\). Bán kính vòng tròn nội tiếp là

	\(16\)
	\(8\)
	\(4\)
	\(4\sqrt{2}\)

Hai chiếc tàu thủy cùng xuất phát từ vị trí \(A\), đi thẳng theo hai hướng tạo với nhau một góc \(60^\circ\). Tàu thứ nhất chạy với tốc độ \(30\)km/h, tàu thứ hai chạy với tốc độ \(40\)km/h. Hỏi sau \(2\) giờ, khoảng cách giữa hai chiếc tàu là bao nhiêu km?

	\(10\sqrt{13}\)
	\(15\sqrt{13}\)
	\(20\sqrt{13}\)
	\(15\)

Cho tam giác \(ABC\) có diện tích \(S\). Gọi \(M,\,N\) là hai điểm thỏa mãn \(\overrightarrow{AM}=2\overrightarrow{AB}\), \(\overrightarrow{CN}=-2\overrightarrow{AC}\). Tính diện tích \(\Delta AMN\) theo \(S\).

	\(2S\)
	\(8S\)
	\(4S\)
	\(6S\)

Tam giác đều nội tiếp đường tròn bán kính \(R=4\)cm có diện tích là

	\(12\sqrt{3}\)cm\(^2\)
	\(13\sqrt{2}\)cm\(^2\)
	\(13\)cm\(^2\)
	\(15\)cm\(^2\)

Cho tam giác \(ABC\) có \(a=4\), \(c=5\), \(\widehat{B}=150^\circ\). Tính diện tích tam giác \(ABC\).

	\(S=10\)
	\(S=10\sqrt{3}\)
	\(S=5\)
	\(S=5\sqrt{3}\)

Cho tam giác \(ABC\) có \(b=7\), \(c=5\), \(\cos A=\dfrac{3}{5}\). Đường cao \(h_a\) của tam giác \(ABC\) là

	\(8\)
	\(\dfrac{7\sqrt{2}}{2}\)
	\(80\sqrt{3}\)
	\(8\sqrt{3}\)

Cho tam giác \(ABC\) với \(a,\,b,\,c\) lần lượt là độ dài các cạnh \(BC\), \(CA\), \(AB\). Chọn mệnh đề sai trong các mệnh đề sau:

	\(a^2=b^2+c^2-2bc\cos A\)
	\(m_a^2=\dfrac{b^2+c^2}{2}-\dfrac{a^2}{4}\)
	\(S=\dfrac{1}{2}ab\cos C\)
	\(\cos A=\dfrac{b^2+c^2-a^2}{2bc}\)

Tam giác \(ABC\) có \(\widehat{A}=60^\circ\), \(b=10\), \(c=20\). Diện tích của tam giác \(ABC\) bằng

	\(50\sqrt{3}\)
	\(50\)
	\(50\sqrt{2}\)
	\(50\sqrt{5}\)

Cho \(\triangle ABC\) có các cạnh \(BC=a\), \(AC=b\), \(AB=c\). Diện tích của \(\triangle ABC\) là

	\(S=\dfrac{1}{2}ac\sin C\)
	\(S=\dfrac{1}{2}bc\sin B\)
	\(S=\dfrac{1}{2}ac\sin B\)
	\(S=\dfrac{1}{2}bc\sin C\)

Một mảnh vườn hình elip có độ dài trục lớn $8$m và độ dài trục nhỏ $6$m. Người ta cần trồng rau trên dải đất rộng $4$m như hình vẽ.

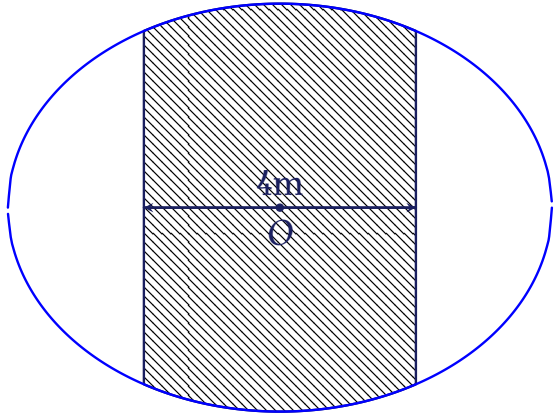
Hỏi cần bao nhiêu tiền để trồng rau trên dải đất đó, biết rằng kinh phí trồng rau là $70000$ đồng/m$^2$?

	$1.607.107$ đồng
	$803.553$ đồng
	$267.851$ đồng
	$2.638.938$ đồng

Ông An muốn làm cửa rào sắt có hình dạng và kích thước như hình vẽ bên, biết đường cong phía trên là một Parabol. Giá $1m^2$ của rào sắt là $700 000$ đồng.

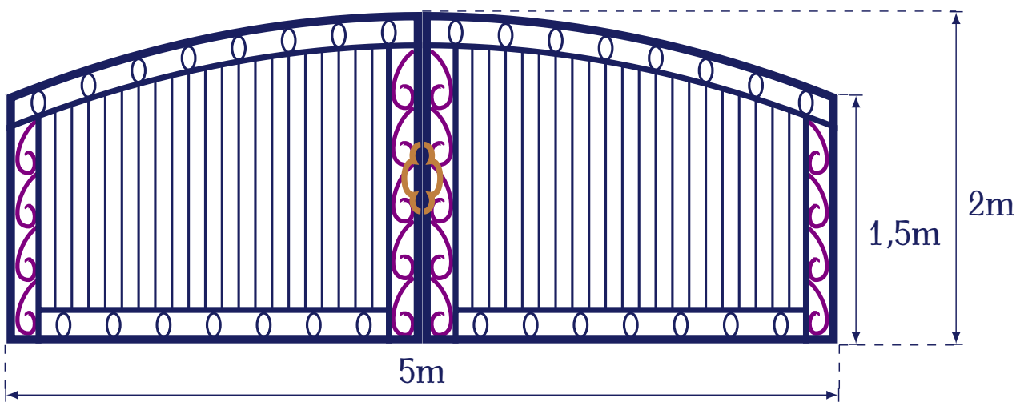
Hỏi ông An phải trả bao nhiêu tiền để làm cái cửa sắt như vậy (làm tròn đến hàng phần nghìn).

(Cảm ơn tác giả đã vẽ hình và trình bày, cảm ơn TS. Trần Lê Nam đã chia sẻ)

	$6 520 000$ đồng
	$6 320 000$ đồng
	$6 417 000$ đồng
	$6 620 000$ đồng

Một khung cửa kính hình parabol với đỉnh $M$ và cạnh đáy $AB$ như minh họa ở hình bên. Biết chi phí để lắp phần kính màu (phần tô đậm trong hình) là $200.000$ đồng/m$^2$ và phần kính trắng còn lại là $150.000$ đồng/m$^2$.

Cho $MN=AB=4$m và $MC=CD=DN$. Hỏi số tiền để lắp kính cho khung cửa như trên gần nhất với số tiền nào dưới đây?

	$1.954.000$ đồng
	$2.123.000$ đồng
	$1.946.000$ đồng
	$2.145.000$ đồng