Điểm \(M\) trong hình vẽ bên biểu diễn số phức \(z\). Tìm phần thực và phần ảo của \(z\).
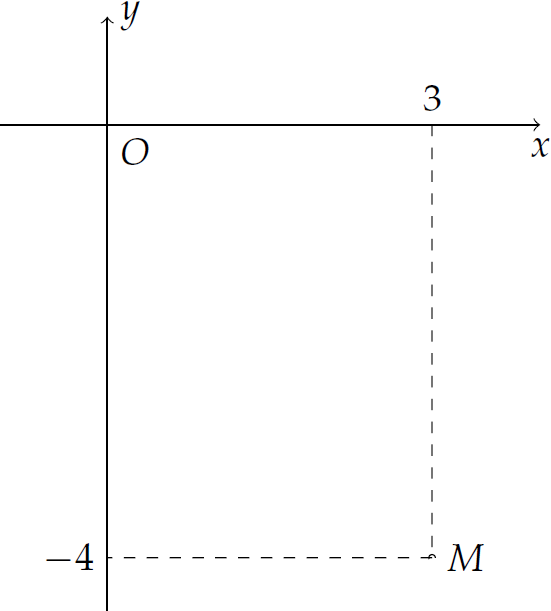
| \(-4\) và \(3\) | |
| \(3\) và \(-4\mathrm{i}\) | |
| \(3\) và \(-4\) | |
| \(-4\) và \(3\mathrm{i}\) |
Điểm $A$ trong hình vẽ bên biểu diễn cho số phức $z$. Mệnh đề nào sau đây đúng?
| Phần thực là $-3$, phần ảo là $2$ | |
| Phần thực là $-3$, phần ảo là $2i$ | |
| Phần thực là $3$, phần ảo là $-2i$ | |
| Phần thực là $3$, phần ảo là $2$ |
Điểm $M$ trong hình vẽ bên là điểm biểu diễn cho số phức $z$.
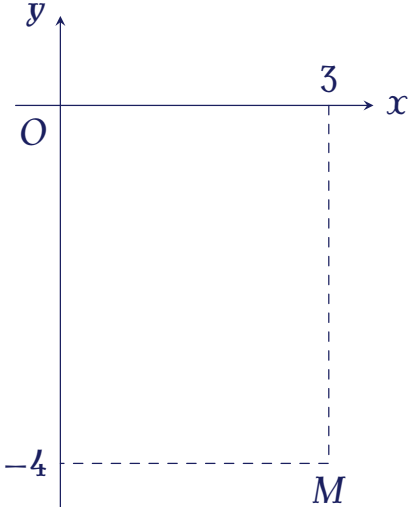
Phần ảo của số phức $(1+i)z$ bằng
| $7$ | |
| $-7$ | |
| $-1$ | |
| $1$ |
Trên mặt phẳng $Oxy$, cho các điểm như hình bên.
Điểm biểu diễn số phức $z=-3+2i$ là
| điểm $N$ | |
| điểm $Q$ | |
| điểm $M$ | |
| điểm $P$ |
Cho số phức $z$ thỏa mãn điều kiện $2\overline{z}=z+2-3i$.
Số phức $z$ có điểm biểu diễn là điểm nào trong các điểm $M,\,N,\,P,\,Q$ ở hình trên?
| $M$ | |
| $Q$ | |
| $P$ | |
| $N$ |
Điểm nào trong hình vẽ dưới đây là điểm biểu diễn của số phức $z=\dfrac{i-3}{1+i}$?

| Điểm $B$ | |
| Điểm $C$ | |
| Điểm $A$ | |
| Điểm $D$ |
Gọi $z,\,w$ là các số phức có điểm biểu diễn lần lượt là $M$ và $N$ trên mặt phẳng $Oxy$ như hình minh họa bên.
Phần ảo của số phức $\dfrac{z}{w}$ là
| $\dfrac{14}{17}$ | |
| $3$ | |
| $-\dfrac{5}{17}$ | |
| $-\dfrac{1}{2}$ |
Điểm nào trong hình bên biểu diễn cho số phức $w=4-i$?
| Điểm $M$ | |
| Điểm $N$ | |
| Điểm $P$ | |
| Điểm $Q$ |
Điểm $M$ trong hình vẽ bên là điểm biểu diễn của số phức nào dưới đây?
| $z=-2+3i$ | |
| $z=3+2i$ | |
| $z=2-3i$ | |
| $z=3-2i$ |
Trong mặt phẳng $Oxy$, số phức $z=-2+4i$ được biểu diễn bởi điểm nào trong các điểm ở hình vẽ dưới đây?
| Điểm $D$ | |
| Điểm $B$ | |
| Điểm $C$ | |
| Điểm $A$ |
Điểm nào trong hình vẽ bên là điểm biểu diễn số phức $z=-1+2i$?
| $N$ | |
| $P$ | |
| $M$ | |
| $Q$ |
Trên mặt phẳng tọa độ, biết \(M\left(-3;1\right)\) là điểm biểu diễn số phức \(z\). Phần thực của \(z\) bằng
| \(1\) | |
| \(-3\) | |
| \(-1\) | |
| \(3\) |
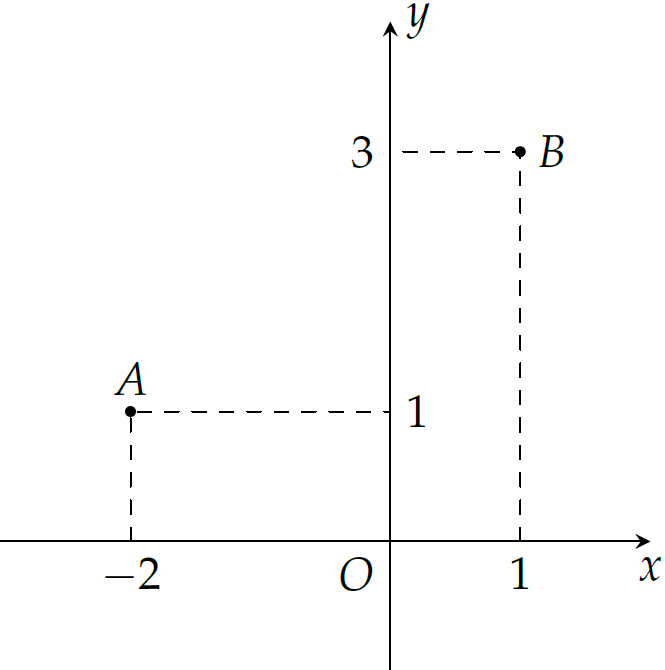
Trong mặt phẳng \(Oxy\), cho các điểm \(A,\,B\) như hình vẽ trên. Trung điểm của đoạn thẳng \(AB\) biểu diễn số phức
| \(-\dfrac{1}{2}+2i\) | |
| \(2-\dfrac{1}{2}i\) | |
| \(-1+2i\) | |
| \(2-i\) |
Kí hiệu \(z_0\) là nghiệm phức có phần ảo dương của phương trình \(2z^2-6z+15=0\). Trên mặt phẳng tọa độ, tìm tọa độ của điểm \(M\) biểu diễn số phức \(z_0\).
| \(M\left(-\dfrac{3}{2};\dfrac{\sqrt{21}}{2}i\right)\) | |
| \(M\left(-\dfrac{3}{2};\dfrac{\sqrt{21}}{2}\right)\) | |
| \(M\left(\dfrac{3}{2};\dfrac{\sqrt{21}}{2}\right)\) | |
| \(M\left(\dfrac{3}{2};\dfrac{\sqrt{21}}{2}i\right)\) |
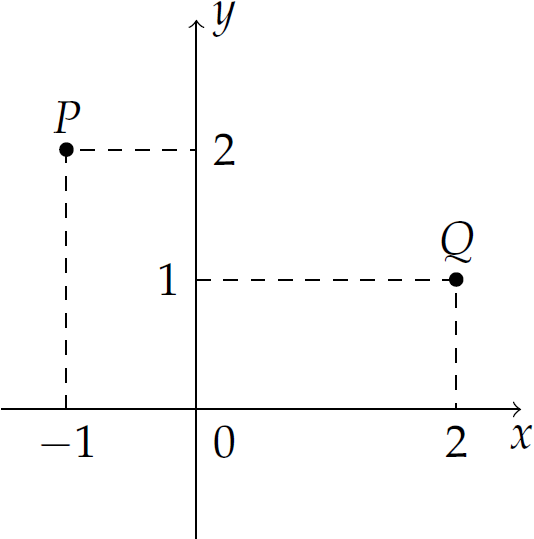
Trong hình vẽ, điểm \(P\) biểu diễn số phức \(z_1\), điểm \(Q\) biểu diễn số phức \(z_2\). Tìm số phức \(z=z_1+z_2\).
| \(z=1+3\mathrm{i}\) | |
| \(z=-3+\mathrm{i}\) | |
| \(z=-1+2\mathrm{i}\) | |
| \(z=2+\mathrm{i}\) |
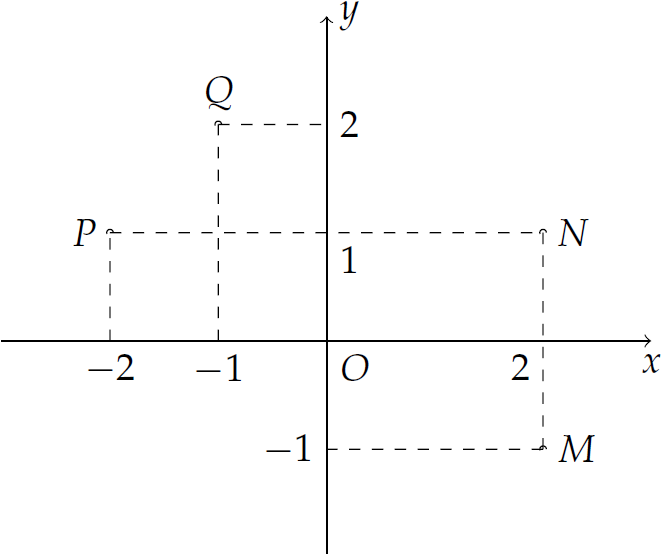
Điểm nào trong hình vẽ là điểm biểu diễn số phức \(z=-1+2\mathrm{i}\)?
| \(N\) | |
| \(P\) | |
| \(M\) | |
| \(Q\) |
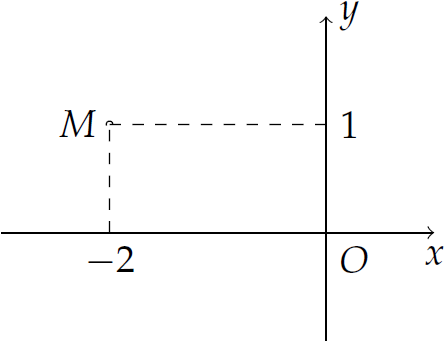
Điểm \(M\) trong hình vẽ bên biểu diễn số phức nào trong các số phức cho sau đây?
| \(z=-2+\mathrm{i}\) | |
| \(z=1-2\mathrm{i}\) | |
| \(z=2+\mathrm{i}\) | |
| \(z=1+2\mathrm{i}\) |
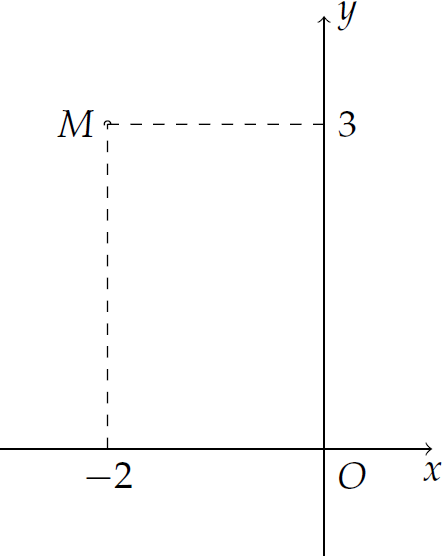
Điểm \(M\) trong hình vẽ bên biểu diễn số phức nào trong các số phức cho sau đây?
| \(3-2\mathrm{i}\) | |
| \(-2+3\mathrm{i}\) | |
| \(2-3\mathrm{i}\) | |
| \(3+2\mathrm{i}\) |
Gọi $z_1,\,z_2$ là hai nghiệm phức của phương trình $z^2-6z+14=0$ và $M,\,N$ lần lượt là điểm biểu diễn của $z_1,\,z_2$ trên mặt phẳng tọa độ. Trung điểm của đoạn $MN$ có tọa độ là
| $(3;7)$ | |
| $(-3;0)$ | |
| $(3;0)$ | |
| $(-3;7)$ |
Gọi $A,\,B,\,C$ là điểm biểu diễn cho các số phức $z_1=-2+3i$, $z_2=-4-2i$, $z_3=3+i$. Khi đó tọa độ trọng tâm $G$ của tam giác $ABC$ là
| $\left(-1;-\dfrac{2}{3}\right)$ | |
| $\left(-1;\dfrac{2}{3}\right)$ | |
| $\left(1;-\dfrac{2}{3}\right)$ | |
| $\left(1;\dfrac{2}{3}\right)$ |
