Tìm các giá trị của tham số \(m\) để đường cong \(\left(\mathscr{C}\right)\colon y=x^3-3x+m\) cắt trục hoành tại \(3\) điểm phân biệt.
| \(m\in(2;+\infty)\) | |
| \(m\in(-2;2)\) | |
| \(m\in\mathbb{R}\) | |
| \(m\in(-\infty;-2)\) |
Tìm các giá trị của tham số \(m\) để phương trình \(x^3-12x+m-2=0\) có \(3\) nghiệm phân biệt.
| \(m\in[-14;18]\) | |
| \(m\in(-14;18)\) | |
| \(m\in(-18;14)\) | |
| \(\left[\begin{array}{l}m<-14\\ m>18\end{array}\right.\) |
Số giao điểm của đồ thị hàm số \(y=-2x^3-3x^2+1\) với trục hoành là
| \(1\) | |
| \(0\) | |
| \(3\) | |
| \(2\) |
Số giao điểm của đồ thị hàm số \(y=x^3-3x+1\) và trục hoành là
| \(3\) | |
| \(0\) | |
| \(2\) | |
| \(1\) |
Đồ thị của hàm số nào dưới đây cắt trục hoành tại $3$ điểm phân biệt?
| $y=x^3-3x+3$ | |
| $y=x^3+3x+1$ | |
| $y=-x^3+3x+5$ | |
| $y=x^3-3x+1$ |
Có bao nhiêu giá trị nguyên của tham số a thuộc đoạn $[-10;10]$ để hàm số $$y=\big|-x^3+3(a+1)x^2-3a(a+2)x+a^2(a+3)\big|$$đồng biến trên khoảng $(0;1)$
| $21$ | |
| $10$ | |
| $8$ | |
| $2$ |
Có bao nhiêu giá trị nguyên của tham số $a\in(-10;+\infty)$ để hàm số $y=\big|x^3+(a+2)x+9-a^2\big|$ đồng biến trên khoảng $(0;1)$?
| $12$ | |
| $11$ | |
| $6$ | |
| $5$ |
Cho hàm số bậc ba $y=f(x)$ có đồ thị là đường cong trong hình bên.
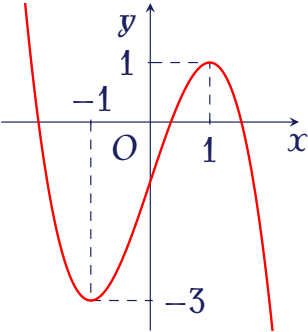
Có bao nhiêu giá trị nguyên của tham số $m$ để phương trình $f(x)=m$ có ba nghiệm thực phân biệt?
| $2$ | |
| $5$ | |
| $3$ | |
| $4$ |
Đồ thị của hàm số nào dưới đây cắt trục hoành tại $3$ điểm phân biệt?
| $y=x^3-3x+3$ | |
| $y=x^3+3x+1$ | |
| $y=-x^3+3x+5$ | |
| $y=x^3-3x+1$ |
Tìm tất cả các giá trị thực của tham số $m$ sao cho hàm số $y=\dfrac{mx^3}{3}+7mx^2+14x-m+2$ nghịch biến trên $[1;+\infty)$.
| $\left(-\infty;-\dfrac{14}{15}\right)$ | |
| $\left(-\infty;-\dfrac{14}{15}\right]$ | |
| $\left[-2;-\dfrac{14}{15}\right]$ | |
| $\left[-\dfrac{14}{15};+\infty\right)$ |
Tìm tập hợp giá trị của tham số $m$ để hàm số $y=x^3-mx^2-(m-6)x+1$ đồng biến trên khoảng $(0;4)$.
| $(-\infty;6]$ | |
| $(-\infty;3]$ | |
| $(-\infty;3)$ | |
| $[3;6]$ |
Cho hàm số $f\left(x\right)=x^3-2x^2+mx-3$ . Tìm $m$ để $f'\left(x\right)< 0$ với mọi $x\in\left(0;2\right)$.
Cho hàm số $y=x^4-4x^2+m$. Tìm $m$ để đồ thị của hàm số cắt trục hoành tại $4$ điểm phân biệt sao cho hình phẳng giới hạn bởi đồ thị với trục hoành có diện tích phần phía trên trục hoành bằng diện tích phần phía dưới trục hoành. Khi đó $m=\dfrac{a}{b}$ với $\dfrac{a}{b}$ là phân số tối giản. Tính $a+2b$.
| $37$ | |
| $38$ | |
| $0$ | |
| $29$ |
Tìm \(m\) để đường thẳng \(y=x-m\) cắt đồ thị hàm số \(y=\dfrac{2x+1}{x+1}\) tại \(2\) điểm phân biệt.
| \(m<-1\) | |
| \(m>-5\) | |
| \(m<-5\) hoặc \(m>-1\) | |
| \(-5< m<-1\) |
Tìm \(m\) để đường thẳng \(y=2x+m\) cắt đồ thị hàm số \(y=\dfrac{2x}{x+1}\) tại \(2\) điểm phân biệt.
| \(m\in(-\infty;0)\cup(8;+\infty)\) | |
| \(m\in(-\infty;0]\cup[8;+\infty)\) | |
| \(m\in(0;8)\) | |
| \(m\in[0;8]\) |
Cho hàm số \(y=f(x)\) xác định, liên tục trên \(\mathbb{R}\) và có bảng biến thiên như sau:
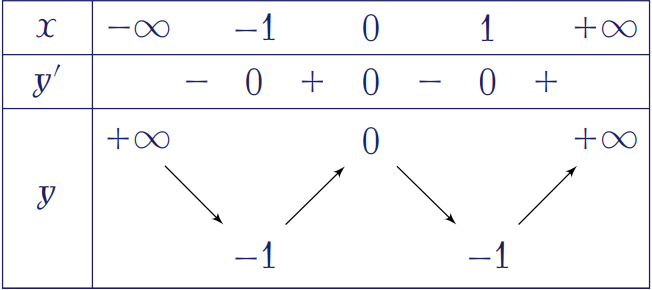
Tìm tất cả các giá trị thực của tham số \(m\) để phương trình \(f(x)-1=m\) có đúng \(2\) nghiệm.
| \(-2< m<-1\) | |
| \(m=-2\) hoặc \(m\geq-1\) | |
| \(m=-1\) hoặc \(m>0\) | |
| \(m=-2\) hoặc \(m>-1\) |
Cho hàm số \(y=f(x)\) xác định trên \(\mathbb{R}\setminus\{0\}\), liên tục trên từng khoảng xác định và có bảng biến thiên như hình.

Tìm tập hợp các giá trị thực của tham số \(m\) để phương trình \(f(x)=m\) có \(3\) nghiệm phân biệt.
| \([-2;2)\) | |
| \((-2;2)\) | |
| \((-2;2]\) | |
| \([2;+\infty)\) |
Cho hàm số \(y=f(x)\) xác định trên \(\mathbb{R}\setminus\{0\}\), liên tục trên từng khoảng xác định và có bảng biến thiên như hình.
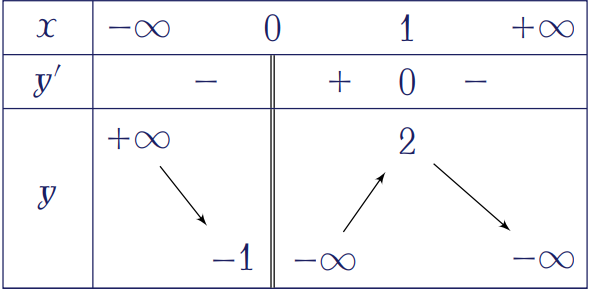
Phương trình \(f(x)=m\) với \(m\in(-1;2)\) có bao nhiêu nghiệm?
| \(3\) | |
| \(1\) | |
| \(0\) | |
| \(2\) |
Cho hàm số \(y=f(x)\) xác định, liên tục trên \(\mathbb{R}\) và có bảng biến thiên như sau:

Tìm tất cả các giá trị thực của tham số \(m\) để phương trình \(f(x)-m=0\) có \(3\) nghiệm phân biệt.
| \(-3\leq m\leq2\) | |
| \(-3< m<2\) | |
| \(-4\leq m\leq2\) | |
| \(-4< m<2\) |
Cho hàm số \(y=f(x)\) xác định, liên tục trên \(\mathbb{R}\) và có bảng biến thiên như sau:

Tập hợp các giá trị thực của tham số \(m\) để phương trình \(f(x)=m\) có đúng một nghiệm là
| \((-\infty;-2)\cup(2;+\infty)\) | |
| \((-\infty;-2]\cup[2;+\infty)\) | |
| \((-2;2)\) | |
| \([-2;2]\) |
