Một gia đình cần khoan một cái giếng để lấy nước. Họ thuê một đội khoan giếng đến để khoan giếng nước. Giá của mét khoan đầu tiên là \(80.000\) đồng, kể từ mét khoan thứ hai trở đi, giá của mỗi mét khoan tăng thêm \(5.000\) đồng so với giá của mét khoan trước đó. Biết rằng cần phải khoan sâu xuống \(50\) mét mới có nước. Vậy phải trả bao nhiêu tiền để khoan cái giếng đó?
| \(5.250.000\) đồng | |
| \(10.125.000\) đồng | |
| \(4.000.000\) đồng | |
| \(4.245.000\) đồng |
Tính tổng $$T=1000^2-999^2+998^2-997^2+\cdots+2^2-1^2$$
| \(T=500500\) | |
| \(T=500005\) | |
| \(T=505000\) | |
| \(T=500050\) |
Tính \(T=15+20+25+\cdots+7515\).
| \(T=5651265\) | |
| \(T=5651256\) | |
| \(T=5651625\) | |
| \(T=5651526\) |
Cho cấp số cộng \(\left(u_n\right)\) thỏa mãn \(u_2+u_{23}=60\). Tính tổng \(S_{24}\) của \(24\) số hạng đầu tiên của cấp số cộng đã cho.
| \(S_{24}=60\) | |
| \(S_{24}=120\) | |
| \(S_{24}=720\) | |
| \(S_{24}=1440\) |
Cho cấp số cộng \(\left(u_n\right)\) thỏa mãn \(u_2+u_8+u_9+u_{15}=100\). Tính tổng \(16\) số hạng đầu tiên của \(\left(u_n\right)\).
| \(S_{16}=100\) | |
| \(S_{16}=200\) | |
| \(S_{16}=300\) | |
| \(S_{16}=400\) |
Tổng \(n\) số hạng đầu tiên của một cấp số cộng là \(S_n=n^2+4n\) với \(n\in\mathbb{N}^*\). Tìm số hạng tổng quát \(u_n\) của cấp số cộng đã cho.
| \(u_n=2n+3\) | |
| \(u_n=3n+2\) | |
| \(u_n=5\cdot3^{n-1}\) | |
| \(u_n=5\cdot\left(\dfrac{8}{5}\right)^{n-1}\) |
Tổng \(n\) số hạng đầu tiên của một cấp số cộng là \(S_n=\dfrac{3n^2-19n}{4}\) với \(n\in\mathbb{N}^*\). Tìm số hạng đầu tiên \(u_1\) và công sai \(d\) của cấp số cộng đã cho.
| \(\begin{cases}u_1=2\\ d=-\dfrac{1}{2}\end{cases}\) | |
| \(\begin{cases}u_1=-4\\ d=\dfrac{3}{2}\end{cases}\) | |
| \(\begin{cases}u_1=-\dfrac{3}{2}\\ d=-2\end{cases}\) | |
| \(\begin{cases}u_1=\dfrac{5}{2}\\ d=\dfrac{1}{2}\end{cases}\) |
Một cấp số cộng có \(12\) số hạng. Biết rằng tổng của \(12\) số hạng đó bằng \(144\) và số hạng thứ \(12\) bằng \(23\). Khi đó công sai \(d\) của cấp số cộng đã cho bằng
| \(2\) | |
| \(3\) | |
| \(4\) | |
| \(5\) |
Một cấp số cộng có số hạng đầu là \(1\), công sai là \(4\), tổng của \(n\) số hạng đầu là \(561\). Khi đó số hạng thứ \(n\) của cấp số cộng đó là
| \(u_n=57\) | |
| \(u_n=61\) | |
| \(u_n=65\) | |
| \(u_n=69\) |
Cho cấp số cộng \(\left(u_n\right)\) có \(d=-2\) và \(S_8=72\). Tìm số hạng đầu \(u_1\).
| \(u_1=16\) | |
| \(u_1=-16\) | |
| \(u_1=\dfrac{1}{16}\) | |
| \(u_1=-\dfrac{1}{16}\) |
Xét các số nguyên dương chia hết cho \(3\). Tổng số \(50\) số nguyên dương đầu tiên đó bằng
| \(7650\) | |
| \(7500\) | |
| \(3900\) | |
| \(3825\) |
Số hạng tổng quát của một cấp số cộng là \(u_n=3n+4\) với \(n\in\mathbb{N}^*\). Gọi \(S_n\) là tổng của \(n\) số hạng đầu tiên của cấp số cộng đã cho. Mệnh đề nào sau đây đúng?
| \(S_n=\dfrac{3^n-1}{2}\) | |
| \(S_n=\dfrac{7\left(3^n-1\right)}{2}\) | |
| \(S_n=\dfrac{3n^2+5n}{2}\) | |
| \(S_n=\dfrac{3n^2+11n}{2}\) |
Cho cấp số cộng \(\left(u_n\right)\) có \(u_1=\dfrac{1}{4}\) và \(d=-\dfrac{1}{4}\). Gọi \(S_5\) là tổng năm số hạng đầu tiên của \(\left(u_n\right)\). Mệnh đề nào sau đây đúng?
| \(S_5=-\dfrac{5}{4}\) | |
| \(S_5=\dfrac{4}{5}\) | |
| \(S_5=\dfrac{5}{4}\) | |
| \(S_5=-\dfrac{4}{5}\) |
Cho cấp số cộng \(\left(u_n\right)\) có \(u_1=4\) và \(d=-5\). Tính tổng \(100\) số hạng đầu tiên của \(\left(u_n\right)\).
| \(S_{100}=24350\) | |
| \(S_{100}=-24350\) | |
| \(S_{100}=-24600\) | |
| \(S_{100}=24600\) |
Cho cấp số cộng \(\left(u_n\right)\) có số hạng đầu \(u_1=2\) và công sai \(d=-3\). Tính tổng \(10\) số hạng đầu của \(\left(u_n\right)\).
| \(S_{10}=115\) | |
| \(S_{10}=-155\) | |
| \(S_{10}=-115\) | |
| \(S_{10}=155\) |
Tính \(S=1+5+9+\cdots+397\).
| \(S=19298\) | |
| \(S=19090\) | |
| \(S=19920\) | |
| \(S=19900\) |
Ông Bụt hạ phàm xuống Mỹ Thuận và tặng nước tiên miễn phí cho mọi người. Người nhanh chân đến trước được Bụt ban cho \(1\) lít nước tiên, và cứ người nào đến sau thì đều được ban một lượng nước tiên bằng \(\dfrac{2}{3}\) của người trước đó. Giả sử số người đến nhận nước tiên là vô hạn thì Bụt có thể ban bao nhiêu lít nước tiên?
| \(3\) | |
| \(\dfrac{2}{3}\) | |
| \(\dfrac{3}{2}\) | |
| \(+\infty\) |
Từ độ cao \(55,8\) m của tháp nghiên Pisa nước Ý, người ta thả một quả bóng cao su xuống đất. Giả sử mỗi lần chạm đất thì quả bóng lại nảy lên độ cao bằng \(\dfrac{1}{10}\) độ cao mà quả bóng đạt trước đó. Tổng độ dài hành trình của quả bóng từ lúc thả cho đến khi nó nằm yên trên mặt đất thuộc khoảng nào sau đây?
| \((67;69)\) | |
| \((60;63)\) | |
| \((64;66)\) | |
| \((69;72)\) |
Một du khách vào trường đua ngựa đặt cược, lần đầu đặt \(20000\) đồng, mỗi lần sau tiền đặt cược gấp đôi lần trước đó. Người này thua \(9\) lần liên tiếp và thắng ở lần thứ \(10\). Hỏi du khách trên thắng hay thua bao nhiêu?
| Hòa vốn | |
| Thua \(20000\) đồng | |
| Thắng \(20000\) đồng | |
| Thua \(40000\) đồng |
Một bình đựng nước dạng hình nón (không có nắp đậy), đựng đầy nước. Biết rằng chiều cao của bình gấp $3$ lần bán kính đáy của nó. Người ta thả vào bình đó một khối trụ và đo được thể tích nước tràn ra ngoài là $\dfrac{16\pi}{9}\text{dm}^3$. Biết rằng một mặt của khối trụ nằm trên mặt đáy của hình nón và khối trụ có chiều cao bằng đường kính đáy của hình nón (hình vẽ).
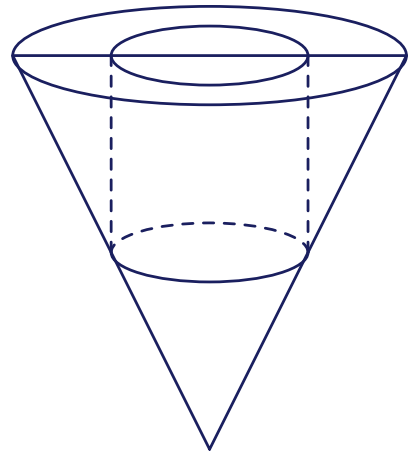
Tính bán kính đáy $R$ của bình nước.
| $R=4$dm | |
| $R=2$dm | |
| $R=3$dm | |
| $R=5$dm |
