Cho hàm số \(y=f(x)\) có đạo hàm liên tục trên \(\mathbb{R}\) và thỏa mãn \(f(2)=16\), \(\displaystyle\int\limits_{0}^{2}f(x)\mathrm{\,d}x=4\). Tính \(I=\displaystyle\int\limits_{0}^{1}xf'(2x)\mathrm{\,d}x\).
| \(I=13\) | |
| \(I=20\) | |
| \(I=12\) | |
| \(I=7\) |
Cho hàm số $f(x)$ liên tục trên $\mathbb{R}$ thỏa $\displaystyle\displaystyle\int\limits_{0}^{1}f(x)\mathrm{d}x=2$ và $\displaystyle\displaystyle\int\limits_{0}^2f(3x+1)\mathrm{d}x=6$. Tính $I=\displaystyle\displaystyle\int\limits_{0}^{7}f(x)\mathrm{d}x$.
| $I=20$ | |
| $I=8$ | |
| $I=18$ | |
| $I=16$ |
Cho $\displaystyle\displaystyle\int\limits_{4}^{9}f(x)\mathrm{d}x=10$. Tính tích phân $J=\displaystyle\displaystyle\int\limits_{0}^{1}f(5x+4)\mathrm{d}x$.
| $J=2$ | |
| $J=10$ | |
| $J=50$ | |
| $J=4$ |
Cho hàm số $f(x)$ liên tục trên $\mathbb{R}$ thỏa mãn $f(x)=3x^2-2x+3+4\displaystyle\int\limits_{0}^{1}xf\left(x^2\right)\mathrm{\,d}x$. Khi đó $\displaystyle\int\limits_{2}^{3}f(x)\mathrm{\,d}x$ bằng
| $17$ | |
| $11$ | |
| $14$ | |
| $21$ |
Cho hàm số $f(x)$ xác định và liên tục trên đoạn $[0;1]$ thỏa mãn $f(x)=x^3+\displaystyle\int\limits_{0}^{1}x^3f\left(x^2\right)\mathrm{\,d}x$, $\forall x\in[0;1]$. Tính tích phân $\displaystyle\int\limits_{0}^{1}f(x)\mathrm{\,d}x$.
| $\dfrac{1}{4}$ | |
| $\dfrac{4}{15}$ | |
| $\dfrac{13}{20}$ | |
| $\dfrac{23}{60}$ |
Biết $f\left(x\right)$ là hàm số liên tục trên $\mathbb{R}$ và $\displaystyle\displaystyle\int\limits_{0}^{9}f\left(x\right)\mathrm{d}x=9$. Khi đó tính $I=\displaystyle\displaystyle\int\limits_{2}^{5}f\left(3x-6\right)\mathrm{d}x$.
| $I=27$ | |
| $I=24$ | |
| $I=3$ | |
| $I=0$ |
Nếu $\displaystyle\displaystyle\int\limits_1^3f(x)\mathrm{\,d}x=3$ thì $\displaystyle\displaystyle\int\limits_1^5f\left(\dfrac{x+1}{2}\right)\mathrm{\,d}x$ bằng
| $\dfrac{3}{2}$ | |
| $3$ | |
| $\dfrac{5}{2}$ | |
| $6$ |
Cho hàm số $f(x)=\begin{cases} x^2-1 &\text{khi }x\geq2\\ x^2-2x+3 &\text{khi }x< 2 \end{cases}$. Tích phân $\displaystyle\displaystyle\int\limits_{0}^{\tfrac{\pi}{2}}f\left(2\sin x+1\right)\cos x\mathrm{\,d}x$ bằng
| $\dfrac{23}{3}$ | |
| $\dfrac{23}{6}$ | |
| $\dfrac{17}{6}$ | |
| $\dfrac{17}{3}$ |
Hàm số \(y=f(x)\) liên tục trên \([1;4]\) và thỏa mãn \(f(x)=\dfrac{f\left(2\sqrt{x}-1\right)}{\sqrt{x}}+\dfrac{\ln x}{x}\). Tính tích phân \(I=\displaystyle\int\limits_{3}^{4}f(x)\mathrm{\,d}x\).
| \(I=3+2\ln^22\) | |
| \(I=\ln^2\) | |
| \(I=2\ln2\) | |
| \(I=2\ln^22\) |
Cho hàm số \(f(x)\) liên tục trên \(\mathbb{R}\), biết \(\displaystyle\int\limits_{0}^{\tfrac{\pi}{4}}f\left(\tan x\right)\mathrm{\,d}x=4\) và \(\displaystyle\int\limits_{0}^{1}\dfrac{x^2\cdot f(x)}{x^2+1}\mathrm{\,d}x=2\). Tính \(I=\displaystyle\int\limits_{0}^{1}f(x)\mathrm{\,d}x\).
| \(6\) | |
| \(1\) | |
| \(0\) | |
| \(2\) |
Cho hàm số \(y=f(x)\) có đạo hàm liên tục trên \(\mathbb{R}\) và có một nguyên hàm là hàm số \(y=\dfrac{1}{2}x^2-x+1\). Giá trị của biểu thức \(\displaystyle\int\limits_1^2f\left(x^2\right)\mathrm{\,d}x\) bằng
| \(-\dfrac{4}{3}\) | |
| \(\dfrac{4}{3}\) | |
| \(-\dfrac{2}{3}\) | |
| \(\dfrac{2}{3}\) |
Cho hàm số $f(x)$ liên tục trên $\mathbb{R}$. Gọi $F(x)$ và $G(x)$ là hai nguyên hàm của $f(x)$ thỏa mãn $2F(3)+G(3)=9+2F(-1)+G(-1)$. Khi đó $\displaystyle\displaystyle\int\limits_0^2\big(x^2+f(3-2x)\big)\mathrm{\,d}x$ bằng
| $\dfrac{25}{6}$ | |
| $\dfrac{7}{6}$ | |
| $\dfrac{43}{6}$ | |
| $3$ |
Tính tích phân $\displaystyle\int\limits_{0}^{1}(2x+1)^5\mathrm{\,d}x$.
Cho hàm số trùng phương $f(x)=ax^4+bx^2+c$ có đồ thị như hình vẽ.
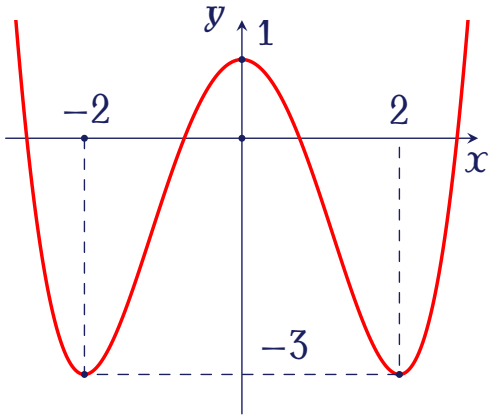
Hỏi đồ thị hàm số $y=\dfrac{2022}{\big[f(x)\big]^2+2f(x)-3}$ có tổng cộng bao nhiêu tiệm cận đứng?
| $4$ | |
| $3$ | |
| $5$ | |
| $2$ |
Cho hàm số $f(x)$, trong đó $f(x)$ là một đa giác. Hàm số $f'(x)$ có đồ thị như hình vẽ bên.
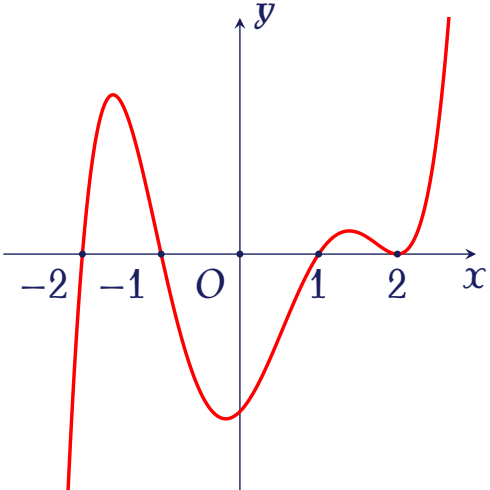
Hỏi có bao nhiêu giá trị nguyên $m$ thuộc $(-5;5)$ để hàm số $y=g(x)=f\big(x^2-2|x|+m\big)$ có $9$ điểm cực trị?
| $3$ | |
| $4$ | |
| $1$ | |
| $2$ |
Cho hàm số $y=f(x)$ có bảng xét dấu của $f'(x)$ như sau:
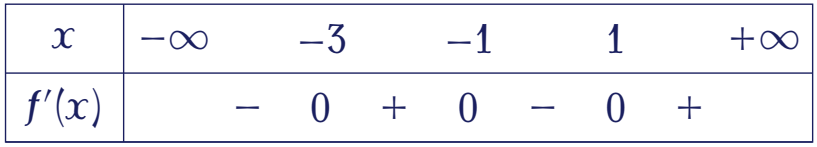
Hàm số $y=f(5-2x)$ đồng biến trên khoảng nào dưới đây?
| $(1;3)$ | |
| $(-\infty;-3)$ | |
| $(3;4)$ | |
| $(4;5)$ |
Cho hàm số bậc hai $y=f(x)$ có đồ thị như hình vẽ.
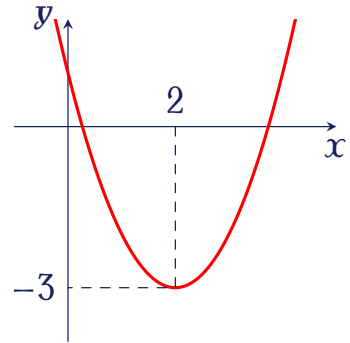
Tìm số nghiệm thực của phương trình $\big|f\big(x^3-2x^2+x\big)\big|=2$.
| $1$ | |
| $3$ | |
| $4$ | |
| $2$ |
Cho hàm số bậc ba $y=f(x)$ có đồ thị như hình vẽ.
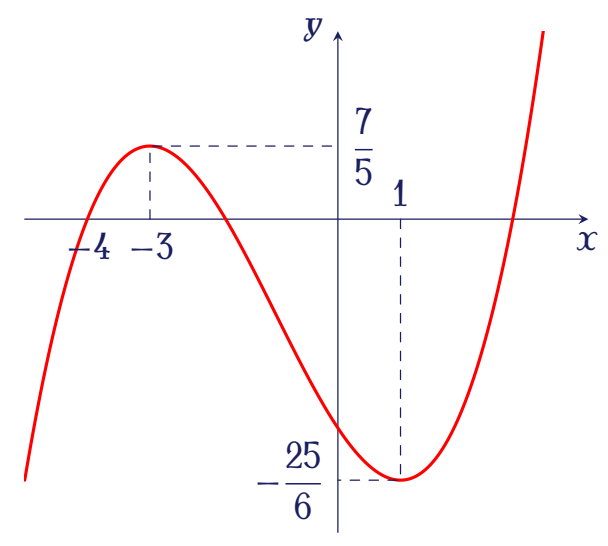
Tìm số nghiệm thực của phương trình $\big|f\big(x^2-4x\big)\big|=\dfrac{3}{4}$.
| $12$ | |
| $6$ | |
| $10$ | |
| $8$ |
Cho hàm số bậc ba $y=f(x)$ có đồ thị như hình vẽ.
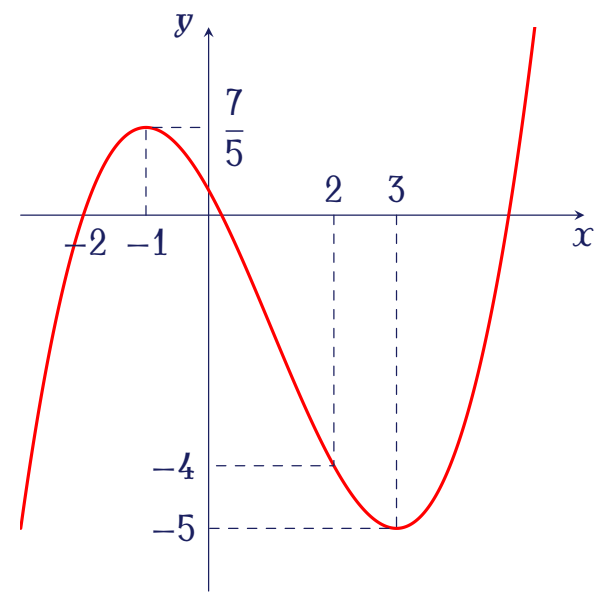
Tìm số nghiệm thực của phương trình $\big|f\big(x^3-3x\big)\big|=2$.
| $12$ | |
| $6$ | |
| $10$ | |
| $8$ |
Cho hàm số $y=f(x)$ có đạo hàm $f'(x)=(x-1)^2\big(x^2-2x\big)$ với $\forall x\in\mathbb{R}$. Có bao nhiêu giá trị nguyên dương của tham số $m$ để hàm số $f\big(x^2-8x+m\big)$ có $5$ điểm cực trị?
| $17$ | |
| $15$ | |
| $16$ | |
| $18$ |
