Tìm phần thực, phần ảo, số phức liên hợp và tính môđun của số phức $$z=\left(2-4i\right)\left(5+2i\right)+\dfrac{4-5i}{2+i}.$$
Cho hai số phức \(z_1=3+2i\) và \(z_2=1-5i\). Tìm phần thực và phần ảo của số phức \(z_1+z_2\).
| Phần thực là \(4\) và phần ảo là \(3\) | |
| Phần thực là \(4\) và phần ảo là \(-3i\) | |
| Phần thực là \(4\) và phần ảo là \(3i\) | |
| Phần thực là \(4\) và phần ảo là \(-3\) |
Cho số phức \(z=a+bi\). Số phức \(z^2\) có phần thực và phần ảo là
| \(a^2+b^2\) và \(2a^2b^2\) | |
| \(a+b\) và \(a^2b^2\) | |
| \(a^2-b^2\) và \(2ab\) | |
| \(a-b\) và \(ab\) |
Cho số phức \(z\) thỏa mãn $$(3+2\mathrm{i})z+(2-\mathrm{i})^2=4+\mathrm{i}$$Hiệu phần thực và phần ảo của \(z\) là
| \(2\) | |
| \(3\) | |
| \(1\) | |
| \(0\) |
Tổng phần thực và phần ảo của số phức \(z=(1+\mathrm{i})^2-(3+3\mathrm{i})\) bằng
| \(\sqrt{10}\) | |
| \(-4\) | |
| \(4\) | |
| \(-3-\mathrm{i}\) |
Tìm phần thực \(a\) và phần ảo \(b\) của số phức $$z=(-2+3\mathrm{i})(-9-10\mathrm{i})$$
| \(\begin{cases}a=48\\ b=7\end{cases}\) | |
| \(\begin{cases}a=-48\\ b=7\end{cases}\) | |
| \(\begin{cases}a=-48\\ b=-7\end{cases}\) | |
| \(\begin{cases}a=48\\ b=-7\end{cases}\) |
Cho hai số phức \(z_1=2+3\mathrm{i}\) và \(z_2=-3-5\mathrm{i}\). Tính tổng phần thực và phần ảo của số phức \(w=z_1+z_2\).
| \(-3\) | |
| \(0\) | |
| \(-1-2\mathrm{i}\) | |
| \(3\) |
Tìm phần thực và phần ảo của số phức $$z=2-\mathrm{i}+\left(\dfrac{1}{3}-2\mathrm{i}\right)$$
| \(\dfrac{7}{3}\) và \(-3\mathrm{i}\) | |
| \(\dfrac{7}{3}\) và \(-3\) | |
| \(\dfrac{7}{3}\) và \(2\) | |
| \(\dfrac{5}{3}\) và \(\dfrac{1}{2}\) |
Số phức \(z\) thỏa mãn điều kiện \((3+i)z+(1-2i)^2=8-17i\). Khi đó hiệu của phần thực và phần ảo của \(z\) là
| \(7\) | |
| \(-3\) | |
| \(3\) | |
| \(-7\) |
Cho hai số phức $z_1=2-i$ và $z_2=1+3i$. Phần thực của số phức $z_1-z_2$ bằng
| $3$ | |
| $-4$ | |
| $1$ | |
| $-1$ |
Điểm $M$ trong hình vẽ bên là điểm biểu diễn cho số phức $z$.
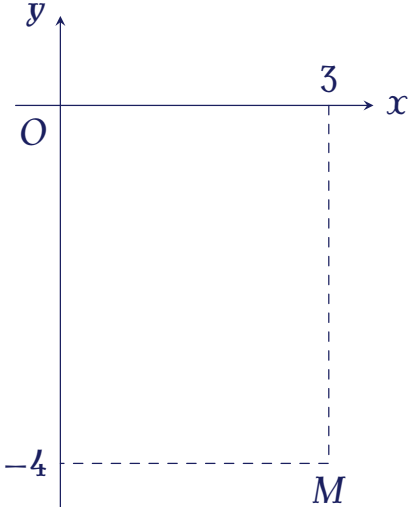
Phần ảo của số phức $(1+i)z$ bằng
| $7$ | |
| $-7$ | |
| $-1$ | |
| $1$ |
Cho số phức $z=1-3i$. Số phức $w=(1-i)z+\overline{z}$ có phần ảo bằng
| $1$ | |
| $-1$ | |
| $-i$ | |
| $i$ |
Cho số phức $z=2+9i$, phần thực của số phức $z^2$ bằng
| $-77$ | |
| $4$ | |
| $36$ | |
| $85$ |
Cho số phức $z$ thỏa mãn $(2-i)z=-3+7i$. Số phức liên hợp của $z$ có phần ảo bằng
| $-\dfrac{11}{5}$ | |
| $-\dfrac{11}{5}i$ | |
| $\dfrac{11}{5}i$ | |
| $\dfrac{11}{5}$ |
Cho hai số phức $z_1=3-2i$ và $z_2=\left(i+1\right)z_1$. Phần thực của số phức $w=2z_1-z_2$ bằng
| $1$ | |
| $-5$ | |
| $7$ | |
| $-1$ |
Số phức $z$ có điểm biểu diễn $M$ trong hình vẽ bên.
Phần ảo của số phức $z+i$ bằng
| $4$ | |
| $3i$ | |
| $2$ | |
| $6$ |
Điểm $A$ trong hình vẽ bên biểu diễn cho số phức $z$. Mệnh đề nào sau đây đúng?
| Phần thực là $-3$, phần ảo là $2$ | |
| Phần thực là $-3$, phần ảo là $2i$ | |
| Phần thực là $3$, phần ảo là $-2i$ | |
| Phần thực là $3$, phần ảo là $2$ |
Cho số phức $z$ thỏa mãn $(2-i)z+3i+2=0$. Phần thực của số phức $z$ bằng
| $-\dfrac{1}{5}$ | |
| $-\dfrac{8}{5}$ | |
| $\dfrac{8}{5}$ | |
| $\dfrac{1}{5}$ |
Cho số phức $z$ thỏa mãn $i\overline{z}=5+2i$. Phần ảo của $z$ bằng
| $5$ | |
| $2$ | |
| $-5$ | |
| $-2$ |
Biết phương trình $z^2+2z+m=0$ ($m\in\mathbb{R}$) có một nghiệm là $z_1=-1+3i$. Gọi $z_2$ là nghiệm còn lại. Phần ảo của số phức $w=z_1-2z_2$ bằng
| $1$ | |
| $-3$ | |
| $9$ | |
| $-9$ |
