Tìm phần thực, phần ảo, số phức liên hợp và tính môđun của số phức $$z=\left(2-4i\right)\left(5+2i\right)+\dfrac{4-5i}{2+i}.$$
Biết phương trình $z^2+2z+m=0$ ($m\in\mathbb{R}$) có một nghiệm là $z_1=-1+3i$. Gọi $z_2$ là nghiệm còn lại. Phần ảo của số phức $w=z_1-2z_2$ bằng
| $1$ | |
| $-3$ | |
| $9$ | |
| $-9$ |
Gọi $z_1$ và $z_2$ là hai nghiệm phức của phương trình $z^2-2z+5=0$, trong đó $z_2$ có phần ảo âm. Tìm phần ảo $b$ của số phức $w=\left[\left(z_1-i\right)\left(z_2+2i\right)\right]^{2018}$.
| $b=2^{1009}$ | |
| $b=2^{2017}$ | |
| $b=-2^{2018}$ | |
| $b=2^{2018}$ |
Gọi \(z_0\) là nghiệm phức có phần ảo dương của phương trình \(z^2+6z+13=0\). Trên mặt phẳng tọa độ, điểm biểu diễn số phức \(1-z_0\) là
| \(N\left(-2;2\right)\) | |
| \(M\left(4;2\right)\) | |
| \(P\left(4;-2\right)\) | |
| \(Q\left(2;-2\right)\) |
Cho hai số phức $z_1=3-i$ và $z_2=-2+5i$. Khi đó mô-đun của số phức $z=z_1+z_2$ bằng
| $\sqrt{17}$ | |
| $2\sqrt{17}$ | |
| $\sqrt{39}$ | |
| $\sqrt{10}$ |
Xét số phức $z$ thỏa mãn $|z+3-2i|+|z-3+i|=3\sqrt{5}$. Gọi $M,\,m$ lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức $P=|z+2|+|z-1-3i|$. Khi đó
| $M=\sqrt{26}+2\sqrt{5}$, $m=3\sqrt{2}$ | |
| $M=\sqrt{17}+\sqrt{5}$, $m=\sqrt{2}$ | |
| $M=\sqrt{26}+2\sqrt{5}$, $m=\sqrt{2}$ | |
| $M=\sqrt{17}+\sqrt{5}$, $m=3\sqrt{2}$ |
Cho số phức $z=a+bi$ ($a,\,b\in\mathbb{R}$) thỏa mãn $z-4=(1+i)|z|-(4+3z)i$. Giá trị của biểu thức $P=a-3b$ bằng
| $P=-2$ | |
| $P=6$ | |
| $P=2$ | |
| $P=-6$ |
Điểm $M$ trong hình vẽ bên là điểm biểu diễn cho số phức $z$.
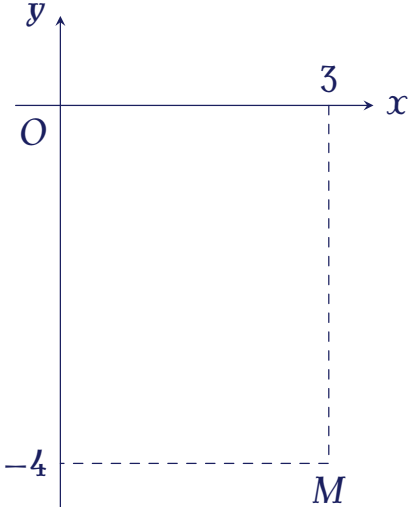
Phần ảo của số phức $(1+i)z$ bằng
| $7$ | |
| $-7$ | |
| $-1$ | |
| $1$ |
Cho số phức $z=1-3i$. Số phức $w=(1-i)z+\overline{z}$ có phần ảo bằng
| $1$ | |
| $-1$ | |
| $-i$ | |
| $i$ |
Cho số phức $z=a+bi$ ($a,\,b\in\mathbb{R}$) tùy ý. Mệnh đề nào sau đây đúng?
| Số phức liên hợp của $z$ có mô-đun bằng mô-đun của $iz$ | |
| $z^2=|z|^2$ | |
| Điểm $M(-a;b)$ là điểm biểu diễn của $\overline{z}$ | |
| Mô-đun của $z$ là một số thực dương |
Cho số phức $z$ thỏa mãn $z=\dfrac{\left(1+\sqrt{3}i\right)^3}{1-i}$. Tìm mô-đun của $iz$.
| $4$ | |
| $4\sqrt{2}$ | |
| $8\sqrt{2}$ | |
| $8$ |
Tên tập hợp số phức, xét phương trình $z^2-2(m+1)z+m^2=0$ ($m$ là tham số thực). Có bao nhiêu giá trị của $m$ để phương trình đó có hai nghiệm phân biệt $z_1$, $z_2$ thỏa mãn $\big|z_1\big|+\big|z_2\big|=2$?
| $1$ | |
| $4$ | |
| $2$ | |
| $3$ |
Có bao nhiêu số phức $z$ thỏa mãn $\big|z^2\big|=2\big|z-\overline{z}\big|$ và $\left|(z-4)\big(\overline{z}-4i\big)\right|=|z+4i|^2$?
| $3$ | |
| $1$ | |
| $2$ | |
| $4$ |
Cho các số phức $z_1,\,z_2,\,z_3$ thỏa mãn $\big|z_1\big|=\big|z_2\big|=2\big|z_3\big|=2$ và $8\big(z_1+z_2\big)z_3=3z_1z_2$. Gọi $A,\,B,\,C$ lần lượt là các điểm biểu diễn của $z_1,\,z_2,\,z_3$ trên mặt phẳng tọa độ. Diện tích tam giác $ABC$ bằng
| $\dfrac{\sqrt{55}}{32}$ | |
| $\dfrac{\sqrt{55}}{16}$ | |
| $\dfrac{\sqrt{55}}{24}$ | |
| $\dfrac{\sqrt{55}}{8}$ |
Cho số phức $z$ thỏa mãn $(2-i)z=-3+7i$. Số phức liên hợp của $z$ có phần ảo bằng
| $-\dfrac{11}{5}$ | |
| $-\dfrac{11}{5}i$ | |
| $\dfrac{11}{5}i$ | |
| $\dfrac{11}{5}$ |
Trên tập hợp các số phức, xét phương trình $z^2-2(m+1)z+m^2=0$ ($m$ là tham số thực). Có bao nhiêu giá trị của $m$ để phương trình đó có nghiệm $z_0$ thỏa mãn $\left|z_0\right|=7$?
| $2$ | |
| $3$ | |
| $1$ | |
| $4$ |
Gọi $z_0$ là nghiệm phức có phần ảo dương của phương trình $z^2+6z+13=0$. Tọa độ điểm biểu diễn của số phức $w=\left(1+i\right)z_0$ là
| $\left(5;1\right)$ | |
| $\left(-1;-5\right)$ | |
| $\left(1;5\right)$ | |
| $\left(-5;-1\right)$ |
Cho hai số phức $z_1=2+3i$ và $z_2=1-i$. Môđun của số phức $2z_1-3z_2$ bằng
| $\sqrt{58}$ | |
| $\sqrt{113}$ | |
| $\sqrt{82}$ | |
| $\sqrt{137}$ |
Cho số phức $z$ có phần thực là số nguyên và $z$ thỏa mãn $|z|-2\overline{z}=-7+3i+z$. Tính môđun của số phức $\omega=1-z$.
| $|\omega|=\sqrt{37}$ | |
| $|\omega|=3\sqrt{2}$ | |
| $|\omega|=7$ | |
| $|\omega|=5$ |
Số phức $z$ có điểm biểu diễn $M$ trong hình vẽ bên.
Phần ảo của số phức $z+i$ bằng
| $4$ | |
| $3i$ | |
| $2$ | |
| $6$ |
