Cho hàm số $f(x)=\dfrac{ax-1}{bx+c}\,(a,\,b,\,c\in\mathbb{R})$ có bảng biến thiên như hình bên.
Giá trị của $a-b-c$ thuộc khoảnh nào sau đây?
| $\left(-1;0\right)$ | |
| $\left(-2;-1\right)$ | |
| $\left(1;2\right)$ | |
| $\left(0;1\right)$ |
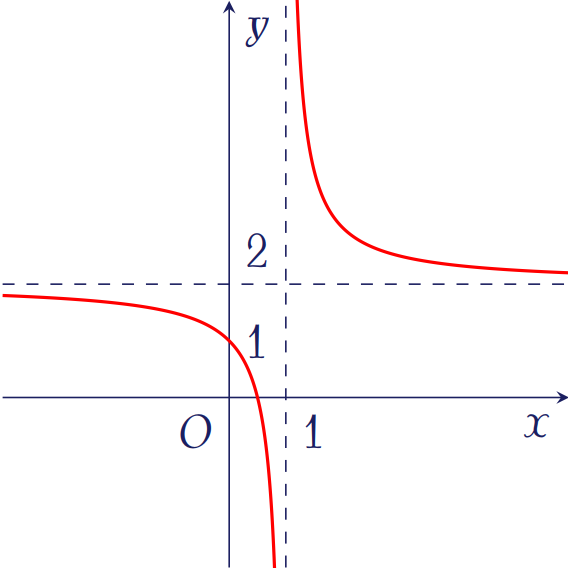
Cho hàm số \(y=\dfrac{ax-1}{bx+c}\) có đồ thị như hình trên. Tính giá trị biểu thức \(T=a+2b+3c\).
| \(T=1\) | |
| \(T=2\) | |
| \(T=3\) | |
| \(T=4\) |
Cho hàm số $y=\dfrac{ax+b}{cx+1}$ ($a,\,b,\,c\in\mathbb{R}$) có đồ thị như hình bên.
Khi đó $a+b-c$ bằng
| $-2$ | |
| $-1$ | |
| $1$ | |
| $0$ |
Cho hàm số $y=f(x)$ xác định trên $\mathbb{R}\setminus\{0\}$, liên tục trên mỗi khoảng xác định và có bảng biến thiên như hình bên.
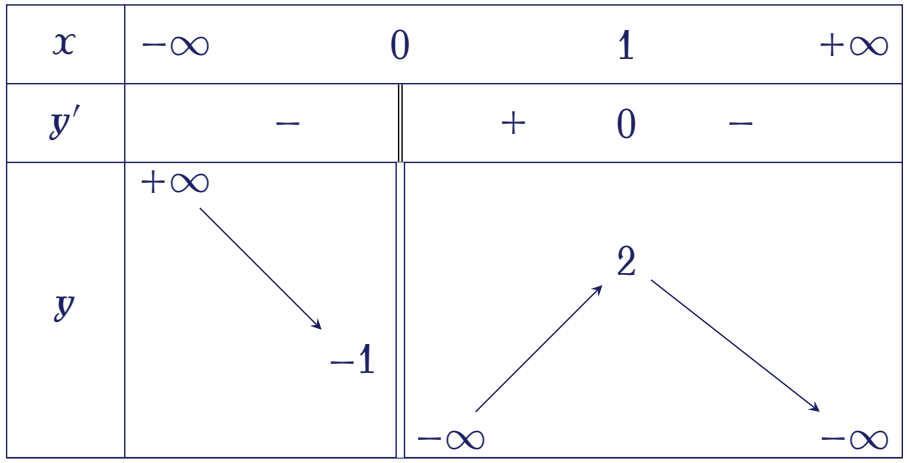
Tập hợp tất cả các giá trị của tham số $m$ sao cho phương trình $f(x)=m$ có ba nghiệm phân biệt là
| $(-\infty;2)$ | |
| $\{-1;2\}$ | |
| $[-1;2]$ | |
| $(-1;2)$ |
Bảng biến thiên trong hình bên là của hàm số nào trong các hàm số đã cho dưới đây?
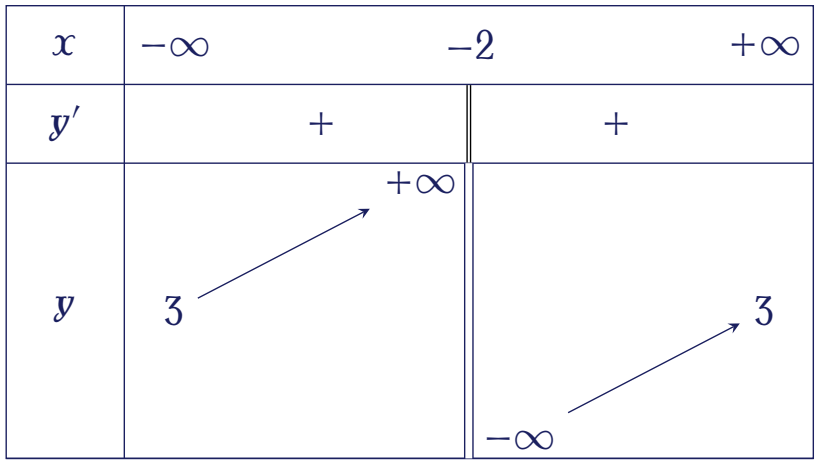
| $y=\dfrac{3-x}{x+2}$ | |
| $y=\dfrac{3x+8}{x+2}$ | |
| $y=\dfrac{3x-3}{x+2}$ | |
| $y=\dfrac{3-3x}{x+2}$ |
Cho hàm số $y=f(x)$ xác định trên $\mathbb{R}\setminus\{1\}$ và có bảng biến thiên như sau :
Mệnh đề nào sau đây đúng?
| Hàm số đồng biến trên khoảng $\left(2;+\infty\right)$ | |
| Hàm số nghịch biến trên khoảng $\left(-\infty;2\right)$ | |
| Hàm số nghịch biến trên các khoảng $\left(-\infty;1\right)$ và $\left(1;+\infty\right)$ | |
| Hàm số nghịch biến trên $\mathbb{R}$ |
Cho hàm số \(y=f(x)\) xác định, liên tục trên \(\mathbb{R}\) và có bảng biến thiên như sau:
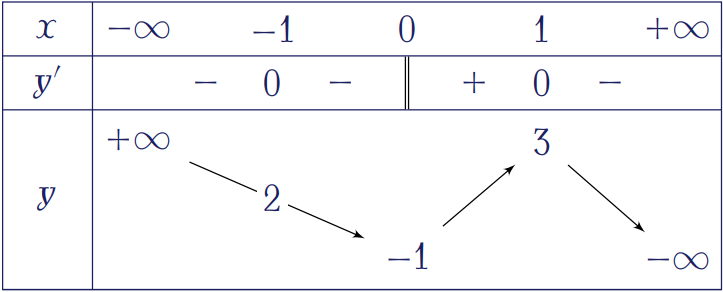
Có bao nhiêu giá trị nguyên của tham số \(m\) để phương trình \(f(x)-2-m=0\) có \(3\) nghiệm phân biệt?
| \(5\) | |
| \(4\) | |
| \(3\) | |
| \(2\) |
Cho hàm số \(y=f(x)\) xác định, liên tục trên \(\mathbb{R}\) và có bảng biến thiên như sau:
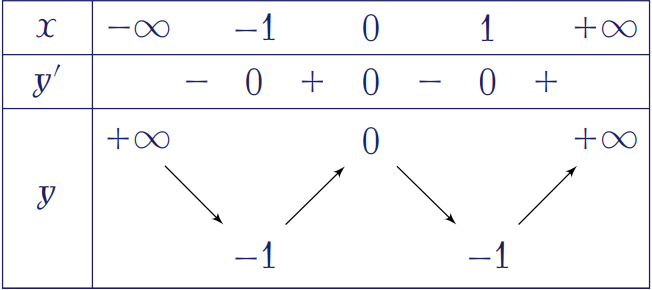
Tìm tất cả các giá trị thực của tham số \(m\) để phương trình \(f(x)-1=m\) có đúng \(2\) nghiệm.
| \(-2< m<-1\) | |
| \(m=-2\) hoặc \(m\geq-1\) | |
| \(m=-1\) hoặc \(m>0\) | |
| \(m=-2\) hoặc \(m>-1\) |
Cho hàm số \(y=f(x)\) xác định trên \(\mathbb{R}\setminus\{0\}\), liên tục trên từng khoảng xác định và có bảng biến thiên như hình.

Tìm tập hợp các giá trị thực của tham số \(m\) để phương trình \(f(x)=m\) có \(3\) nghiệm phân biệt.
| \([-2;2)\) | |
| \((-2;2)\) | |
| \((-2;2]\) | |
| \([2;+\infty)\) |
Cho hàm số \(y=f(x)\) xác định trên \(\mathbb{R}\setminus\{0\}\), liên tục trên từng khoảng xác định và có bảng biến thiên như hình.
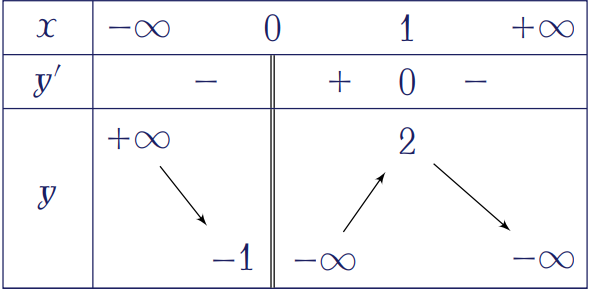
Phương trình \(f(x)=m\) với \(m\in(-1;2)\) có bao nhiêu nghiệm?
| \(3\) | |
| \(1\) | |
| \(0\) | |
| \(2\) |
Cho hàm số \(y=f(x)\) xác định, liên tục trên \(\mathbb{R}\) và có bảng biến thiên như sau:

Tìm tất cả các giá trị thực của tham số \(m\) để phương trình \(f(x)-m=0\) có \(3\) nghiệm phân biệt.
| \(-3\leq m\leq2\) | |
| \(-3< m<2\) | |
| \(-4\leq m\leq2\) | |
| \(-4< m<2\) |
Cho hàm số \(y=f(x)\) xác định, liên tục trên \(\mathbb{R}\) và có bảng biến thiên như sau:

Tập hợp các giá trị thực của tham số \(m\) để phương trình \(f(x)=m\) có đúng một nghiệm là
| \((-\infty;-2)\cup(2;+\infty)\) | |
| \((-\infty;-2]\cup[2;+\infty)\) | |
| \((-2;2)\) | |
| \([-2;2]\) |
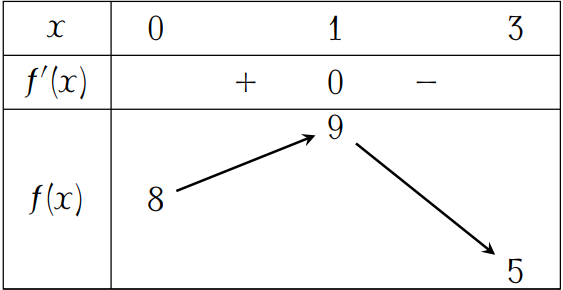
Cho hàm số \(y=f(x)\) có bảng biến thiên như hình. Gọi \(S\) là tập hợp các số nguyên dương \(m\) để bất phương trình $$f(x)\geq mx^2\left(x^2-2\right)+2m$$có nghiệm thuộc đoạn \([0;3]\). Số phần tử của tập \(S\) là
| \(9\) | |
| \(10\) | |
| Vô số | |
| \(0\) |
Cho hàm số $y=\dfrac{ax+b}{cx+d}$ có đồ thị là đường cong trong hình vẽ bên.
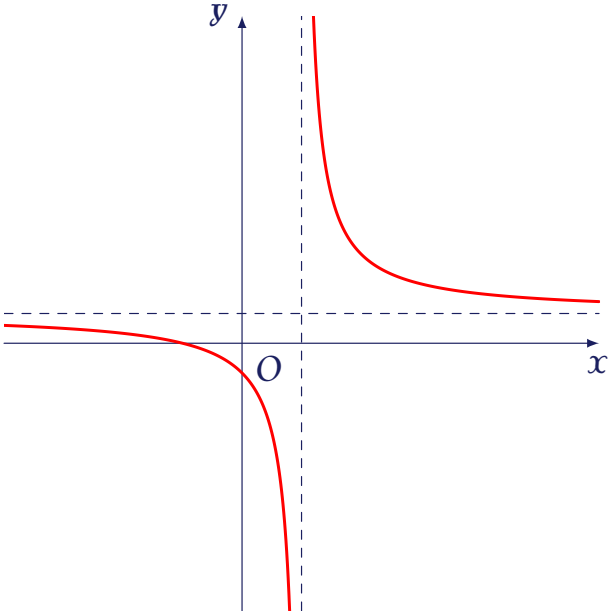
Kết luận nào sau đây đúng?
| $ad>0$, $bc< 0$ | |
| $ad< 0$, $bc>0$ | |
| $ad< 0$, $bc< 0$ | |
| $ad>0$, $bc>0$ |
Cho hàm số bậc bốn $y=f(x)$ có đồ thị là đường cong như hình vẽ bên dưới.
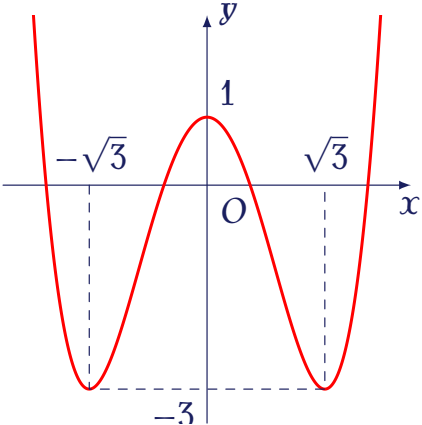
Có bao nhiêu giá trị nguyên âm của tham số $m$ để phương trình $f(x)=m$ có bốn nghiệm thực phân biệt?
| $3$ | |
| $2$ | |
| $4$ | |
| $5$ |
Hàm số nào dưới đây có bảng biến thiên như hình bên?
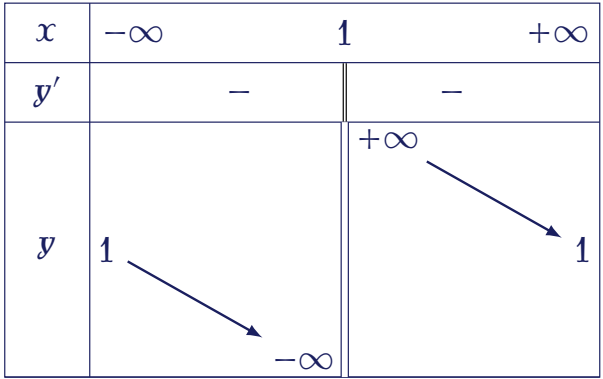
| $y=-x^3+3x+1$ | |
| $y=\dfrac{x-1}{x+1}$ | |
| $y=\dfrac{x+1}{x-1}$ | |
| $y=x^4-x^2+1$ |
Cho hàm số $y=f(x)$ liên tục và có bảng biến thiên trên đoạn $[-1;3]$ như hình vẽ.
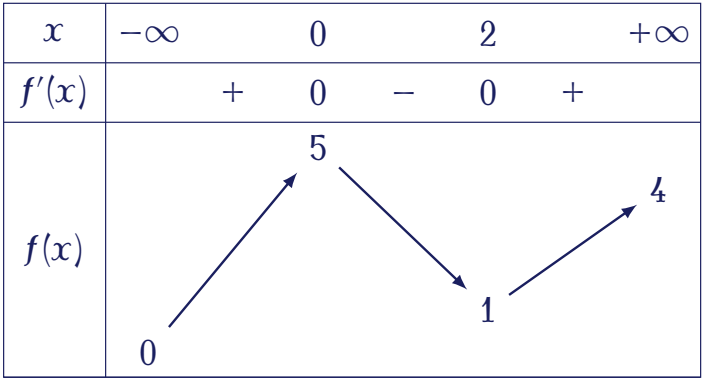
Khẳng định nào sau đây đúng?
| $\max\limits_{[-1;3]}f(x)=f(0)$ | |
| $\max\limits_{[-1;3]}f(x)=f(3)$ | |
| $\max\limits_{[-1;3]}f(x)=f(-1)$ | |
| $\max\limits_{[-1;3]}f(x)=f(2)$ |
Cho hàm số $y=f(x)$ có bảng biến thiên như sau:
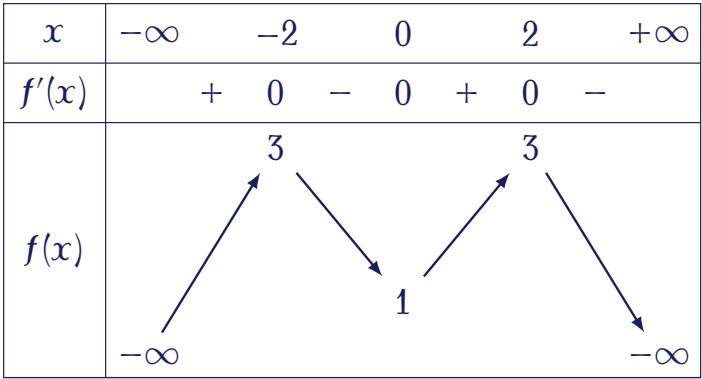
Số điểm cực tiểu của hàm số đã cho là
| $0$ | |
| $3$ | |
| $2$ | |
| $1$ |
Cho hàm số $y=f(x)$ có bảng biến thiên như hình vẽ dưới đây:
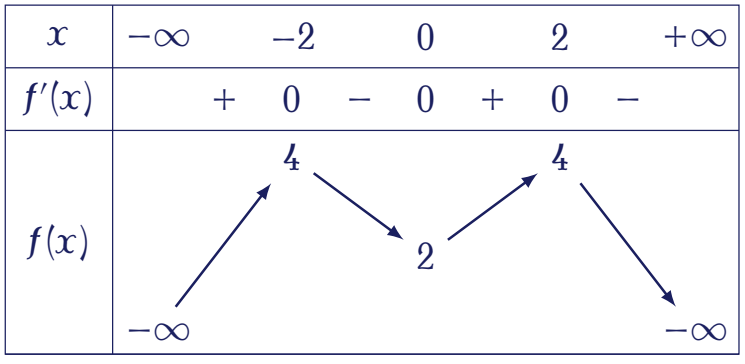
Số nghiệm của phương trình $f^2(x)-4f(x)+3=0$ là
| $5$ | |
| $3$ | |
| $6$ | |
| $4$ |
Cho hàm số $f(x)$ có bảng biến thiên như sau:
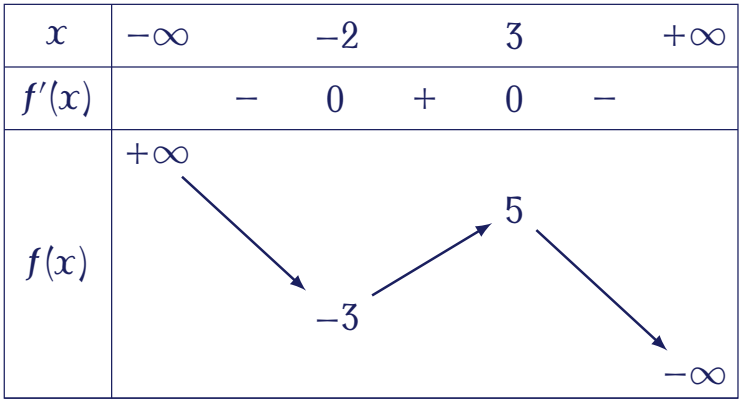
Hàm số đã cho đạt cực đại tại
| $x=-2$ | |
| $x=3$ | |
| $x=5$ | |
| $x=-3$ |
