Hàm số nào sau đây là hàm số chẵn?

	\(y=\cos x\)
	\(y=\sin x\)
	\(y=\tan x\)
	\(y=\cot x\)

Mệnh đề nào sau đây là sai?

	Đồ thị hàm số \(y=\left|\sin x\right|\) đối xứng qua gốc tọa độ \(O\)
	Đồ thị hàm số \(y=\cos x\) đối xứng qua trục \(Oy\)
	Đồ thị hàm số \(y=\left|\tan x\right|\) đối xứng qua trục \(Oy\)
	Đồ thị hàm số \(y=\tan x\) đối xứng qua gốc tọa độ \(O\)

Trong các hàm số sau, hàm số nào là hàm số chẵn?

	\(y=\sin x\)
	\(y=\cos x\)
	\(y=\tan x\)
	\(y=\cot x\)

Trong các hàm số sau, hàm số nào là hàm số chẵn?

	$y=\sin2x$
	$y=x\cos x$
	$y=\cos x\cdot\cot x$
	$y=\cot x\cdot\sin x$

Trong các hàm số sau, hàm số nào là hàm số chẵn?

	$y=\sin x$
	$y=\cos x$
	$y=\tan x$
	$y=\cot x$

Hàm số nào sau đây là hàm số lẻ?

	$y=\cos^3x$
	$y=\sin x+\cos^3x$
	$y=\sin x+\tan^3x$
	$\tan^2x$

Trong các hàm số sau đây, hàm số nào là hàm số chẵn?

	$y=\cos2x$
	$y=\cot2x$
	$y=\tan2x$
	$y=\sin2x$

Mệnh đề nào sau đây là sai?

	$(\cos x)^{\prime}=-\sin x$
	$(\sin x)^{\prime}=-\cos x$
	$(\cot x)^{\prime}=-\dfrac{1}{\sin^2x}$
	$(\tan x)^{\prime}=\dfrac{1}{\cos^2x}$

Cho hàm số $f(x)=\dfrac{1}{\cos^2x}$. Trong các khẳng định sau, khẳng định nào đúng?

	$\displaystyle\displaystyle\int f(x)\mathrm{\,d}x=\tan x+C$
	$\displaystyle\displaystyle\int f(x)\mathrm{\,d}x=\cot x+C$
	$\displaystyle\displaystyle\int f(x)\mathrm{\,d}x=-\cot x+C$
	$\displaystyle\displaystyle\int f(x)\mathrm{\,d}x=-\tan x+C$

Hàm số $y=\cot x$ có đạo hàm là

	$y'=-\dfrac{1}{\cos^2x}$
	$y'=-\dfrac{1}{\sin^2x}$
	$y'=\tan x$
	$y'=\dfrac{1}{\sin^2x}$

Hàm số $y=\cos x$ có đạo hàm là

	$y'=\sin x$
	$y'=\dfrac{1}{\sin x}$
	$y'=-\cos x$
	$y'=-\sin x$

Tính tích phân $I=\displaystyle\displaystyle\int\limits_{0}^{\pi}x^2\cos2x\mathrm{d}x$ bằng cách đặt $\begin{cases}u=x^2\\ \mathrm{d}v=\cos2x\mathrm{d}x\end{cases}$. Mệnh đề nào dưới đây đúng?

	$I=\dfrac{1}{2}x^2\sin2x\bigg|_{0}^{\pi}-\displaystyle\displaystyle\int\limits_{0}^{\pi}x\sin2x\mathrm{d}x$
	$I=\dfrac{1}{2}x^2\sin2x\bigg|_{0}^{\pi}-2\displaystyle\displaystyle\int\limits_{0}^{\pi}x\sin2x\mathrm{d}x$
	$I=\dfrac{1}{2}x^2\sin2x\bigg|_{0}^{\pi}+2\displaystyle\displaystyle\int\limits_{0}^{\pi}x\sin2x\mathrm{d}x$
	$I=\dfrac{1}{2}x^2\sin2x\bigg|_{0}^{\pi}+\displaystyle\displaystyle\int\limits_{0}^{\pi}x\sin2x\mathrm{d}x$

Nguyên hàm $\displaystyle\displaystyle\int\sin x\mathrm{d}x$ là

	$-\cos x+C$
	$\cos x+C$
	$\dfrac{1}{2}\cos2x+C$
	$-\cos2x+C$

Chọn mệnh đề đúng trong các mệnh đề sau:

	Đồ thị của hàm số chẵn nhận trục tung làm trục đối xứng
	Đồ thị của hàm số lẻ nhận trục tung làm trục đối xứng
	Đồ thị của hàm số lẻ nhận trục hoành làm trục đối xứng
	Đồ thị của hàm số chẵn nhận trục hoành làm trục đối xứng

Hàm số \(y=\sin x\cos^3x\) là

	Hàm số lẻ
	Hàm số chẵn
	Hàm số không chẵn
	Hàm số không lẻ

Cho hàm số \(y=\tan x\) có đồ thị như hình vẽ:

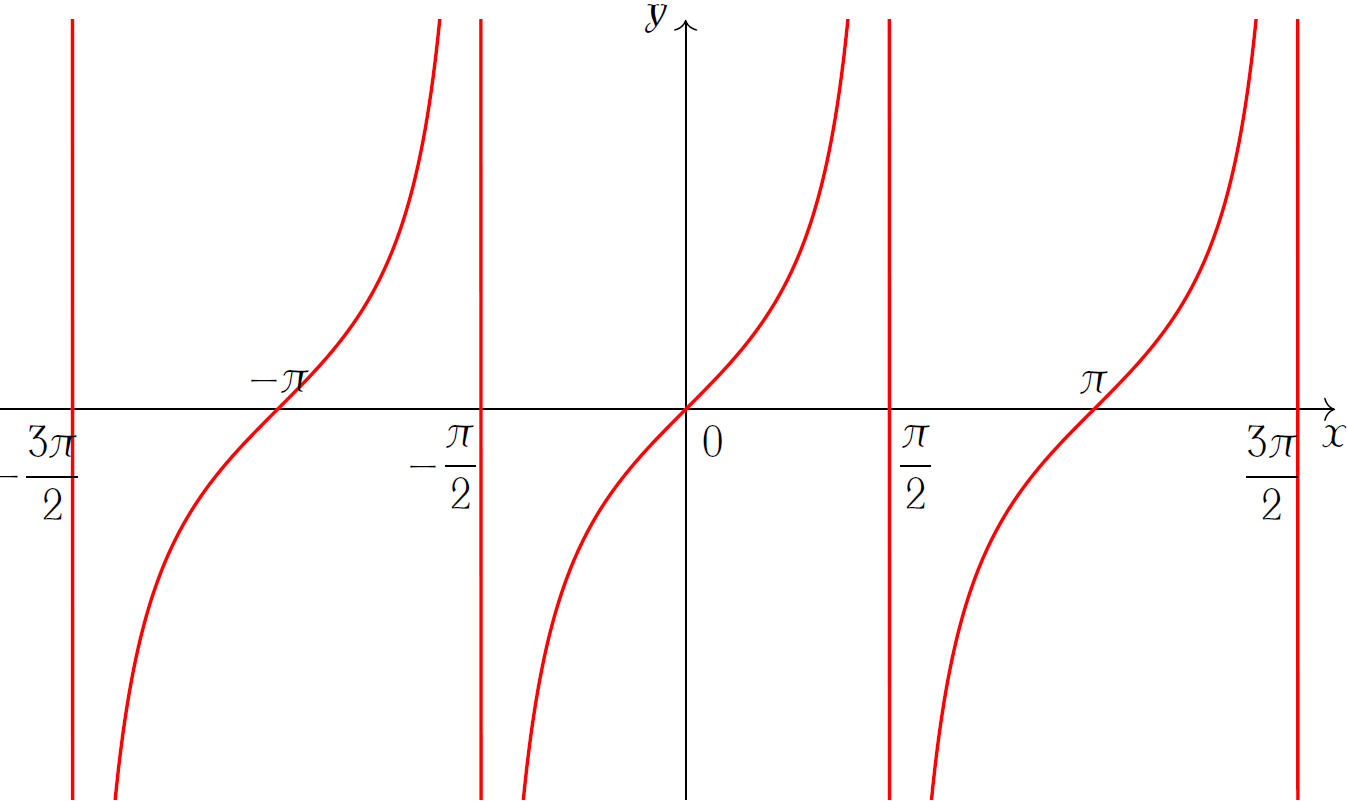
Khẳng định nào sau đây sai?

	Hàm số đồng biến trên \(\left(-\dfrac{\pi}{2};0\right)\)
	\(\tan x>0,\forall x\in\left(0;\dfrac{\pi}{2}\right)\)
	Đồ thị hàm số luôn cắt trục hoành tại một điểm
	Đồ thị hàm số nhận gốc tọa độ \(O\) làm tâm đối xứng nên hàm số \(y=\tan x\) là hàm số lẻ

Cho hai hàm số \(f(x)=\dfrac{\cos2x}{1+\sin^23x}\) và \(g(x)=\dfrac{\left|\sin2x\right|-\cos3x}{2+\tan^2x}\). Chọn mệnh đề đúng trong các mệnh đề sau:

	\(f(x)\) là hàm số chẵn, \(g(x)\) là hàm số lẻ
	\(f(x)\) là hàm số lẻ, \(g(x)\) là hàm số chẵn
	\(f(x)\) và \(g(x)\) đều là hàm số chẵn
	\(f(x)\) và \(g(x)\) đều là hàm số lẻ

Cho hai hàm số \(f(x)=\sin2x\) và \(g(x)=\tan^2x\). Chọn mệnh đề đúng trong các mệnh đề sau:

	\(f(x)\) là hàm số chẵn, \(g(x)\) là hàm số lẻ
	\(f(x)\) là hàm số lẻ, \(g(x)\) là hàm số chẵn
	\(f(x)\) và \(g(x)\) đều là hàm số chẵn
	\(f(x)\) và \(g(x)\) đều là hàm số lẻ

Hàm số nào sau đây có đồ thị đối xứng qua gốc tọa độ?

	\(y=\cot4x\)
	\(y=\dfrac{\sin x+1}{\cos x}\)
	\(y=\tan^2x\)
	\(y=\left|\cot x\right|\)

Trong các hàm số sau, hàm số nào là hàm số lẻ?

	\(y=\cos x+\sin^2x\)
	\(y=\sin x+\cos x\)
	\(y=-\cos x\)
	\(y=\sin x\cos3x\)