Hàm số \(y=\sin x\cos^3x\) là
| Hàm số lẻ | |
| Hàm số chẵn | |
| Hàm số không chẵn | |
| Hàm số không lẻ |
Cho hàm số \(y=\tan x\) có đồ thị như hình vẽ:
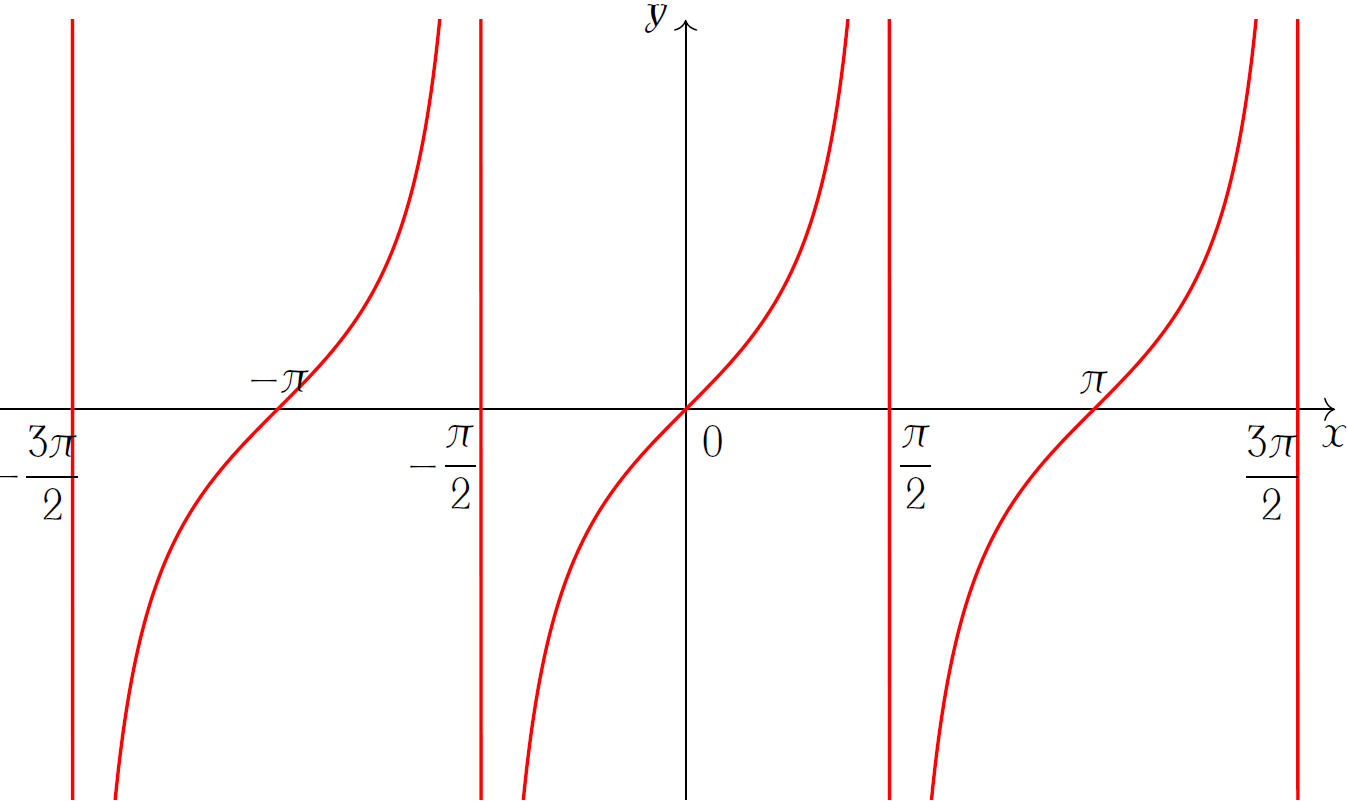
Khẳng định nào sau đây sai?
| Hàm số đồng biến trên \(\left(-\dfrac{\pi}{2};0\right)\) | |
| \(\tan x>0,\forall x\in\left(0;\dfrac{\pi}{2}\right)\) | |
| Đồ thị hàm số luôn cắt trục hoành tại một điểm | |
| Đồ thị hàm số nhận gốc tọa độ \(O\) làm tâm đối xứng nên hàm số \(y=\tan x\) là hàm số lẻ |
Trong các hàm số sau, hàm số nào là hàm số lẻ?
| \(y=\cos x+\sin^2x\) | |
| \(y=\sin x+\cos x\) | |
| \(y=-\cos x\) | |
| \(y=\sin x\cos3x\) |
Trong các hàm số sau, hàm số nào là hàm số chẵn?
| \(y=-\sin x\) | |
| \(y=\cos x-\sin x\) | |
| \(y=\cos x+\sin^2x\) | |
| \(y=\cos x\sin x\) |
Hàm số \(y=\sin^2x\cdot\left(1+\cos x\right)\) là hàm số
| chẵn | |
| lẻ | |
| không chẵn, không lẻ | |
| không có tính chẵn lẻ |
Tìm chu kỳ tuần hoàn \(\mathscr{T}\) của hàm số $$y=\sin\dfrac{x}{2}-\tan\left(2x+\dfrac{\pi}{4}\right).$$
| \(\mathscr{T}=4\pi\) | |
| \(\mathscr{T}=\pi\) | |
| \(\mathscr{T}=3\pi\) | |
| \(\mathscr{T}=2\pi\) |
Khẳng định nào sau đây sai?
| \(\displaystyle\int\dfrac{1}{\cos^2x}\mathrm{\,d}x=\tan x+C\) | |
| \(\displaystyle\int\dfrac{1}{\sin^2x}\mathrm{\,d}x=-\cot x+C\) | |
| \(\displaystyle\int\sin x\mathrm{\,d}x=\cos x+C\) | |
| \(\displaystyle\int\cos x\mathrm{\,d}x=\sin x+C\) |
Giá trị nhỏ nhất của hàm số $y=\dfrac{2\sin x+3}{\sin x+1}$ trên $\left[0;\dfrac{\pi}{2}\right]$ là
| $5$ | |
| $2$ | |
| $3$ | |
| $\dfrac{5}{2}$ |
Trong các hàm số sau, hàm số nào là hàm số chẵn?
| $y=\sin2x$ | |
| $y=x\cos x$ | |
| $y=\cos x\cdot\cot x$ | |
| $y=\cot x\cdot\sin x$ |
Trong các hàm số sau, hàm số nào là hàm số chẵn?
| $y=\sin x$ | |
| $y=\cos x$ | |
| $y=\tan x$ | |
| $y=\cot x$ |
Số giờ có ánh sáng mặt trời của một thành phố $X$ ở vĩ độ $40^{\circ}$ Bắc trong ngày thứ $t$ của năm 2015 được cho bởi hàm số $y=2\sin\left[\dfrac{\pi}{180}(t-70)\right]+13$ với $t\in\mathbb{Z}$ và $0< t\leq365$. Thành phố $X$ có đúng $11$ giờ có ánh sáng mặt trời vào ngày thứ bao nhiêu trong năm?
| $300$ | |
| $70$ | |
| $180$ | |
| $340$ |
Giá trị lớn nhất $M$, giá trị nhỏ nhất $m$ của hàm số $y=\sin^2x+2\sin x+5$ là
| $M=8;\,m=5$ | |
| $M=5;\,m=2$ | |
| $M=8;\,m=4$ | |
| $M=8;\,m=2$ |
Hàm số $y=\sin2x$ là hàm số tuần hoàn với chu kỳ là
| $3\pi$ | |
| $\dfrac{\pi}{2}$ | |
| $2\pi$ | |
| $\pi$ |
Tìm chu kì $T_{0}$ của hàm số $f(x)=\tan2x$.
| $T_{0}=\pi$ | |
| $T_{0}=\dfrac{\pi}{4}$ | |
| $T_{0}=2\pi$ | |
| $T_{0}=\dfrac{\pi}{2}$ |
Xác định chu kỳ của hàm số $y=\sin x$.
| $2\pi$ | |
| $\dfrac{3\pi}{2}$ | |
| $\dfrac{\pi}{2}$ | |
| $\pi$ |
Hàm số nào sau đây là hàm số lẻ?
| $y=\cos^3x$ | |
| $y=\sin x+\cos^3x$ | |
| $y=\sin x+\tan^3x$ | |
| $\tan^2x$ |
Trong các hàm số sau đây, hàm số nào là hàm số chẵn?
| $y=\cos2x$ | |
| $y=\cot2x$ | |
| $y=\tan2x$ | |
| $y=\sin2x$ |
Tập xác định của hàm số $y=\dfrac{2}{\sqrt{2-\sin x}}$ là
| $(2;+\infty)$ | |
| $\mathbb{R}\setminus\{2\}$ | |
| $\mathbb{R}$ | |
| $[2;+\infty)$ |
Cho hàm số $y=\sqrt{\dfrac{1-\cos x}{1-\sin x}}$. Tập xác định của hàm số là
| $\mathbb{R}\setminus\{\pi+k\pi,\,k\in\mathbb{Z}\}$ | |
| $\mathbb{R}\setminus\left\{\dfrac{\pi}{2}+k2\pi,\,k\in\mathbb{Z}\right\}$ | |
| $\{k2\pi,\,k\in\mathbb{Z}\}$ | |
| $\mathbb{R}\setminus\{k\pi,\,k\in\mathbb{Z}\}$ |
