Cho tam giác \(ABC\) có trọng tâm \(G\), điểm \(N\) được xác định bởi hệ thức \(\overrightarrow{CN}=\dfrac{1}{2}\overrightarrow{BC}\). Hãy biểu diễn vectơ \(\overrightarrow{AC}\) theo hai vectơ \(\overrightarrow{AG}\) và \(\overrightarrow{AN}\).
| \(\overrightarrow{AC}=\dfrac{3}{4}\overrightarrow{AG}+\dfrac{1}{2}\overrightarrow{AN}\) | |
| \(\overrightarrow{AC}=\dfrac{2}{3}\overrightarrow{AG}+\dfrac{1}{2}\overrightarrow{AN}\) | |
| \(\overrightarrow{AC}=\dfrac{4}{3}\overrightarrow{AG}-\dfrac{1}{2}\overrightarrow{AN}\) | |
| \(\overrightarrow{AC}=\dfrac{3}{4}\overrightarrow{AG}-\dfrac{1}{2}\overrightarrow{AN}\) |
Cho tam giác \(ABC\) có trọng tâm \(G\). Hãy phân tích vectơ \(\overrightarrow{AG}\) theo hai vectơ \(\overrightarrow{BA}\) và \(\overrightarrow{BC}\).
| \(\overrightarrow{AG}=\dfrac{2}{3}\overrightarrow{BA}+\dfrac{1}{3}\overrightarrow{BC}\) | |
| \(\overrightarrow{AG}=-\dfrac{2}{3}\overrightarrow{BA}+\dfrac{1}{3}\overrightarrow{BC}\) | |
| \(\overrightarrow{AG}=-\dfrac{2}{3}\overrightarrow{BA}-\dfrac{1}{3}\overrightarrow{BC}\) | |
| \(\overrightarrow{AG}=\dfrac{2}{3}\overrightarrow{BA}-\dfrac{1}{3}\overrightarrow{BC}\) |
Cho tam giác \(ABC\) đều cạnh \(a\). Tích vô hướng \(\overrightarrow{AB}\cdot\overrightarrow{AC}\) bằng
| \(2a\) | |
| \(\dfrac{a^2}{2}\) | |
| \(a^2\) | |
| \(-\dfrac{a^2}{2}\) |
Trong không gian, cho tứ diện $ABCD$ có trọng tâm $S$. Gọi $G$ là trọng tâm tam giác $BCD$, $M$ và $N$ lần lượt là trung điểm của $AB$, $CD$. Mệnh đề nào sau đây là sai?
| $S$ là trung điểm đoạn $MN$ | |
| $\overrightarrow{SA}+\overrightarrow{SB}+\overrightarrow{SC}+\overrightarrow{SD}=\overrightarrow{0}$ | |
| $S$ nằm trên đoạn $AG$ sao cho $SA=3SG$ | |
| $\overrightarrow{SA}+\overrightarrow{SB}+\overrightarrow{SC}+\overrightarrow{SD}=\overrightarrow{0}$ |
Trong không gian, điểm $S$ là trọng tâm của tam giác $ABC$ nếu
| $\overrightarrow{SA}+\overrightarrow{SB}+\overrightarrow{SC}=\overrightarrow{0}$ | |
| $\overrightarrow{SA}+\overrightarrow{SB}=\overrightarrow{SC}$ | |
| $\overrightarrow{SA}+\overrightarrow{SB}=\overrightarrow{0}$ | |
| $\overrightarrow{AB}+\overrightarrow{AC}=\overrightarrow{AS}$ |
Cho tứ diện $ABCD$ có $G$ là trọng tâm tam giác $BCD$. Mệnh đề nào sau đây không đúng?
| $\overrightarrow{AB}+\overrightarrow{AC}+\overrightarrow{AD}=3\overrightarrow{AG}$ | |
| $\overrightarrow{GB}+\overrightarrow{GC}+\overrightarrow{GD}=\overrightarrow{0}$ | |
| $\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}$ | |
| $\overrightarrow{AB}+\overrightarrow{AC}+\overrightarrow{AD}-3\overrightarrow{AG}=\overrightarrow{0}$ |
Trong không gian \(Oxyz\) cho điểm \(H(1;2;3)\). Viết phương trình mặt phẳng \((P)\) đi qua điểm \(H\) và cắt các trục tọa độ tại ba điểm phân biệt \(A,\,B,\,C\) sao cho \(H\) là trực tâm của tam giác \(ABC\).
| \((P)\colon x+\dfrac{y}{2}+\dfrac{z}{3}=1\) | |
| \((P)\colon x+2y+3z-14=0\) | |
| \((P)\colon x+y+z-6=0\) | |
| \((P)\colon\dfrac{x}{3}+\dfrac{y}{6}+\dfrac{z}{9}=1\) |
Trong mặt phẳng \(Oxy\), cho bốn điểm \(A(1;1)\), \(B(2;-1)\), \(C(4;3)\), \(D(3;5)\). Khẳng định nào sau đây đúng?
| Tứ giác \(ABCD\) là hình bình hành | |
| \(G(9;7)\) là trọng tâm tam giác \(BCD\) | |
| \(\overrightarrow{AB}=\overrightarrow{CD}\) | |
| \(\overrightarrow{AC},\,\overrightarrow{AD}\) cùng phương |
Cho tam giác \(ABC\) và điểm \(M\) thỏa mãn \(\overrightarrow{MA}=\overrightarrow{MB}+\overrightarrow{MC}\). Khẳng định nào sau đây đúng?
| \(A,\,B,\,C\) thẳng hàng | |
| \(AM\) là phân giác trong của góc \(\widehat{BAC}\) | |
| \(A,\,M\) và trọng tâm tam giác \(ABC\) thẳng hàng | |
| \(\overrightarrow{AM}+\overrightarrow{BC}=\vec{0}\) |
Cho tam giác \(ABC\). Có bao nhiêu điểm \(M\) thỏa mãn \(\left|\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}\right|=1\)?
| \(1\) | |
| \(2\) | |
| \(0\) | |
| Vô số |
Cho tam giác \(ABC\). Gọi \(M\) là điểm trên cạnh \(BC\) sao cho \(MB=3MC\). Hãy phân tích vectơ \(AM\) theo hai vectơ \(\overrightarrow{AB}\) và \(\overrightarrow{AC}\).
| \(\overrightarrow{AM}=-\dfrac{1}{4}\overrightarrow{AB}+\dfrac{3}{4}\overrightarrow{AC}\) | |
| \(\overrightarrow{AM}=\dfrac{1}{4}\overrightarrow{AB}+\dfrac{3}{4}\overrightarrow{AC}\) | |
| \(\overrightarrow{AM}=-\dfrac{1}{4}\overrightarrow{AB}-\dfrac{3}{4}\overrightarrow{AC}\) | |
| \(\overrightarrow{AM}=\dfrac{1}{4}\overrightarrow{AB}-\dfrac{3}{4}\overrightarrow{AC}\) |
Cho tam giác \(ABC\) đều, cạnh \(a\), có \(I,\,J,\,K\) lần lượt là trung điểm các cạnh \(BC,\,CA,\,AB\). Tính giá trị của $$\left|\overrightarrow{AI}+\overrightarrow{BJ}+\overrightarrow{CK}\right|.$$
| \(3a\) | |
| \(\dfrac{3a\sqrt{3}}{2}\) | |
| \(0\) | |
| \(\dfrac{a\sqrt{3}}{2}\) |
Biết \(G\) là trọng tâm tam giác \(ABC\). Mệnh đề nào sau đây đúng?
| \(\overrightarrow{AG}+\overrightarrow{BG}=\overrightarrow{CG}\) | |
| \(\overrightarrow{GA}+\overrightarrow{GB}=\overrightarrow{CG}\) | |
| \(\overrightarrow{GA}-\overrightarrow{GB}=\overrightarrow{CG}\) | |
| \(\overrightarrow{GA}-\overrightarrow{GB}=\overrightarrow{GC}\) |
Cho tam giác \(ABC\) có trọng tâm \(G\), \(M\) là trung điểm cạnh \(BC\). Mệnh đề nào sau đây sai?
| \(\overrightarrow{MB}+\overrightarrow{MC}=\vec{0}\) | |
| \(\overrightarrow{AB}+\overrightarrow{AC}=2\overrightarrow{AM}\) | |
| \(\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\vec{0}\) | |
| \(\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}=-3\overrightarrow{MG}\) |
Cho tam giác \(ABC\) có \(G\) là trọng tâm. Mệnh đề nào sau đây sai?
| \(\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}=3\overrightarrow{MG}\) | |
| \(\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\vec{0}\) | |
| \(\overrightarrow{GB}+\overrightarrow{GC}=2\overrightarrow{GA}\) | |
| \(3\overrightarrow{AG}=\overrightarrow{AB}+\overrightarrow{AC}\) |
Cho tam giác \(ABC\) có \(G\) là trọng tâm và \(I\) là trung điểm cạnh \(BC\). Đẳng thức nào sau đây đúng?
| \(\overrightarrow{GA}=2\overrightarrow{GI}\) | |
| \(\overrightarrow{IG}=-\dfrac{1}{3}\overrightarrow{IA}\) | |
| \(\overrightarrow{GB}+\overrightarrow{GC}=2\overrightarrow{GI}\) | |
| \(\overrightarrow{GB}+\overrightarrow{GC}=2\overrightarrow{GA}\) |
Cho tam giác \(ABC\) có \(M\) là trung điểm của \(BC\), \(G\) là trọng tâm. Khẳng định nào sau đây đúng?
| \(\overrightarrow{AG}=\dfrac{2}{3}\left(\overrightarrow{AB}+\overrightarrow{AC}\right)\) | |
| \(\overrightarrow{AG}=\dfrac{1}{3}\left(\overrightarrow{AB}+\overrightarrow{AC}\right)\) | |
| \(\overrightarrow{AG}=\dfrac{1}{3}\overrightarrow{AB}+\dfrac{2}{3}\overrightarrow{AC}\) | |
| \(\overrightarrow{AG}=\dfrac{2}{3}\overrightarrow{AB}+3\dfrac{1}{2}\overrightarrow{AC}\) |
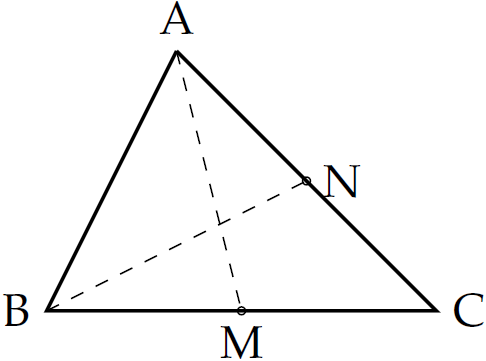
Bạn Thùy đặt một tấm bìa cứng hình tam giác (như hình vẽ) lên đầu một ngòi bút nhưng tấm bìa không bị rơi. Hỏi bạn Thùy đã đặt ngòi bút tại điểm nào của tấm bìa?
| Điểm \(A\) | |
| Trung điểm \(M\) | |
| Trung điểm \(N\) | |
| Giao điểm \(AM\) và \(BN\) |
Cho tam giác \(ABC\) đều, cạnh \(a\). Tính \(\left|\overrightarrow{AB}+\overrightarrow{AC}\right|\).
| \(\left|\overrightarrow{AB}+\overrightarrow{AC}\right|=2a\) | |
| \(\left|\overrightarrow{AB}+\overrightarrow{AC}\right|=a\sqrt{3}\) | |
| \(\left|\overrightarrow{AB}+\overrightarrow{AC}\right|=\dfrac{\sqrt{3}}{2}\) | |
| \(\left|\overrightarrow{AB}+\overrightarrow{AC}\right|=a\) |
Cho tam giác \(ABC\) đều, cạnh \(a\). Tính \(\left|\overrightarrow{AB}+\overrightarrow{BC}\right|\).
| \(\left|\overrightarrow{AB}+\overrightarrow{BC}\right|=2a\) | |
| \(\left|\overrightarrow{AB}+\overrightarrow{BC}\right|=a\sqrt{3}\) | |
| \(\left|\overrightarrow{AB}+\overrightarrow{BC}\right|=\dfrac{\sqrt{3}}{2}\) | |
| \(\left|\overrightarrow{AB}+\overrightarrow{BC}\right|=a\) |
