Tìm điều kiện xác định của hàm số $y=\tan2x$.

	$x\neq\dfrac{\pi}{8}+k\dfrac{\pi}{2}$, $k\in\mathbb{Z}$
	$x\neq\dfrac{\pi}{4}+k\pi$, $k\in\mathbb{Z}$
	$x\neq\dfrac{\pi}{2}+k\pi$, $k\in\mathbb{Z}$
	$x\neq\dfrac{\pi}{4}+k\dfrac{\pi}{2}$, $k\in\mathbb{Z}$

Tập xác định của hàm số \(y=\tan x\) là

	\(\mathscr{D}=\mathbb{R}\setminus\left\{\dfrac{\pi}{2}+k2\pi\,k\in\mathbb{Z}\right\}\)
	\(\mathscr{D}=\mathbb{R}\)
	\(\mathscr{D}=\mathbb{R}\setminus\left\{\dfrac{\pi}{2}+k\pi\,k\in\mathbb{Z}\right\}\)
	\(\mathscr{D}=\mathbb{R}\setminus\left\{k\pi\,k\in\mathbb{Z}\right\}\)

Tìm tập xác định \(\mathscr{D}\) của hàm số \(y=\tan x\).

	\(\mathscr{D}=\mathbb{R}\)
	\(\mathscr{D}=\mathbb{R}\setminus\{0\}\)
	\(\mathscr{D}=\mathbb{R}\setminus\left\{k\pi,\,k\in\mathbb{Z}\right\}\)
	\(\mathscr{D}=\mathbb{R}\setminus\left\{\dfrac{\pi}{2}+k\pi,\,k\in\mathbb{Z}\right\}\)

Hàm số \(y=\tan x\) xác định khi

	\(x\neq k2\pi\)
	\(x\neq\dfrac{\pi}{2}+k2\pi\)
	\(x\neq\dfrac{\pi}{2}+k\pi\)
	\(x\neq k\pi\)

Tìm tập xác định của hàm số $y=\cot\left(x+\dfrac{\pi}{3}\right)$.

Tìm tập xác định của hàm số $y=\cot\dfrac{x}{2}$.

	$\mathbb{R}\setminus\left\{k\pi,\,\,k\in\mathbb{Z}\right\}$
	$\mathbb{R}\setminus\left\{\dfrac{\pi}{2}+k\pi,\,\,k\in\mathbb{Z}\right\}$
	$\mathbb{R}\setminus\left\{k2\pi,\,k\in\mathbb{Z}\right\}$
	$\mathbb{R}\setminus\left\{\pi+k2\pi,\,k\in\mathbb{Z}\right\}$

Tập xác định của hàm số $y=\cos x$ là tập hợp nào trong các tập hợp dưới đây?

	$\mathbb{R}$
	$\mathbb{R}\setminus\left\{\dfrac{\pi}{2}+k2\pi,\,\,k\in\mathbb{Z}\right\}$
	$\mathbb{R}\setminus\left\{k\pi,\,\,k\in\mathbb{Z}\right\}$
	$\mathbb{R}\setminus\left\{\dfrac{\pi}{2}+k\pi,\,\,k\in\mathbb{Z}\right\}$

Tìm chu kì $T_{0}$ của hàm số $f(x)=\tan2x$.

	$T_{0}=\pi$
	$T_{0}=\dfrac{\pi}{4}$
	$T_{0}=2\pi$
	$T_{0}=\dfrac{\pi}{2}$

Tập xác định của hàm số $y=\dfrac{2}{\sqrt{2-\sin x}}$ là

	$(2;+\infty)$
	$\mathbb{R}\setminus\{2\}$
	$\mathbb{R}$
	$[2;+\infty)$

Cho hàm số $y=\sqrt{\dfrac{1-\cos x}{1-\sin x}}$. Tập xác định của hàm số là

	$\mathbb{R}\setminus\{\pi+k\pi,\,k\in\mathbb{Z}\}$
	$\mathbb{R}\setminus\left\{\dfrac{\pi}{2}+k2\pi,\,k\in\mathbb{Z}\right\}$
	$\{k2\pi,\,k\in\mathbb{Z}\}$
	$\mathbb{R}\setminus\{k\pi,\,k\in\mathbb{Z}\}$

Tập xác định của hàm số $y=\sin\dfrac{x}{x+1}$ là

	$\mathscr{D}=(-\infty;-1)\cup(0;+\infty)$
	$\mathscr{D}=(-1;+\infty)$
	$\mathscr{D}=\mathbb{R}$
	$\mathscr{D}=\mathbb{R}\setminus\{-1\}$

Điều kiện xác định của hàm số $y=\dfrac{2}{\cos x-1}$ là

	$\cos x\neq-1$
	$\cos x\neq1$
	$\cos x\neq2$
	$\cos x\neq0$

Đạo hàm của hàm số $y=\tan\left(2x+1\right)$ là

	$\dfrac{2}{\cos^2\left(2x+1\right)}$
	$-\dfrac{2}{\cos^2\left(2x+1\right)}$
	$\dfrac{1}{\cos^2\left(2x+1\right)}$
	$\dfrac{2}{\sin^2\left(2x+1\right)}$

Tìm đạo hàm của hàm số $y=\tan\left(\dfrac{\pi}{4}-x\right)$.

	$y'=-\dfrac{1}{\cos^2\left(\dfrac{\pi}{4}-x\right)}$
	$y'=\dfrac{1}{\cos^2\left(\dfrac{\pi}{4}-x\right)}$
	$y'=\dfrac{1}{\sin^2\left(\dfrac{\pi}{4}-x\right)}$
	$y'=-\dfrac{1}{\sin^2\left(\dfrac{\pi}{4}-x\right)}$

Tập xác định của hàm số \(y=\dfrac{\cot x}{\sin x-1}\) là

	\(\mathscr{D}=\mathbb{R}\setminus\left\{k\dfrac{\pi}{2}\bigg|k\in\mathbb{Z}\right\}\)
	\(\mathscr{D}=\mathbb{R}\setminus\left\{\dfrac{\pi}{3}+k2\pi\bigg|k\in\mathbb{Z}\right\}\)
	\(\mathscr{D}=\mathbb{R}\setminus\left\{\dfrac{\pi}{2}+k2\pi\bigg|k\in\mathbb{Z}\right\}\)
	\(\mathscr{D}=\mathbb{R}\setminus\left\{\dfrac{\pi}{2}+k2\pi;\,k\pi\bigg|k\in\mathbb{Z}\right\}\)

Cho hàm số \(y=\tan x\) có đồ thị như hình vẽ:

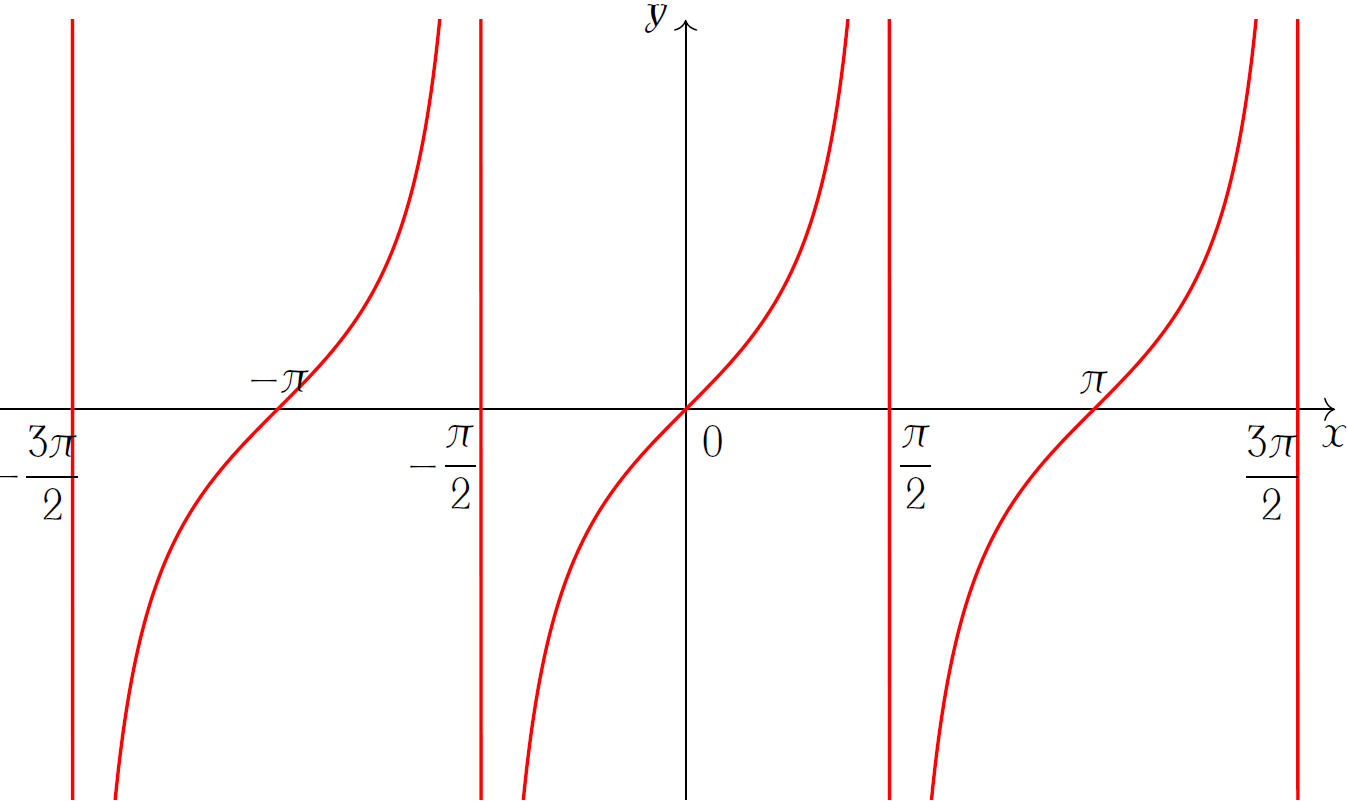
Khẳng định nào sau đây sai?

	Hàm số đồng biến trên \(\left(-\dfrac{\pi}{2};0\right)\)
	\(\tan x>0,\forall x\in\left(0;\dfrac{\pi}{2}\right)\)
	Đồ thị hàm số luôn cắt trục hoành tại một điểm
	Đồ thị hàm số nhận gốc tọa độ \(O\) làm tâm đối xứng nên hàm số \(y=\tan x\) là hàm số lẻ

Chu kì của hàm số \(f\left(x\right)=\tan\dfrac{x}{2}\) là

	\(T=4\pi\)
	\(T=\dfrac{\pi}{2}\)
	\(T=\pi\)
	\(T=2\pi\)

Hàm số nào sau đây có tập xác định là \(\mathscr{D}=\mathbb{R}\setminus\left\{k\pi,\,k\in\mathbb{Z}\right\}\)?

	\(y=\cot x\)
	\(y=\tan x\)
	\(y=\dfrac{1}{\sin x-1}\)
	\(y=\cos x\)

Hàm số nào sau đây có tập xác định là \(\mathbb{R}\)?

	\(y=\tan x+\sin\dfrac{7\pi}{12}\)
	\(y=\dfrac{1}{\sqrt{1-\cos x}}\)
	\(y=\cot2x\)
	\(y=\sqrt{1+\sin x}+\tan\dfrac{\pi}{12}\)

Tìm tập xác định \(\mathscr{D}\) của hàm số $$y=\sqrt{1-\sin2x}-\sqrt{1+\sin2x}$$

	\(\mathscr{D}=\mathbb{R}\)
	\(\mathscr{D}=\left[\dfrac{\pi}{6}+k2\pi;\dfrac{5\pi}{6}+k2\pi\right],\,k\in\mathbb{Z}\)
	\(\mathscr{D}=\left[\dfrac{5\pi}{6}+k2\pi;\dfrac{13\pi}{6}+k2\pi\right],\,k\in\mathbb{Z}\)
	\(\mathscr{D}=\varnothing\)