Tập hợp các giá trị \(m\) để đồ thị hàm số \(y=\dfrac{mx^2+6x-2}{x+2}\) có tiệm cận đứng là
| \(\left\{\dfrac{7}{2}\right\}\) | |
| \(\mathbb{R}\setminus\left\{-\dfrac{7}{2}\right\}\) | |
| \(\mathbb{R}\) | |
| \(\mathbb{R}\setminus\left\{\dfrac{7}{2}\right\}\) |
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số \(y=\dfrac{5x^2-4x-1}{x^2-1}\) là
| \(1\) | |
| \(0\) | |
| \(2\) | |
| \(3\) |
Cho hàm số \(y=\log_2x\). Khẳng định nào sau đây sai?
| Đồ thị hàm số nhận trục tung làm tiệm cận đứng | |
| Đồ thị hàm số cắt trục hoành tại điểm \(A(1;0)\) | |
| Đồ thị hàm số luôn nằm phía trên trục hoành | |
| Hàm số đồng biến trên khoảng \((0;+\infty)\) |
Cho hàm số \(y=\log_{2019}x\) có đồ thị \((\mathscr{C})\). Mệnh đề nào sau đây sai?
| \((\mathscr{C})\) có đúng một tiệm cận | |
| \((\mathscr{C})\) không có tiệm cận ngang | |
| \((\mathscr{C})\) đồng biến trên tập xác định | |
| \((\mathscr{C})\) không có tiệm cận đứng |
Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số $y=\dfrac{x-1}{x^2-2x-3}$ là
| $4$ | |
| $3$ | |
| $2$ | |
| $1$ |
Tiệm cận đứng của đồ thị hàm số $y=\dfrac{3x-2}{x+4}$ là đường thẳng có phương trình
| $x=4$ | |
| $x=3$ | |
| $x=-3$ | |
| $x=-4$ |
Cho hàm số $y=\dfrac{ax+b}{cx+1}$ ($a,\,b,\,c\in\mathbb{R}$) có đồ thị như hình bên.
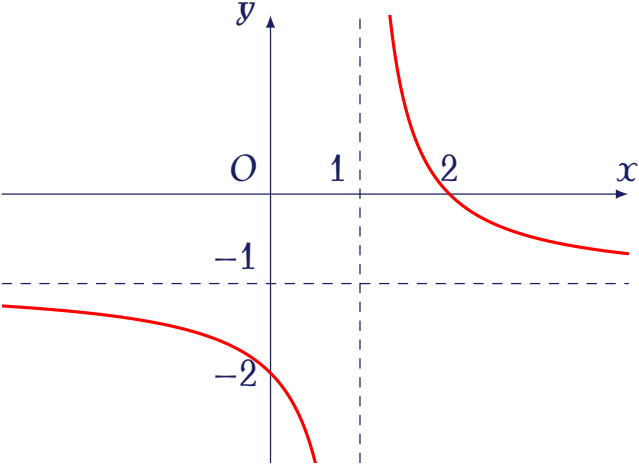
Khi đó $a+b-c$ bằng
| $-2$ | |
| $-1$ | |
| $1$ | |
| $0$ |
Cho hàm số $y=f(x)$ có bảng biến thiên như sau:
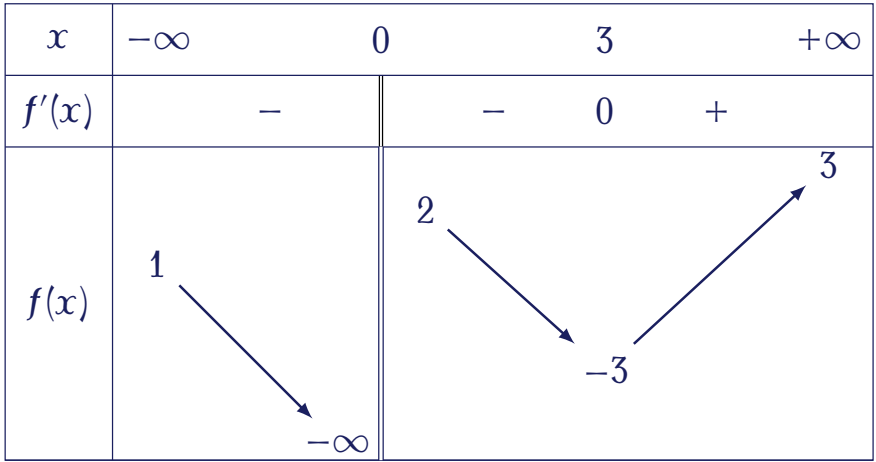
Tiệm cận đứng của đồ thị hàm số đã cho là
| $x=3$ | |
| $x=2$ | |
| $x=0$ | |
| $x=1$ |
Tiệm cận đứng của đồ thị hàm số $y=\dfrac{3x-1}{x-2}$ có phương trình là
| $x=2$ | |
| $x=-2$ | |
| $x=3$ | |
| $x=\dfrac{1}{2}$ |
Tiệm cận đứng của đồ thị hàm số $y=\dfrac{2x-1}{x+1}$ là đường thẳng có phương trình
| $y=-1$ | |
| $x=-1$ | |
| $y=2$ | |
| $x=2$ |
Tiệm cận ngang của đồ thị hàm số $y=3^x$ và tiệm cận đứng của đồ thị hàm số $y=\log_2x$ lần lượt có phương trình là
| $y=3$ và $x=0$ | |
| $x=0$ và $y=0$ | |
| $y=0$ và $x=2$ | |
| $y=0$ và $x=0$ |
Cho $\lim\limits_{x\to x_0^+}f(x)=5$, $\lim\limits_{x\to x_0^-}f(x)=-5$. Chọn khẳng định đúng.
| $\lim\limits_{x\to x_0}f(x)=\pm5$ | |
| $\lim\limits_{x\to x_0}f(x)=5$ | |
| $\lim\limits_{x\to x_0}f(x)=-5$ | |
| Không tồn tại $\lim\limits_{x\to x_0}f(x)$ |
Trong 6 khẳng định sau, có bao nhiêu khẳng định đúng?
- $\lim\limits_{x\to x_0}x=x_0$;
- $\lim\limits_{x\to+\infty}x=+\infty$;
- $\lim\limits_{x\to-\infty}x=-\infty$;
- $\lim\limits_{x\to-\infty}\dfrac{1}{x}=0$;
- $\lim\limits_{x\to+\infty}x^3=+\infty$;
- $\lim\limits_{x\to-\infty}x^2=-\infty$.
| $6$ | |
| $5$ | |
| $3$ | |
| $4$ |
Cho hàm số $f(x)=\begin{cases}4x-1\text{ khi }x>2\\ 2x+1\text{ khi }x\le 2\end{cases}$. Tính $\lim\limits_{x\to2^{-}}f(x)$.
| Không tồn tại $\lim\limits_{x\to2^{-}}f(x)$ | |
| $\lim\limits_{x\to2^{-}}f(x)=5$ | |
| $\lim\limits_{x\to2^{-}}f(x)=12$ | |
| $\lim\limits_{x\to2^{-}}f(x)=7$ |
Cho $\lim\limits_{x\to x_0}f(x)=2$, $\lim\limits_{x\to{x_0}}g(x)=3$, với $L,M\in \mathbb{R}$. Chọn khẳng định sai.
| $\lim\limits_{x\to x_0}\left[g(x)-f(x)\right]=1$ | |
| $\lim\limits_{x\to x_0}\left[f(x)+g(x)\right]=5$ | |
| $\lim\limits_{x\to x_0}\left[f(x)\cdot g(x)\right]=6$ | |
| $\lim\limits_{x\to x_0}\left[f(x)-g(x)\right]=1$ |
Cho hàm số trùng phương $f(x)=ax^4+bx^2+c$ có đồ thị như hình vẽ.
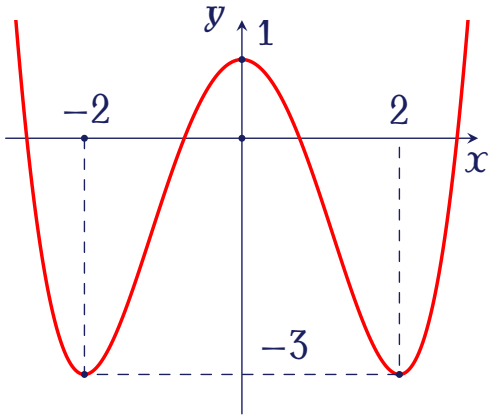
Hỏi đồ thị hàm số $y=\dfrac{2022}{\big[f(x)\big]^2+2f(x)-3}$ có tổng cộng bao nhiêu tiệm cận đứng?
| $4$ | |
| $3$ | |
| $5$ | |
| $2$ |
Tiệm cận đứng của đồ thị hàm số $y=\dfrac{2x-1}{x-3}$ là đường thẳng có phương trình
| $x=\dfrac{1}{2}$ | |
| $x=\dfrac{1}{3}$ | |
| $x=2$ | |
| $x=3$ |
Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số $y=\dfrac{x-1}{x^2-2x-3}$ là
| $4$ | |
| $3$ | |
| $2$ | |
| $1$ |
Tiệm cận đứng của đồ thị hàm số $y=\dfrac{3x-2}{x+4}$ là đường thẳng có phương trình
| $x=4$ | |
| $x=3$ | |
| $x=-3$ | |
| $x=-4$ |
Cho hàm số $y=\dfrac{ax+b}{cx+1}$ ($a,b,c\in\mathbb{R}$) có đồ thị như hình bên.
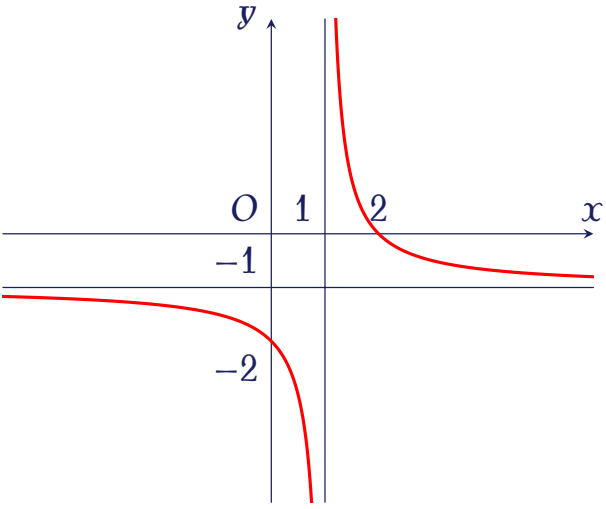
Khi đó $a+b-c$ bằng
| $-2$ | |
| $-1$ | |
| $1$ | |
| $0$ |
