Tính diện tích \(S\) của hình phẳng \((H)\) giới hạn bởi đồ thị hàm số \(y=-x^3+3x^2-2\), hai trục tọa độ và đường thẳng \(x=2\).
| \(S=\dfrac{1}{3}\) | |
| \(S=\dfrac{19}{2}\) | |
| \(S=\dfrac{9}{2}\) | |
| \(S=\dfrac{5}{2}\) |
Đồ thị hàm số $y=\dfrac{x-4}{2x+2}$ cắt trục tung tại điểm có tung độ bằng
| $\dfrac{1}{2}$ | |
| $-1$ | |
| $-2$ | |
| $4$ |
Cho hàm số $y=\dfrac{ax+b}{cx+d}$ có đồ thị là đường cong trong hình bên.
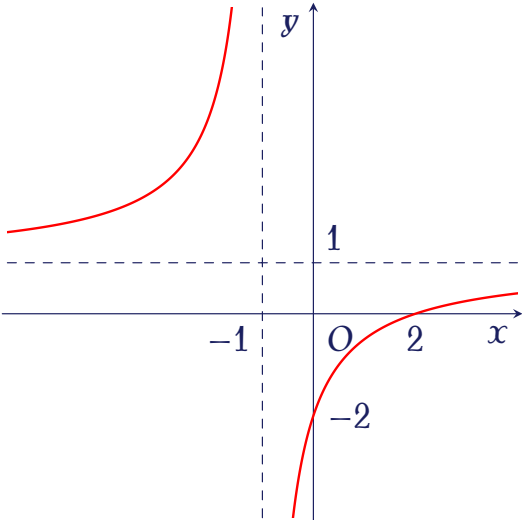
Tọa độ giao điểm của đồ thị hàm số đã cho và trục hoành là
| $(0;-2)$ | |
| $(2;0)$ | |
| $(-2;0)$ | |
| $(0;2)$ |
Cho hàm số $y=\dfrac{-x+1}{2x-1}$ có đồ thị $(\mathscr{C})$ và đường thẳng $(d)\colon y=x+m$. Với mọi giá trị thực của $m$ đường thẳng $(d)$ luôn cắt đồ thị $(\mathscr{C})$ tại hai điểm phân biệt $A$ và $B$. Gọi $k_1,\,k_2$ lần lượt là hệ số góc của các tiếp tuyến với $(\mathscr{C})$ tại $A$ và $B$. Giá trị nhỏ nhất của $T=k_1^{2022}+k_2^{2022}$ bằng
| $\dfrac{1}{2}$ | |
| $2$ | |
| $\dfrac{2}{3}$ | |
| $1$ |
Tìm các giá trị thực của tham số $m$ để đồ thị hàm số $y=x^4-2mx^2$ có ba điểm cực trị tạo thành một tam giác có diện tích bằng $4\sqrt{2}$.
| $m=2$ | |
| $m=-2$ | |
| $m=\pm2$ | |
| $m=32$ |
Tìm phương trình tiếp tuyến của đồ thị hàm số $y=f(x)=\dfrac{x-1}{x+2}$ tại điểm có tung độ bằng $2$.
| $y=-\dfrac{1}{3}x+\dfrac{1}{3}$ | |
| $y=\dfrac{1}{3}x+\dfrac{11}{3}$ | |
| $y=\dfrac{1}{3}x-\dfrac{11}{3}$ | |
| $y=\dfrac{1}{3}x+\dfrac{1}{3}$ |
Cho hàm số $y=\dfrac{2x+1}{x-1}$ có đồ thị là $(\mathscr{C})$. Viết phương trình tiếp tuyến của $(\mathscr{C})$ biết tiếp tuyến vuông góc với đường thẳng có phương trình $x-3y+2019=0$.
Diện tích hình phẳng giới hạn bởi đồ thị hàm số $y=\mathrm{e}^x$ và các đường thẳng $y=0$, $x=0$, $x=2$ bằng
| $\pi\displaystyle\displaystyle\int\limits_{0}^{2}\mathrm{e}^x\mathrm{\,d}x$ | |
| $\displaystyle\displaystyle\int\limits_{0}^{2}\mathrm{e}^{2x}\mathrm{\,d}x$ | |
| $\pi\displaystyle\displaystyle\int\limits_{0}^{2}\mathrm{e}^{2x}\mathrm{\,d}x$ | |
| $\displaystyle\displaystyle\int\limits_{0}^{2}\mathrm{e}^x\mathrm{\,d}x$ |
Cho hàm số $y=x^4-4x^2+m$. Tìm $m$ để đồ thị của hàm số cắt trục hoành tại $4$ điểm phân biệt sao cho hình phẳng giới hạn bởi đồ thị với trục hoành có diện tích phần phía trên trục hoành bằng diện tích phần phía dưới trục hoành. Khi đó $m=\dfrac{a}{b}$ với $\dfrac{a}{b}$ là phân số tối giản. Tính $a+2b$.
| $37$ | |
| $38$ | |
| $0$ | |
| $29$ |
Tiếp tuyến của đồ thị hàm số \(y=\dfrac{x-2}{2x+1}\) vuông góc với đường thẳng \(y=-\dfrac{1}{5}x\) là
| \(y=5x+3\) và \(y=5x-2\) | |
| \(y=5x-8\) và \(y=5x-2\) | |
| \(y=5x+8\) và \(y=5x-2\) | |
| \(y=5x+8\) và \(y=5x+2\) |
Tìm tất cả các phương trình tiếp tuyến của đồ thị hàm số \(y=\dfrac{2x+1}{x-1}\) song song với đường thẳng \(y=-3x+15\).
| \(y=-3x+1\), \(y=-3x-7\) | |
| \(y=-3x-1\), \(y=-3x+11\) | |
| \(y=-3x-1\) | |
| \(y=-3x+11\), \(y=-3x+5\) |
Viết phương trình tiếp tuyến của đồ thị \(y=\dfrac{x-1}{x+1}\), biết tiếp tuyến có hệ số góc là \(\dfrac{1}{2}\).
| \(y=\dfrac{1}{2}x-\dfrac{1}{2}\) và \(y=\dfrac{1}{2}x+\dfrac{7}{2}\) | |
| \(y=\dfrac{1}{2}x-\dfrac{1}{2}\) và \(y=\dfrac{1}{2}x-\dfrac{7}{2}\) | |
| \(y=\dfrac{1}{2}x+\dfrac{1}{2}\) và \(y=\dfrac{1}{2}x+\dfrac{7}{2}\) | |
| \(y=\dfrac{1}{2}x+\dfrac{1}{2}\) và \(y=\dfrac{1}{2}x-\dfrac{7}{2}\) |
Phương trình tiếp tuyến với đồ thị hàm số \(y=\dfrac{2x-4}{x-4}\) tại điểm có tung độ bằng \(3\) là
| \(x+4y-20=0\) | |
| \(x+4y-5=0\) | |
| \(4x+y-2=0\) | |
| \(4x+y-5=0\) |
Tiếp tuyến của đồ thị hàm số \(y=\dfrac{4}{x-1}\) tại điểm có hoành độ \(x_0=-1\) là
| \(y=-x-3\) | |
| \(y=x-1\) | |
| \(y=-x+2\) | |
| \(y=-x-1\) |
Phương trình tiếp tuyến của đồ thị hàm số \(y=\dfrac{2x-1}{x+1}\) tại điểm \(M(0;-1)\) là
| \(y=3x+1\) | |
| \(y=3x-1\) | |
| \(y=-3x-1\) | |
| \(y=-3x+1\) |
Tiếp tuyến của đồ thị hàm số \(y=\dfrac{x+1}{x-5}\) tại điểm \(A(-1;0)\) có hệ số góc bằng
| \(\dfrac{1}{6}\) | |
| \(-\dfrac{1}{6}\) | |
| \(\dfrac{6}{25}\) | |
| \(-\dfrac{6}{25}\) |
Tìm tọa độ giao điểm \(M\) của đồ thị hàm số \(y=\dfrac{2x-1}{x+2}\) với trục tung.
| \(M\left(\dfrac{1}{2};0\right)\) | |
| \(M\left(0;2\right)\) | |
| \(M\left(0;-\dfrac{1}{2}\right)\) | |
| \(M\left(-\dfrac{1}{2};0\right)\) |
Biết rằng đồ thị hàm số \(y=\dfrac{(m-2n-3)x+5}{x-m-n}\) nhận hai trục tọa độ làm hai đường tiệm cận. Tính tổng \(S=m^2+n^2-2\).
| \(S=2\) | |
| \(S=0\) | |
| \(S=-1\) | |
| \(S=1\) |
Tính diện tích hình phẳng giới hạn bởi \(\left(\mathscr{C}\right)\colon y=x^4-2x^2+1\) và trục hoành.
| \(\dfrac{8}{15}\) | |
| \(-\dfrac{15}{16}\) | |
| \(\dfrac{15}{8}\) | |
| \(\dfrac{16}{15}\) |
Tính diện tích hình phẳng giới hạn bởi các đường \(y=-x^2+4x-3\), \(x=0\), \(x=3\), \(Ox\).
| \(-\dfrac{8}{3}\) | |
| \(-\dfrac{4}{3}\) | |
| \(\dfrac{4}{3}\) | |
| \(\dfrac{8}{3}\) |
