Với mọi $a$, $b$ thỏa mãn $\log_2a^3+\log_2b=6$, khẳng định nào dưới đây đúng?

	$a^3b=64$
	$a^3b=36$
	$a^3+b=64$
	$a^3+b=36$

Cho hàm số $f\left(x\right)=\log_2^3x-\log_2x^3+m$ ($m$ là tham số thực). Gọi $S$ là tập hợp tất cả các giá trị của $m$ sao cho $\max\limits_{\left[1;4\right]}\left|f\left(x\right)\right|+\min\limits_{\left[1;4\right]}\left|f\left(x\right)\right|=6$. Tổng bình phương các phần tử của $S$ bằng

	$13$
	$18$
	$5$
	$8$

Cho $a,\,b$ là các số thực dương thỏa mãn $\log_{27}a=\log_3\left(a\sqrt[3]{b}\right)$. Mệnh đề nào dưới đây đúng?

	$a^2+b=1$
	$a+b^2=1$
	$ab^2=1$
	$a^2b=1$

Phương trình \(2^{x-2}=3^{x^2+2x-8}\) có một nghiệm dạng \(x=\log_ab-4\) với \(a,\,b\) là các số nguyên dương thuộc khoảng \((1;5)\). Khi đó, \(a+2b\) bằng

	\(6\)
	\(9\)
	\(14\)
	\(7\)

Kết quả của phép tính tích phân \(\displaystyle\int\limits_{0}^{1}\ln(2x+1)\mathrm{\,d}x=a\ln3+b\), (\(a,\,b\in\mathbb{Q}\)) khi đó giá trị của \(ab^3\) bằng

	\(-\dfrac{3}{2}\)
	\(3\)
	\(1\)
	\(\dfrac{3}{2}\)

Tập nghiệm của bất phương trình \(\log_2^2x-3\log_2x+2<0\) là khoảng \((a;b)\). Tính \(a^2+b^2\).

	\(16\)
	\(5\)
	\(20\)
	\(10\)

Cho \(a\log_63+b\log_62+c\log_65=a\) với \(a,\,b,\,c\) là các số hữu tỉ. Trong các khẳng định sau, khẳng định nào đúng?

	\(a=b=c\neq0\)
	\(a=c\)
	\(a=b\)
	\(b=c\)

Biết $I=\displaystyle\displaystyle\int\limits_{1}^{2}\dfrac{\mathrm{d}x}{(x+1)\sqrt{x}+x\sqrt{x+1}}=\sqrt{a}-\sqrt{b}-c$ với $a,\,b,\,c$ là các số nguyên dương. Tính $P=a+b+c$.

	$P=18$
	$P=12$
	$P=24$
	$P=46$

Cho hàm số $f(x)=\dfrac{ax-1}{bx+c}\,(a,\,b,\,c\in\mathbb{R})$ có bảng biến thiên như hình bên.

Giá trị của $a-b-c$ thuộc khoảnh nào sau đây?

	$\left(-1;0\right)$
	$\left(-2;-1\right)$
	$\left(1;2\right)$
	$\left(0;1\right)$

Trong không gian $Oxyz$, cho ba điểm $A(2;1;0)$, $B(0;2;1)$, $C(1;3;-1)$. Điểm $M(a;b;c)\in(Oxy)$ sao cho $\big|2\overrightarrow{MA}+3\overrightarrow{MB}-4\overrightarrow{MC}\big|$ đạt giá trị nhỏ nhất. Mệnh đề nào sau đây đúng?

	$a+b+c=3$
	$a+b+c=-3$
	$a+b+c=-4$
	$a+b+c=10$

Trong không gian $Oxyz$, gọi mặt phẳng $(P)\colon7x+by+cz+d=0$ (với $b,\,c,\,d\in\mathbb{R}$, $c< 0$) đi qua điểm $A(1;3;5)$. Biết mặt phẳng $(P)$ song song với trục $Oy$ và khoảng cách từ gốc tọa độ đến mặt phẳng $(P)$ bằng $3\sqrt{2}$. Tính $T=b+c+d$.

	$T=61$
	$T=78$
	$T=7$
	$T=-4$

Cho $\displaystyle\displaystyle\int\limits_{\tfrac{\pi}{6}}^{\tfrac{\pi}{4}}\cos4x\cos x\mathrm{\,d}x=\dfrac{\sqrt{2}}{a}+\dfrac{b}{c}$ với $a,\,b,\,c$ là các số nguyên, $c< 0$ và $\dfrac{b}{c}$ tối giản. Tổng $a+b+c$ bằng

	$-77$
	$-17$
	$103$
	$43$

Trong không gian $Oxyz$ cho mặt phẳng $(\alpha)\colon2x+2y-z-6=0$. Gọi mặt phẳng $(\beta)\colon x+y+cz+d=0$ không qua $O$, song song với mặt phẳng $(\alpha)$ và $\mathrm{d}\left((\alpha),(\beta)\right)=2$. Tính $c\cdot d$?

	$cd=3$
	$cd=0$
	$cd=12$
	$cd=6$

Biết $\displaystyle\displaystyle\int\limits_0^1x\sqrt{x^2+4}\mathrm{\,d}x=\dfrac{1}{a}\left(\sqrt{b^3}-c\right)$. Tính $Q=abc$.

	$Q=120$
	$Q=15$
	$Q=-120$
	$Q=40$

Trong không gian $Oxyz$, cho hai điểm $A(2;1;3)$ và $B(6;5;5)$. Xét khối nón $(N)$ có đỉnh $A$, đường tròn đáy nằm trên mặt cầu đường kính $AB$. Khi $(N)$ có thể tích lớn nhất thì mặt phẳng chứa đường tròn đáy của $(N)$ có phương trình dạng $2x+by+cz+d=0$. Giá trị của $b+c+d$ bằng

	$-21$
	$-12$
	$-18$
	$-15$

Cho $\left(\dfrac{2x^2-3x+5}{x-3}\right)^{\prime}=\dfrac{ax^2-bx+c}{\left(x-3\right)^2}$. Tính $S=a+b+c$. 

	$S=0$
	$S=12$
	$S=-6$
	$S=18$

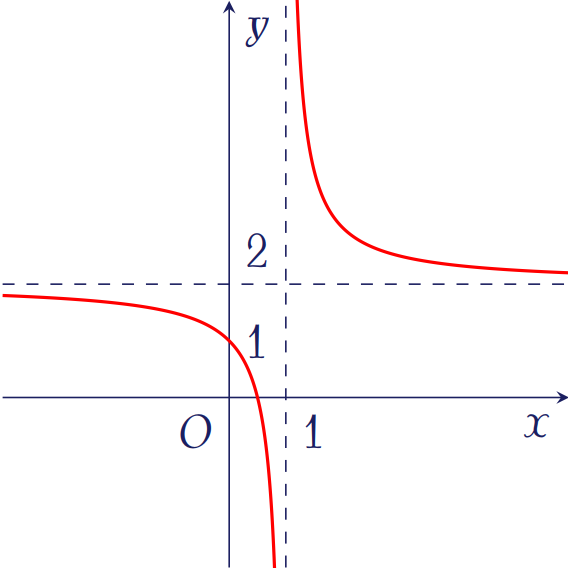
Cho hàm số \(y=\dfrac{ax-1}{bx+c}\) có đồ thị như hình trên. Tính giá trị biểu thức \(T=a+2b+3c\).

	\(T=1\)
	\(T=2\)
	\(T=3\)
	\(T=4\)

Biết \(\displaystyle\int\limits_{1}^{2}\dfrac{\mathrm{d}x}{(x+1)(2x+1)}=a\ln2+b\ln3+c\ln5\). Khi đó giá trị \(a+b+c\) bằng

	\(1\)
	\(0\)
	\(2\)
	\(-3\)

Cho \(\displaystyle\int\limits_{0}^{1}\dfrac{x^2+1}{x+1}\mathrm{\,d}x=a+b\ln c\), với \(a\in\mathbb{Q}\), \(b\in\mathbb{Z}\), \(c\) là số nguyên tố. Ta có \(2a+b+c\) bằng

	\(5\)
	\(4\)
	\(3\)
	\(2\)

Trong không gian với hệ tọa độ \(Oxyz\), cho mặt cầu \(\left(S\right)\colon\left(x-1\right)^2+\left(y-2\right)^2+\left(z-3\right)^2=16\) và các điểm \(A\left(1;0;2\right)\), \(B\left(-1;2;2\right)\). Gọi \((P)\) là mặt phẳng đi qua hai điểm \(A,\,B\) sao cho thiết diện của mặt phẳng \((P)\) với mặt cầu \((S)\) có diện tích nhỏ nhất. Khi viết phương trình \((P)\) dưới dạng \(ax+by+cx+3=0\). Tính tổng \(T=a+b+c\).

	\(-2\)
	\(-3\)
	\(0\)
	\(3\)