Cho ba số thực dương $A,\,B,\,C$ khác $1$ thỏa $B^2=AC$. Mệnh đề nào sau đây đúng?
| $\ln A+\ln C=2\ln B$ | |
| $\ln A\cdot\ln C=2\ln B$ | |
| $\ln A\cdot\ln C=\big(\ln B\big)^2$ | |
| $\ln A+\ln C=\ln B$ |
Cho mọi số thực dương $a,\,b$ thỏa mãn $\log_3a=\log_{27}\left(a^2\sqrt{b}\right)$. Khẳng định nào sau đây đúng?
| $a^2=b$ | |
| $a^3=b$ | |
| $a=b$ | |
| $a=b^2$ |
Với mọi $a,\,b$ thỏa mãn $\log_2a-3\log_2b=2$, khẳng định nào dưới đây đúng?
| $a=4b^3$ | |
| $a=3b+4$ | |
| $a=3b+2$ | |
| $a=\dfrac{4}{b^3}$ |
Xét các số thực \(a,\,b\) thỏa mãn \(\log_3\left(3^a\cdot9^b\right)=\log_93\). Mệnh đề nào là đúng?
| \(a+2b=2\) | |
| \(4a+2b=1\) | |
| \(4ab=1\) | |
| \(2a+4b=1\) |
Xét tất cả các số thực dương \(a\) và \(b\) thỏa mãn $$\log_2a=\log_8\left(ab\right).$$Mệnh đề nào dưới đây đúng?
| \(a=b^2\) | |
| \(a^3=b\) | |
| \(a=b\) | |
| \(a^2=b\) |
Với các số thực dương \(a,\,b\) thỏa mãn \(a^2+b^2=6ab\), biểu thức \(\log_2(a+b)\) bằng
| \(\dfrac{1}{2}\left(3+\log_2a+\log_2b\right)\) | |
| \(\dfrac{1}{2}\left(1+\log_2a+\log_2b\right)\) | |
| \(1+\dfrac{1}{2}\left(\log_2a+\log_2b\right)\) | |
| \(2+\dfrac{1}{2}\left(\log_2a+\log_2b\right)\) |
Cho hai số thực dương \(a,\,b\) thỏa mãn \(a^2+b^2=8ab\). Mệnh đề nào sau đây đúng?
| \(\log(a+b)=\dfrac{1}{2}\left(\log a+\log b\right)\) | |
| \(\log(a+b)=\dfrac{1}{2}\left(1+\log a +\log b\right)\) | |
| \(\log(a+b)=1+\log a+\log b\) | |
| \(\log(a+b)=\dfrac{1}{2}+\log a+\log b\) |
Cho hình hộp $ABCD.A'B'C'D'$. Chọn khẳng định đúng.
| $\overrightarrow{BD}-\overrightarrow{D'D}-\overrightarrow{B'D'}=\overrightarrow{BB'}$ | |
| $\overrightarrow{BD}-\overrightarrow{D'D}-\overrightarrow{B'D'}=\overrightarrow{AC'}$ | |
| $\overrightarrow{BD}-\overrightarrow{D'D}-\overrightarrow{B'D'}=\overrightarrow{CD}$ | |
| $\overrightarrow{BD}-\overrightarrow{D'D}-\overrightarrow{B'D'}=\overrightarrow{AC}$ |
Cho hình lăng trụ $ABC.A'B'C'$. Chọn khẳng định đúng.
| $\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{AA'}=\overrightarrow{AB}$ | |
| $\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{AA'}=\overrightarrow{AC'}$ | |
| $\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{AA'}=\overrightarrow{AB'}$ | |
| $\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{AA'}=\overrightarrow{AC}$ |
Cho $a$ và $b$ là hai số thực dương khác $1$ và các hàm số $y=a^x$, $y=b^x$ có đồ thị như hình bên.
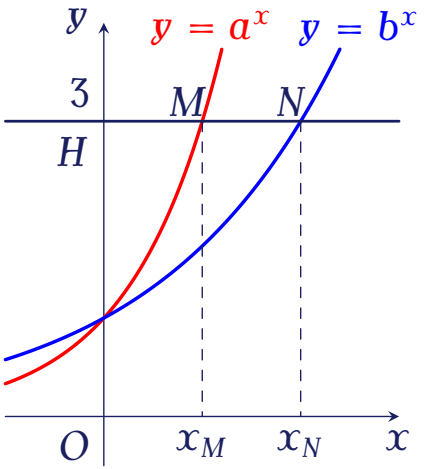
Đường thẳng $y=3$ cắt trục tung, đồ thị hàm số $y=a^x$, đồ thị hàm số $y=b^x$ lần lượt tại $H,\,M,\,N$. Biết rằng $HM=2MN$. Mệnh đề nào sau đây đúng?
| $a^2=b^3$ | |
| $3a=2b$ | |
| $a^3=b^2$ | |
| $2a=b$ |
Với mọi số nguyên dương $n$, để chứng minh $\dfrac{1}{1\cdot3}+\dfrac{1}{3\cdot5}+\cdots+\dfrac{1}{(2n-1)(2n+1)}=\dfrac{n}{2n+1}$ bằng phương pháp quy nạp toán học, sau giả thiết quy nạp ta cần chứng minh điều gì?
| $\dfrac{1}{1\cdot3}+\dfrac{1}{3\cdot5}+\cdots+\dfrac{1}{(2k-1)(2k+1)}+\dfrac{1}{(2k+1)(2k+3)}=\dfrac{k+1}{2k+3}$ | |
| $\dfrac{1}{1\cdot3}+\dfrac{1}{3\cdot5}+\cdots+\dfrac{1}{(2k-1)(2k+1)}=\dfrac{k+1}{2k+3}$ | |
| $\dfrac{1}{1\cdot3}+\dfrac{1}{3\cdot5}+\cdots+\dfrac{1}{(2k-1)(2k+1)}=\dfrac{k}{2k+1}$ | |
| $\dfrac{1}{1\cdot3}+\dfrac{1}{3\cdot5}+\cdots+\dfrac{1}{(2k-1)(2k+1)}+\dfrac{1}{(2k+1)(2k+3)}=\dfrac{k}{2k+1}$ |
Với mọi số nguyên dương $n$, đặt $S_n=\dfrac{1}{1\cdot3}+\dfrac{1}{3\cdot5}+\cdots+\dfrac{1}{(2n-1)(2n+1)}$. Để chứng minh $S_n=\dfrac{n}{2n+1}$ bằng phương pháp quy nạp toán học, sau giả thiết quy nạp ta cần chứng minh điều gì?
| $S_{k+1}=\dfrac{k+1}{2k+3}$ | |
| $S_{k+1}=\dfrac{k}{2k+1}$ | |
| $S_k=\dfrac{k}{2k+1}$ | |
| $S_{k+1}=\dfrac{k+1}{2k+1}$ |
Cho hàm số $y=\dfrac{1}{x}$. Khẳng định nào dưới đây là đúng?
| $y''y^3+2=0$ | |
| $y''y=2\left(y'\right)^2$ | |
| $y''y+2\left(y'\right)^2=0$ | |
| $y''y^3=2$ |
Cho hàm số $y=\sin2x$. Khẳng định nào sau đây là đúng?
| $y^2-\left(y'\right)^2=4$ | |
| $4y+y''=0$ | |
| $4y-y''=0$ | |
| $y=y'.\tan2x$ |
Cho hàm số $y=\sin^2x$. Khẳng định nào sau đây đúng?
| $2y'+y''=\sqrt{2}\cos\left(2x-\dfrac{\pi}{4}\right)$ | |
| $2y+y'.\tan x=0$ | |
| $4y-y''=2$ | |
| $4y'+y'''=0$ |
Chứng minh rằng $$1+3+6+\cdots+\dfrac{n(n+1)}{2}=\dfrac{n(n+1)(n+2)}{6},\text{ }\forall n\in\Bbb{N}^*$$
Chứng minh rằng $$2+5+8+\cdots+(3n-1)=\dfrac{n(3n+1)}{2},\text{ }\forall n\in\Bbb{N}^*$$
Chứng minh rằng $$1^2+3^2+5^2+\cdots+(2n-1)^2=\dfrac{n(4n^2-1)}{3},\,\,\forall n\in\Bbb{N}^*$$
Chứng minh rằng $$1^2+2^2+3^2+\cdots+n^2=\dfrac{n(n+1)(2n+1)}{6},\text{ }\forall n\in\Bbb{N}^*$$
Chứng minh rằng $$1+3+5+\cdots+(2n-1)=n^2,\text{ }\forall n\in\Bbb{N}^*$$
