Đồ thị hàm số \(y=\dfrac{x^2+2x+3}{\sqrt{x^4-3x^2+2}}\) có bao nhiêu đường tiệm cận?

	\(4\)
	\(5\)
	\(3\)
	\(6\)

Đồ thị hàm số \(y=\dfrac{x+1}{\sqrt{x^2-1}}\) có bao nhiêu đường tiệm cận?

	\(3\)
	\(1\)
	\(2\)
	\(0\)

Số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số \(y=\dfrac{\sqrt{x+1}-1}{x^3-4x}\) lần lượt là

	\(3\) và \(1\)
	\(1\) và \(1\)
	\(2\) và \(1\)
	\(1\) và \(0\)

Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số $y=\dfrac{x-1}{x^2-2x-3}$ là

	$4$
	$3$
	$2$
	$1$

Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số $y=\dfrac{x-1}{x^2-2x-3}$ là

	$4$
	$3$
	$2$
	$1$

Đồ thị hàm số nào dưới đây không có đường tiệm cận?

	\(y=\dfrac{x}{x^2+1}\)
	\(y=\dfrac{1}{x}\)
	\(y=x^4-3x^2+2\)
	\(y=\dfrac{2x+1}{2-x}\)

Đồ thị hàm số nào sau đây có \(3\) đường tiệm cận?

	\(y=\dfrac{1-2x}{1+x}\)
	\(y=\dfrac{1}{4-x^2}\)
	\(y=\dfrac{x+3}{5x-1}\)
	\(y=\dfrac{x}{x^2-x+9}\)

Đồ thị hàm số \(y=\dfrac{x+2021}{\sqrt{x^2-1}}\) có bao nhiêu đường tiệm cận ngang?

	\(4\)
	\(1\)
	\(3\)
	\(2\)

Cho hàm số \(y=\dfrac{5x+5}{x^2-1}\). Gọi \(m\) là số tiệm cận đứng, \(n\) là số tiệm cận ngang của đồ thị hàm số đã cho. Tính \(S=m+n\).

	\(S=2\)
	\(S=3\)
	\(S=1\)
	\(S=4\)

Đồ thị hàm số \(y=\dfrac{x^2+x-2}{x^2-3x+2}\) có tất cả bao nhiêu đường tiệm cận?

	\(3\)
	\(0\)
	\(1\)
	\(2\)

Đồ thị hàm số \(y=\dfrac{4x+4}{x^2+2x+1}\) có tất cả bao nhiêu đường tiệm cận?

	\(2\)
	\(0\)
	\(1\)
	\(3\)

Số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số \(y=\dfrac{2x^2+2x}{x^2+2x+1}\) lần lượt là

	\(0\) và \(2\)
	\(0\) và \(1\)
	\(1\) và \(2\)
	\(1\) và \(1\)

Đồ thị hàm số nào sau đây có đúng $1$ đường tiệm cận ngang?

	$y=\dfrac{\sqrt{2-x^2}}{x+3}$
	$y=\dfrac{4x-3}{x^2-2x}$
	$y=\dfrac{\sqrt{x^2+1}}{5x-3}$
	$y=\dfrac{x^2-x}{x+1}$

Đồ thị hàm số nào sau đây có tiệm cận ngang?

	$y=\dfrac{1-x^2}{x}$
	$y=\dfrac{\sqrt{x^2-1}}{x}$
	$y=\dfrac{x^2-1}{x}$
	$y=\dfrac{\sqrt{1-x^2}}{x}$

Tìm tất cả các giá trị thực của tham số $m$ sao cho đồ thị hàm số $y=\dfrac{2x-\sqrt{mx^2+1}}{x-1}$ có đúng hai đường tiệm cận ngang.

	$m<0$
	$0<m<3$ hoặc $m>3$
	$m>0$
	$m=0$

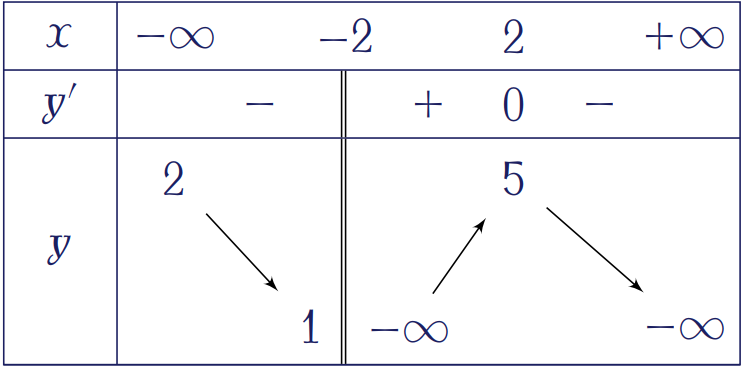
Cho hàm số \(y=f(x)\) có bảng biến thiên như hình trên. Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là

	\(4\)
	\(2\)
	\(3\)
	\(1\)

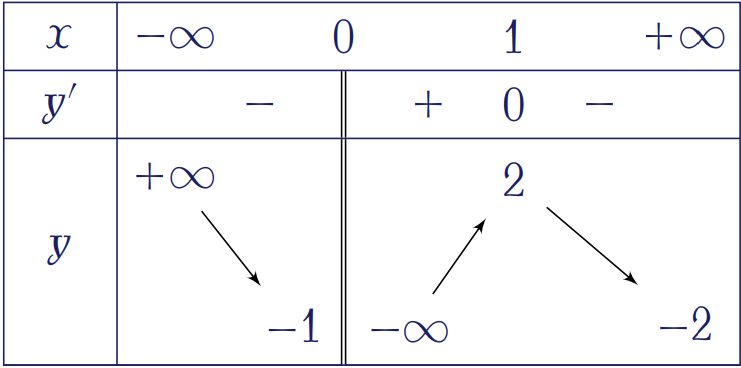
Cho hàm số \(y=f(x)\) có bảng biến thiên như hình trên. Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là

	\(3\)
	\(4\)
	\(1\)
	\(2\)

Tìm số đường tiệm cận đứng của đồ thị hàm số \(y=\dfrac{x^2-3x-4}{x^2-16}\).

	\(1\)
	\(2\)
	\(0\)
	\(3\)

Đồ thị của hàm số nào dưới đây có tiệm cận đứng?

	\(y=\dfrac{\sqrt{1-x^2}+1}{2019}\)
	\(y=\dfrac{x^2-1}{x-1}\)
	\(y=\dfrac{x^2}{x^2+2018}\)
	\(y=\dfrac{x}{x+12}\)

Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số \(y=\dfrac{5x^2-4x-1}{x^2-1}\) là

	\(1\)
	\(0\)
	\(2\)
	\(3\)