Hàm số $y=\dfrac{1}{3}x^3-mx^2+\big(m^2-m-1\big)x+m^3$ đạt cực đại tại điểm $x=1$ thì giá trị của tham số $m$ bằng
| $\left[\begin{array}{l}m=0\\ m=3\end{array}\right.$ | |
| $m=0$ | |
| $m=-3$ | |
| $m=3$ |
Có tât cả bao nhiêu giá trị nguyên của tham số $m$ để hàm số $y=\dfrac{1}{3}x^3-mx^2+9x-1$ đồng biến trên $\mathbb{R}$?
| $8$ | |
| $9$ | |
| $7$ | |
| $6$ |
Số giá trị nguyên của tham số $m$ để hàm số $y=x^3-(m+1)x^2+3x+1$ đồng biến trên $\mathbb{R}$ là
| $4$ | |
| $6$ | |
| $5$ | |
| $7$ |
Cho hàm số $f(x)=ax^3+bx^2+cx+d$ ($a\neq0$) có đồ thị là đường cong trong hình bên.
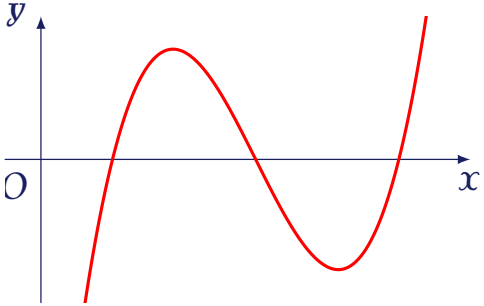
Số các giá trị nguyên của tham số $m\in(-2019;2023]$ để phương trình $4^{f(x)}-(m-1)2^{f(x)+1}+2m-3=0$ có đúng ba nghiệm là
| $2020$ | |
| $2019$ | |
| $2021$ | |
| $2022$ |
Có bao nhiêu giá trị nguyên của tham số $m$ sao cho ứng với mỗi $m$, hàm số $y=-x^3+3x^2-3mx+\dfrac{5}{3}$ có đúng một cực trị thuộc khoảng $(-2;5)$?
| $16$ | |
| $6$ | |
| $17$ | |
| $7$ |
Có bao nhiêu giá trị nguyên của tham số a thuộc đoạn $[-10;10]$ để hàm số $$y=\big|-x^3+3(a+1)x^2-3a(a+2)x+a^2(a+3)\big|$$đồng biến trên khoảng $(0;1)$
| $21$ | |
| $10$ | |
| $8$ | |
| $2$ |
Có bao nhiêu giá trị nguyên của tham số $a\in(-10;+\infty)$ để hàm số $y=\big|x^3+(a+2)x+9-a^2\big|$ đồng biến trên khoảng $(0;1)$?
| $12$ | |
| $11$ | |
| $6$ | |
| $5$ |
Cho hàm số bậc ba $y=f(x)$ có đồ thị là đường cong trong hình bên.
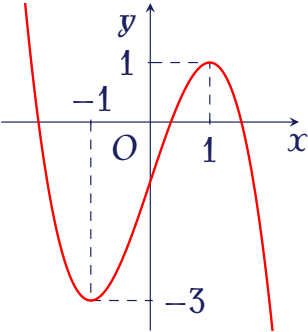
Có bao nhiêu giá trị nguyên của tham số $m$ để phương trình $f(x)=m$ có ba nghiệm thực phân biệt?
| $2$ | |
| $5$ | |
| $3$ | |
| $4$ |
Có tất cả bao nhiêu giá trị nguyên của tham số $m$ để hàm số $y=\dfrac{1}{3}x^3-mx^2+9x-1$ đồng biến trên $\mathbb{R}$?
| $8$ | |
| $9$ | |
| $7$ | |
| $6$ |
Tìm các giá trị thực của tham số $m$ để hàm số $f(x)=-x^3-3x+m$ có giá trị nhỏ nhất trên đoạn $[-1;1]$ bằng $0$.
| $m=-4$ | |
| $m=-2$ | |
| $m=2$ | |
| $m=4$ |
Gọi $x_1,\,x_2$ là hai điểm cực trị của hàm số $y=4x^3+mx^2-3x$. Tìm các giá trị của tham số $m$ sao cho $x_1+4x_2=0$.
| $m=0$ | |
| $m=\pm\dfrac{9}{2}$ | |
| $m=\pm\dfrac{3}{2}$ | |
| $m=\pm\dfrac{1}{2}$ |
Gọi $x_1,\,x_2$ là hai điểm cực trị của hàm số $y=x^3-3mx^2+3\big(m^2-1\big)x-m^3+m$. Tìm các giá trị của tham số $m$ sao cho $x_1^2+x_2^2-x_1x_2=7$.
| $m=0$ | |
| $m=\pm\dfrac{9}{2}$ | |
| $m=\pm\dfrac{1}{2}$ | |
| $m=\pm2$ |
Gọi $S$ là tập hợp các giá trị nguyên để hàm số $y=\dfrac{x^3}{3}-(m+1)x^2+(m-2)x+2m-3$ đạt cực trị tại hai điểm $x_1,\,x_2$ thỏa mãn $x_1^2+x_2^2=18$. Tính tổng $P$ của tất cả các giá trị $m$ trong $S$.
| $P=-4$ | |
| $P=1$ | |
| $P=-\dfrac{3}{2}$ | |
| $P=-5$ |
Tìm giá trị của tham số $m$ để hàm số $y=x^3-3x^2+mx-1$ có hai điểm cực trị $x_1,\,x_2$ thỏa mãn $x_1^2+x_2^2=6$.
| $m=1$ | |
| $m=-1$ | |
| $m=3$ | |
| $m=-3$ |
Tìm tất cả các giá trị thực của tham số $m$ sao cho hàm số $y=\dfrac{mx^3}{3}+7mx^2+14x-m+2$ nghịch biến trên $[1;+\infty)$.
| $\left(-\infty;-\dfrac{14}{15}\right)$ | |
| $\left(-\infty;-\dfrac{14}{15}\right]$ | |
| $\left[-2;-\dfrac{14}{15}\right]$ | |
| $\left[-\dfrac{14}{15};+\infty\right)$ |
Tìm tập hợp giá trị của tham số $m$ để hàm số $y=x^3-mx^2-(m-6)x+1$ đồng biến trên khoảng $(0;4)$.
| $(-\infty;6]$ | |
| $(-\infty;3]$ | |
| $(-\infty;3)$ | |
| $[3;6]$ |
Cho hàm số $f(x)=x^3+ax^2+bx+c$ với $a,\,b,\,c$ là các số thực. Biết hàm số $g(x)=f(x)+f'(x)+f''(x)$ có hai giá trị cực trị là $-3$ và $6$. Diện tích hình phẳng giới hạn bởi các đường $y=\dfrac{f(x)}{g(x)+6}$ và $y=1$ bằng
| $2\ln3$ | |
| $\ln3$ | |
| $\ln18$ | |
| $2\ln2$ |
Cho hàm số $f(x)=ax^3+bx^2-36x+c$ ($a\neq0$, $a,\,b,\,c\in\mathbb{R}$), có hai điểm cực trị là $-6$ và $2$. Gọi $y=g(x)$ là đường thẳng đi qua hai điểm cực trị của đồ thị hàm số $y=f(x)$. Diện tích hình phẳng giới hạn bởi hai đường $y=f(x)$ và $y=g(x)$ bằng
| $160$ | |
| $672$ | |
| $128$ | |
| $64$ |
Cho hàm số $f\left(x\right)=x^3-2x^2+mx-3$ . Tìm $m$ để $f'\left(x\right)< 0$ với mọi $x\in\left(0;2\right)$.
Gọi $M(a;b)$ là điểm thuộc đồ thị hàm số $y=f(x)=x^3-3x^2+2$ $(\mathscr{C})$ sao cho tiếp tuyến của $(\mathscr{C})$ tại điểm $M$ có hệ số góc nhỏ nhất. Tính $a+b$.
| $-3$ | |
| $0$ | |
| $1$ | |
| $2$ |
