Cho hình chóp $S.ABC$ có góc tạo bởi các mặt bên và mặt đáy bằng nhau. Gọi $H$ là hình chiếu vuông góc của $S$ trên mặt đáy. Phát biểu nào sau đây đúng nhất?
| $S.ABC$ là hình chóp đều | |
| $H$ là trực tâm của $\triangle ABC$ | |
| $H$ là tâm đường tròn ngoại tiếp $\triangle ABC$ | |
| $H$ là tâm đường tròn nội tiếp $\triangle ABC$ |
Cho hình chóp $S.ABC$ có góc tạo bởi các cạnh bên và mặt đáy bằng nhau. Gọi $H$ là hình chiếu vuông góc của $S$ trên mặt đáy. Phát biểu nào sau đây đúng nhất?
| $S.ABC$ là hình chóp đều | |
| $H$ là trực tâm của $\triangle ABC$ | |
| $H$ là tâm đường tròn ngoại tiếp $\triangle ABC$ | |
| $H$ là tâm đường tròn nội tiếp $\triangle ABC$ |
Cho khối chóp $S.ABC$ có đáy là tam giác vuông cân tại $A$, $AB=2$, $SA$ vuông góc với đáy và $SA=3$ (tham khảo hình bên).
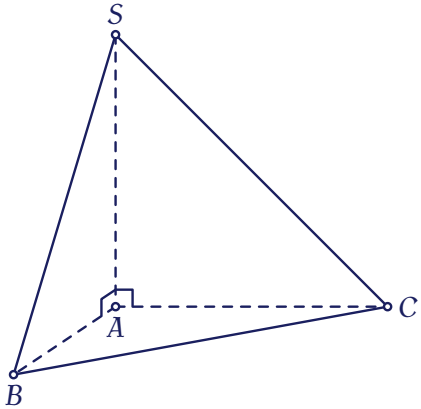
Thể tích khối chóp đã cho bằng
| $12$ | |
| $2$ | |
| $6$ | |
| $4$ |
Cho hình chóp $S.ABC$ có tam giác $ABC$ vuông cân tại $A$, $AB=AC=a$ và $SA=SB=SC=a$. Tính $\overrightarrow{AB}\cdot\overrightarrow{SC}$.
| $\overrightarrow{AB}\cdot\overrightarrow{SC}=-\dfrac{a^2}{2}$ | |
| $\overrightarrow{AB}\cdot\overrightarrow{SC}=\dfrac{a^2}{2}$ | |
| $\overrightarrow{AB}\cdot\overrightarrow{SC}=\dfrac{a^2\sqrt{3}}{2}$ | |
| $\overrightarrow{AB}\cdot\overrightarrow{SC}=-\dfrac{a^2\sqrt{3}}{2}$ |
Cho hình chóp $S.ABC$ có tam giác $SBC$ là tam giác vuông cân tại $S$, cạnh $SB=2a$ và khoảng cách từ $A$ đến mặt phẳng $(SBC)$ là $3a$. Tính theo $a$ thể tích $V$ của khối chóp $S.ABC$.
| $V=2a^3$ | |
| $V=4a^3$ | |
| $V=6a^3$ | |
| $V=12a^3$ |
Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác vuông cận tại $B$ và $BC=a$. Cạnh bên $SA=2a$ và vuông góc với mặt phẳng đáy. Tính theo $a$ thể tích $V$ của khối chóp $S.ABC$.
| $V=a^3$ | |
| $V=\dfrac{a^3\sqrt{3}}{2}$ | |
| $V=\dfrac{a^3}{3}$ | |
| $V=\dfrac{2a^3}{3}$ |
Cho hình chóp \(S.ABC\) có ba cạnh \(AS,\,AB,\,AC\) đôi một vuông góc và có độ dài bằng \(a\sqrt{2}\).
- Tính thể tích khối chóp
- Tính khoảng cách từ điểm \(A\) đến mặt phẳng \((SBC)\).
Cho tứ diện $OABC$ có $OA$, $OB$, $OC$ đôi một vuông góc. Gọi $OH$ là đường cao của tứ diện. Khi đó $H$ là
| Trọng tâm $\triangle ABC$ | |
| Trực tâm $\triangle ABC$ | |
| Tâm đường tròn nội tiếp $\triangle ABC$ | |
| Tâm đường tròn ngoại tiếp $\triangle ABC$ |
Hình nào dưới đây có tất cả các mặt bằng nhau?
| Tứ diện đều và hình lập phương | |
| Hình chóp đều và hình lập phương | |
| Hình chóp đều và lăng trụ đều | |
| Hình lập phương và hình hộp chữ nhật |
Cho hình chóp $S.ABC$ có $SA=SB=SC$ và $H$ là hình chiếu vuông góc của $S$ trên mặt phẳng $\left(ABC\right)$. Phát biểu nào sau đây không đúng?
| $H$ là tâm đường tròn ngoại tiếp tam giác $ABC$ | |
| $S.ABC$ là hình chóp đều | |
| $\widehat{SAH}=\widehat{SBH}=\widehat{SCH}$ | |
| $HA=HB=HC$ |
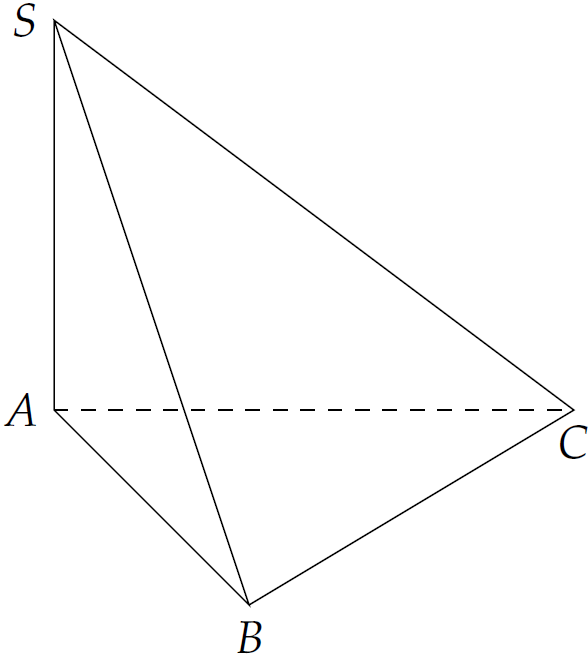
Cho hình chóp \(S.ABC\) có \(SA\) vuông góc với mặt phẳng \(\left(ABC\right)\), \(SA=a\sqrt{2}\), tam giác \(ABC\) vuông cân tại \(B\) và \(AC=2a\) (minh họa như hình trên). Góc giữa đường thẳng \(SB\) và mặt phẳng \(\left(ABC\right)\) bằng
| \(30^\circ\) | |
| \(45^\circ\) | |
| \(60^\circ\) | |
| \(90^\circ\) |
Cho khối chóp tứ giác đều $S.ABCD$ có cạnh đáy bằng $a$, cạnh bên hợp với đáy một góc $60^\circ$. Gọi $M$ là điểm đối xứng với $C$ qua $D$, $N$ là trung điểm $SC$. Mặt phẳng $(BMN)$ chia khối chóp thành hai khối đa diện. Tính thể tích $V$ của khối đa diện chứa đỉnh $C$.
| $V=\dfrac{7\sqrt{6}a^3}{72}$ | |
| $V=\dfrac{7\sqrt{6}a^3}{36}$ | |
| $V=\dfrac{5\sqrt{6}a^3}{36}$ | |
| $V=\dfrac{5\sqrt{6}a^3}{72}$ |
Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác vuông tại $A$, $\widehat{ABC}=30^\circ$. Tam giác $SBC$ là tam giác đều cạnh $a$ và nằm trong mặt phẳng vuông góc với đáy. Thể tích khối chóp $S.ABC$ là
| $\dfrac{3a^3}{16}$ | |
| $\dfrac{a^3}{16}$ | |
| $\dfrac{a^3\sqrt{3}}{16}$ | |
| $\dfrac{3\sqrt{3}a^3}{16}$ |
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình bình hành và có thể tích bằng $1$. Trên cạnh $SC$ lấy điểm $E$ sao cho $SE=2EC$. Tính thể tích $V$ của khối tứ diện $SEBD$.
| $V=\dfrac{1}{12}$ | |
| $V=\dfrac{1}{3}$ | |
| $V=\dfrac{1}{6}$ | |
| $V=\dfrac{2}{3}$ |
Cho hình chóp tứ giác đều $S.ABCD$ có cạnh đáy bằng $a$ và chiều cao bằng $2a$, diện tích xung quanh của hình nón đỉnh $S$ và đáy là hình tròn nội tiếp $ABCD$ bằng
| $\dfrac{\pi a^2\sqrt{17}}{8}$ | |
| $\dfrac{\pi a^2\sqrt{15}}{4}$ | |
| $\dfrac{\pi a^2\sqrt{17}}{4}$ | |
| $\dfrac{\pi a^2\sqrt{17}}{6}$ |
Cho khối chóp tứ giác đều có chiều cao bằng $6$ và thể tích bằng $8$. Độ dài cạnh đáy bằng
| $3$ | |
| $\dfrac{2}{\sqrt{3}}$ | |
| $4$ | |
| $2$ |
Cho khối tứ diện $ABCD$. Hai điểm $M,\,N$ lần lượt là trung điểm của $BC$ và $BD$. Mặt phẳng $(AMN)$ chia khối tứ diện $ABCD$ thành
| Một khối tứ diện và một khối chóp tứ giác | |
| Hai khối chóp tứ giác | |
| Hai khối tứ diện | |
| Hai khối tứ diện và một khối chóp tứ giác |
Cho khối chóp tứ giác đều $S.ABCD$ có cạnh đáy bằng $a$. Biết diện tích tứ giác $ABCD$ bằng ba lần diện tích tam giác $SAB$. Tính thể tích khối chóp đã cho.
| $\dfrac{a^3\sqrt{7}}{18}$ | |
| $\dfrac{a^3\sqrt{7}}{6}$ | |
| $\dfrac{a^3\sqrt{7}}{3}$ | |
| $\dfrac{a^3\sqrt{7}}{12}$ |
Cho hình chóp $S.ABC$ có đáy là tam giác đều cạnh $a$. Hình chiếu của điểm $S$ trên mặt phẳng $(ABC)$ là điểm $H$ trên cạnh $AC$ thỏa mãn $AH=\dfrac{2}{3}AC$. Đường thẳng $SC$ tạo với mặt phẳng $(ABC)$ một góc bằng $60^\circ$. Thể tích của khối chóp $S.ABC$ bằng
| $\dfrac{a^3\sqrt{3}}{12}$ | |
| $\dfrac{a^3}{12}$ | |
| $\dfrac{a^3}{9}$ | |
| $\dfrac{a^3\sqrt{2}}{9}$ |
Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác vuông tại $A$, $AB=a$, $AC=2a$, $SA$ vuông góc với mặt phẳng đáy và $SB$ tạo với mặt đáy một góc $60^\circ$. Gọi $M,\,N$ lần lượt là trung điểm của $SB$ và $BC$. Thể tích khối chóp $A.SCNM$ bằng
| $\dfrac{\sqrt{3}}{4}a^3$ | |
| $\dfrac{\sqrt{3}}{2}a^3$ | |
| $\dfrac{3\sqrt{3}}{4}a^3$ | |
| $\dfrac{3\sqrt{3}}{2}a^3$ |
