Tìm $m$ để phương trình $(m-2)x^2+3mx+m^2-4m+3=0$ có hai nghiệm trái dấu.
Biết phương trình $z^2+mz+n=0$ ($m,\,n\in\mathbb{R}$) có một nghiệm là $1-3i$. Tính $n+3m$.
| $4$ | |
| $3$ | |
| $16$ | |
| $6$ |
Giả sử phương trình $2x^2-4ax-1=0$ có hai nghiệm $x_1,\,x_2$. Tính giá trị của biểu thức $T=\left|x_1-x_2\right|$.
| $T=\dfrac{4a^2+2}{3}$ | |
| $T=\sqrt{4a^2+2}$ | |
| $T=\dfrac{\sqrt{a^2+8}}{2}$ | |
| $T=\dfrac{\sqrt{a^2+8}}{4}$ |
Tìm các giá trị thực của tham số $m$ để phương trình $$\left(x-1\right)\left(x^2-4mx-4\right)=0$$có ba nghiệm phân biệt.
| $m\in\Bbb{R}$ | |
| $m\neq0$ | |
| $m\neq\dfrac{3}{4}$ | |
| $m\neq-\dfrac{3}{4}$ |
Phương trình $\left(m-1\right)x^2+6x-1=0$ có hai nghiệm phân biệt khi
| $m>-8$ | |
| $m>-\dfrac{5}{4}$ | |
| $\begin{cases}m>-8\\ m\neq1\end{cases}$ | |
| $\begin{cases}m>-\dfrac{5}{4}\\ m\neq1\end{cases}$ |
Tìm các giá trị của $m$ để phương trình $-2x^2-4x+3=m$ có nghiệm.
| $1\leq m\leq5$ | |
| $-4\leq m\leq0$ | |
| $0\leq m\leq4$ | |
| $m\leq 5$ |
Để phương trình \((m-1)x^2+3mx+m^2-m-6=0\) có hai nghiệm trái dấu thì
| \(m\in(-\infty;-2)\cup(1;3)\) | |
| \(m\in(-\infty;-2]\cup[1;3]\) | |
| \(m\in(-2;1)\cup(3;+\infty)\) | |
| \(m\in[-2;1]\cup[3;+\infty)\) |
Cho phương trình \(\log_2^2(2x)-(m+2)\log_2x+m-2=0\) (\(m\) là tham số thực). Tập hợp tất cả các giá trị của \(m\) để phương trình đã cho có hai nghiệm phân biệt thuộc đoạn \([1;2]\) là
| \(\left(1;2\right)\) | |
| \(\left[1;2\right]\) | |
| \(\left[1;2\right)\) | |
| \(\left[2;+\infty\right)\) |
Với giá trị nào của \(m\) thì phương trình \((m-3)x^2+(m+3)x-(m+1)=0\) có hai nghiệm phân biệt?
| \(m\in\left(-\infty;-\dfrac{3}{5}\right)\cup(1;+\infty)\) | |
| \(m\in\left(-\infty;-\dfrac{3}{5}\right)\cup(1;3)\cup(3;+\infty)\) | |
| \(m\in\left(-\dfrac{3}{5};1\right)\) | |
| \(m\in\left(-\dfrac{3}{5};+\infty\right)\) |
Để phương trình \(\left(m^2-4\right)x^2+5x+m=0\) có hai nghiệm trái dấu thì
| \(m\in(\infty;-2]\cup[0;2]\) | |
| \(m\in(-\infty;-2)\cup(0;2)\) | |
| \(m\in(-2;0)\cup(2;+\infty)\) | |
| \(m\in(-2;2)\) |
Điều kiện cần và đủ để phương trình \(mx^2+2(m+1)x+m=0\) có hai nghiệm phân biệt là
| \(m\neq0\) và \(m>-\dfrac{1}{2}\) | |
| \(m>\dfrac{1}{2}\) | |
| \(m>-\dfrac{1}{2}\) | |
| \(m>0\) |
Có bao nhiêu giá trị nguyên của tham số \(m\in[-7;7]\) để phương trình \(mx^2-2(m+2)x+m-1=0\) có hai nghiệm phân biệt?
| \(14\) | |
| \(8\) | |
| \(7\) | |
| \(15\) |
Biết \(\displaystyle\int\limits_1^2{\dfrac{\mathrm{\,d}x}{4x^2-4x+1}}=\dfrac{1}{a}+\dfrac{1}{b}\) thì \(a,\,b\) là nghiệm của phương trình nào sau đây?
| \(x^2-5x+6=0\) | |
| \(x^2+4x-12=0\) | |
| \(2x^2-x-1=0\) | |
| \(x^2-9=0\) |
Phương trình \((m-1)x^2+3x-1=0\) có nghiệm khi và chỉ khi
| \(m\geq-\dfrac{5}{4}\) | |
| \(m>-\dfrac{5}{4}\) | |
| \(m=-\dfrac{5}{4}\) | |
| \(m\geq-\dfrac{5}{4}\) và \(m\neq1\) |
Tìm tất cả giá trị của tham số \(m\) để phương trình \(x^2+2mx-m-1=0\) có 2 nghiệm phân biệt \(x_1,\,x_2\) sao cho \(x_1^2+x_2^2=2\).
| \(\left[\begin{array}{l}m=-\dfrac{1}{2}\\ m=0\end{array}\right.\) | |
| \(m=0\) | |
| \(m=-\dfrac{1}{2}\) | |
| \(\left[\begin{array}{l}m=\dfrac{1}{2}\\ m=0\end{array}\right.\) |
Tập hợp các giá trị của \(m\) để phương trình \(x^2+mx-m+1=0\) có hai nghiệm trái dấu là
| \((1;10)\) | |
| \([1;+\infty)\) | |
| \((1;+\infty)\) | |
| \(\left(-2+\sqrt{8};+\infty\right)\) |
Nếu phương trình \(x^2-2mx+2+m=0\) có một nghiệm \(x=2\) thì
| \(m=1\) | |
| \(m=-1\) | |
| \(m=2\) | |
| \(m=-2\) |
Phương trình $3^{2x}-(m+1)3^x+m=0$ có đúng một nghiệm khi
| $m=0$ | |
| $m>0$ | |
| $m>0$, $m\neq1$ | |
| $m=1$ hoặc $m\leq0$ |
Có bao nhiêu giá trị nguyên của tham số $m\in(-10;100)$ để tồn tại các số thực dương $a,\,b,\,x,\,y$ thỏa mãn $a\neq1$, $b\neq1$ và $a^{2x}=b^y=(ab)^{x+my}$?
| $0$ | |
| $100$ | |
| $99$ | |
| $98$ |
Cho hàm số $f(x)=ax^3+bx^2+cx+d$ ($a\neq0$) có đồ thị là đường cong trong hình bên.
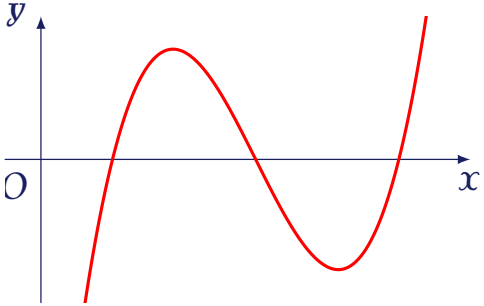
Số các giá trị nguyên của tham số $m\in(-2019;2023]$ để phương trình $4^{f(x)}-(m-1)2^{f(x)+1}+2m-3=0$ có đúng ba nghiệm là
| $2020$ | |
| $2019$ | |
| $2021$ | |
| $2022$ |
