Cho hàm số $y=f(x)=x^3-3x^2+12$. Tìm $x$ để $f'(x)< 0$.

	$x\in(-2;0)$
	$x\in(-\infty;-2)\cup(0;+\infty)$
	$x\in(0;2)$
	$x\in(-\infty;0)\cup(2;+\infty)$

Tìm tập xác định của hàm số $y=\sqrt{\dfrac{x^2+4x+5}{2x^2+3x+1}}$.

	$\left(-\infty;-1\right]\cup\left[-\dfrac{1}{2};+\infty\right)$
	$\left[-1;-\dfrac{1}{2}\right]$
	$\left(-\infty;-1\right)\cup\left(-\dfrac{1}{2};+\infty\right)$
	$\left(-1;-\dfrac{1}{2}\right)$

Tìm tập xác định \(\mathscr{D}\) của hàm số $$y=\dfrac{3-x}{\sqrt{4-3x-x^2}}$$

	\(\mathscr{D}=\mathbb{R}\setminus\{-4;1\}\)
	\(\mathscr{D}=[-4;1]\)
	\(\mathscr{D}=(-4;1)\)
	\(\mathscr{D}=(-\infty;4)\cup(1;+\infty)\)

Tìm tập xác định \(\mathscr{D}\) của hàm số $$y=\sqrt{2x^2-5x+2}$$

	\(\mathscr{D}=\left(-\infty;\dfrac{1}{2}\right]\)
	\(\mathscr{D}=\left[2;+\infty\right)\)
	\(\mathscr{D}=\left(-\infty;\dfrac{1}{2}\right]\cup[2;+\infty)\)
	\(\mathscr{D}=\left[\dfrac{1}{2};2\right]\)

Tìm tập xác định \(\mathscr{D}\) của hàm số \(y=\log_3\left(x^2-x-2\right)\).

	\(\mathscr{D}=(-1;2)\)
	\(\mathscr{D}=(-\infty;-1)\cup(2;+\infty)\)
	\(\mathscr{D}=(2;+\infty)\)
	\(\mathscr{D}=(-\infty;-1]\cup[3;+\infty)\)

Tìm tập xác định \(\mathscr{D}\) của hàm số \(y=\log_2\left(3x-x^2\right)\).

	\(\mathscr{D}=(0;+\infty)\)
	\(\mathscr{D}=(0;3)\)
	\(\mathscr{D}=[0;3]\)
	\(\mathscr{D}=\mathbb{R}\)

Tìm tập xác định \(\mathscr{D}\) của hàm số \(y=\log_2\left(3-2x-x^2\right)\).

	\(\mathscr{D}=(1;3)\)
	\(\mathscr{D}=(-1;3)\)
	\(\mathscr{D}=(-3;1)\)
	\(\mathscr{D}=(-\infty;-3)\cup(1;+\infty)\)

Tìm tập xác định \(\mathscr{D}\) của hàm số \(y=\log_2\left(x^2-2x-3\right)\).

	\(\mathscr{D}=[-1;3]\)
	\(\mathscr{D}=(-1;3)\)
	\(\mathscr{D}=(-\infty;-1]\cup[3;+\infty)\)
	\(\mathscr{D}=(-\infty;-1)\cup(3;+\infty)\)

Tập xác định của hàm số \(y=\log\left(x^2-1\right)\) là

	\((-\infty;-1)\cup(1;+\infty)\)
	\((-\infty;1)\)
	\((1;+\infty)\)
	\((-1;1)\)

Tìm tập xác định \(\mathscr{D}\) của hàm số \(y=\ln\left(x^2-2x+1\right)\).

	\(\mathscr{D}=\Bbb{R}\)
	\(\mathscr{D}=(1;+\infty)\)
	\(\mathscr{D}=\varnothing\)
	\(\mathscr{D}=\Bbb{R}\setminus\{1\}\)

Tập xác định của hàm số \(y=\left(x^2-4x\right)^{\mathrm{e}}\) là

	\(\Bbb{R}\)
	\(\Bbb{R}\setminus\{0;4\}\)
	\((-\infty;0)\cup(4;+\infty)\)
	\((0;4)\)

Tập xác định của hàm số \(y=\left(x^2-3x-4\right)^{\tfrac{1}{3}}\) là

	\((-\infty;-1)\cup(4;+\infty)\)
	\(\Bbb{R}\setminus\{-1;4\}\)
	\((-1;4)\)
	\(\Bbb{R}\)

Tập xác định của hàm số \(y=\left(x^2-5x+6\right)^{-\tfrac{1}{3}}\) là

	\((-\infty;2)\cup(3;+\infty)\)
	\(\Bbb{R}\setminus\{2;3\}\)
	\((2;3)\)
	\(\Bbb{R}\)

Tập xác định của hàm số \(y=\left(x^2-x+1\right)^{\pi}\) là

	\(\Bbb{R}\setminus\{1\}\)
	\(\Bbb{R}\)
	\(\varnothing\)
	\((-\infty;-1)\cup(1;+\infty)\)

Tập xác định của hàm số \(y=\left(x^2-3x+2\right)^{\pi}\) là

	\(\Bbb{R}\setminus\{1;2\}\)
	\((1;2)\)
	\((-\infty;1]\cup[2;+\infty)\)
	\((-\infty;1)\cup(2;+\infty)\)

Tìm tập xác định của hàm số \(y=\sqrt{2x^2-5x+2}\).

	\(\left(-\infty;\dfrac{1}{2}\right]\)
	\(\left[\dfrac{1}{2};2\right]\)
	\(\left(-\infty;\dfrac{1}{2}\right]\cup[2;+\infty)\)
	\([2;+\infty)\)

Cho hàm số $y=\dfrac{ax+b}{cx+d}$ có đồ thị là đường cong trong hình vẽ bên.

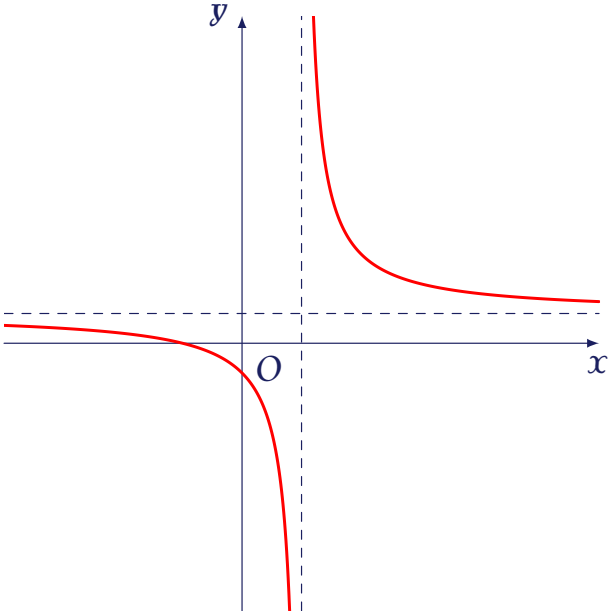
Kết luận nào sau đây đúng?

	$ad>0$, $bc< 0$
	$ad< 0$, $bc>0$
	$ad< 0$, $bc< 0$
	$ad>0$, $bc>0$

Cho hàm số $y=ax^2+bx+c$ có đồ thị như hình bên. Khẳng định nào sau đây là đúng?

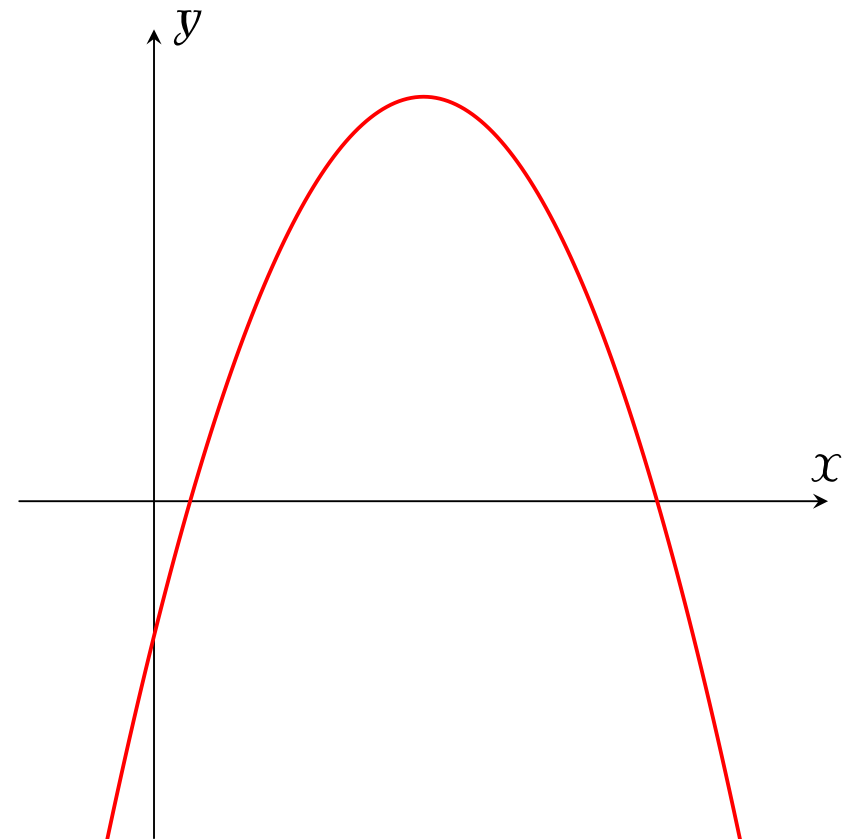
	$a>0,\,b>0,\,c<0$
	$a>0,\,b<0,\,c>0$
	$a<0,\,b>0,\,c<0$
	$a<0,\,b>0,\,c>0$

Cho hàm số $y=ax^2+bx+c$ có đồ thị như hình bên. Khẳng định nào sau đây là đúng?

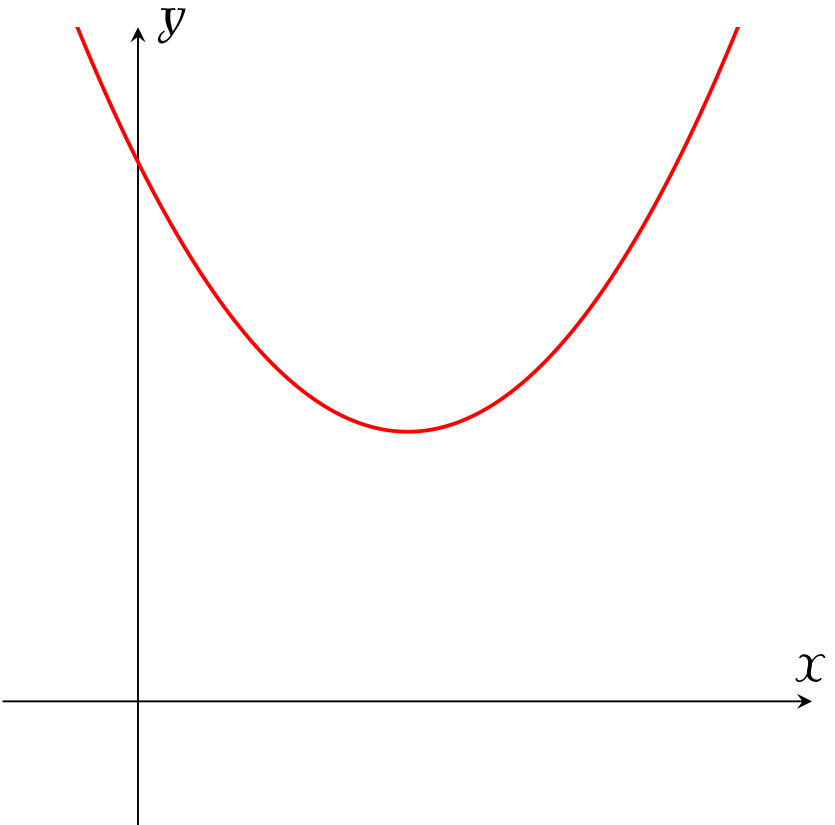
	$a>0,\,b<0,\,c<0$
	$a>0,\,b<0,\,c>0$
	$a>0,\,b>0,\,c>0$
	$a<0,\,b<0,\,c>0$

Hàm số $y=\left(3-x\right)\left(x+2\right)^2\left(x-2\right)^3$ nhận giá trị dương trên khoảng nào dưới đây?

	$\left(-2;2\right)$
	$\left(3;+\infty\right)$
	$\left(2;3\right)$
	$\left(-\infty;-2\right)$