Cho tứ diện $SABC$ có hai điểm $M$, $N$ lần lượt thuộc hai cạnh $SA$, $SB$ và $O$ là điểm nằm trong tam giác $ABC$. Hãy tìm
- Giao điểm của đường thẳng $AB$ và $(SOC)$.
- Giao điểm của đường thẳng $MN$ và $(SOC)$.
- Giao điểm của đường thẳng $SO$ và $(CMN)$.
Cho tứ diện $SABC$ có $M$ là điểm nằm trên tia đối của tia $SA$, $O$ là điểm thuộc miền trong của tam giác $ABC$. Hãy tìm
- Giao điểm của đường thẳng $BC$ và $(SOA)$.
- Giao điểm của đường thẳng $MO$ và $(SBC)$.
Cho hình chóp $S.ABCD$ với $ABCD$ là hình bình hành. Gọi $M$ là điểm lấy trên cạnh $SB$, $N$ là điểm thuộc miền trong của tam giác $SCD$. Hãy tìm giao điểm của
- Đường thẳng $MN$ và $(ABCD)$.
- Đường thẳng $SC$ và $(MAN)$.
- Đường thẳng $SD$ và $(MAN)$.
- Đường thẳng $SA$ và $(CMN)$.
Cho hình chóp $S.ABC$. Trên cạnh $SA$ lấy $M$ sao cho $SA=3SM$, trên cạnh $SC$ lấy điểm $N$ sao cho $SC=2SN$. Điểm $P$ thuộc cạnh $AB$. Hãy tìm
- Giao điểm của đường thẳng $MN$ và $(ABC)$.
- Giao điểm của đường thẳng $BC$ và $(MNP)$.
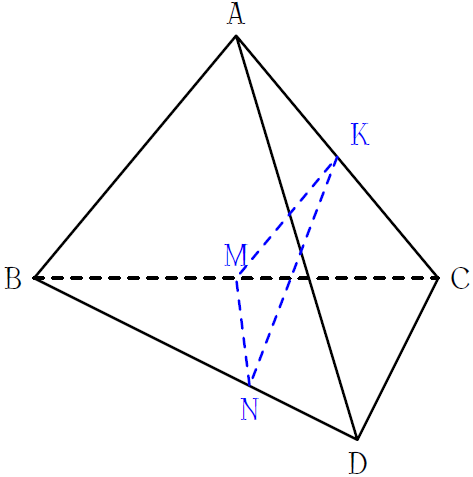
Cho tứ diện \(ABCD\). Gọi \(M,\,K\) lần lượt là trung điểm của \(BC\) và \(AC\), \(N\) là điểm trên cạnh \(BD\) sao cho \(BN=2ND\). Giao điểm của \(MN\) và \((ACD)\) là
| Giao điểm của \(MN\) với \(AD\) | |
| Giao điểm của \(MN\) với \(KD\) | |
| Giao điểm của \(MN\) với \(CD\) | |
| Không có |
Cho hình chóp $S.ABCD$ với đáy là hình bình hành tâm $O$. Gọi $G$ là trọng tâm của tam giác $SAB$. Hãy tìm
- Giao tuyến của $(SGC)$ và $(ABCD)$.
- Giao điểm của đường thẳng $AD$ và $(SGC)$.
- Giao điểm của đường thẳng $SO$ và $(GCD)$.
- Giao điểm của đường thẳng $SD$ và $(BCG)$.
Cho tứ diện $ABCD$. Gọi $M$ là điểm nằm trong tam giác $ABC$, $N$ là điểm nằm trong tam giác $ACD$. Tìm giao tuyến của các cặp mặt phẳng sau đây:
- $(CDM)$ và $(ABD)$.
- $(BCN)$ và $(ABD)$.
- $(CMN)$ và $(BCD)$.
Cho tứ diện $ABCD$ có $M$ nằm trên cạnh $AB$, $N$ nằm trên cạnh $AD$ thỏa $MB=2MA$, $AN=2ND$. Gọi $P$ là điểm thuộc miền trong của tam giác $BCD$. Tìm giao tuyến giữa
- $(CMN)$ và $(BCD)$.
- $(MNP)$ và $(CAD)$.
- $(MNP)$ và $(ABC)$.
Cho hình chóp $S.ABC$. Trên cạnh $SA$, $SC$ lấy $M$, $N$ sao cho $MN$ không song song $AC$. Gọi $O$ là điểm nằm miền trong của tam giác $ABC$. Tìm giao tuyến của
- $(MNO)$ và $(ABC)$.
- $(MNO)$ và $(SAB)$.
- $(SMO)$ và $(SBC)$.
- $(ONC)$ và $(SAB)$.
Cho tứ diện \(ABCD\). Gọi \(M,\,N\) lần lượt là trung điểm của các cạnh \(AD\) và \(BC\); \(G\) là trọng tâm tam giác \(BCD\).
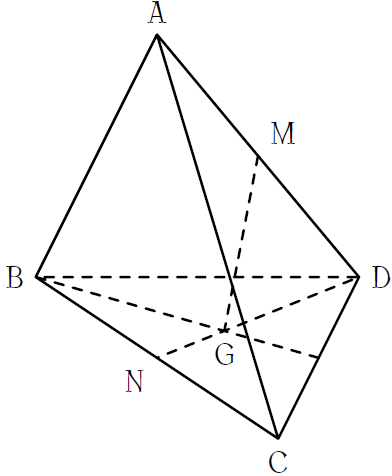
Khi ấy giao điểm của đường thẳng \(MG\) và mặt phẳng \((ABC)\) là
| Điểm \(C\) | |
| Điểm \(N\) | |
| Giao điểm của đường thẳng \(MG\) và đường thẳng \(BC\) | |
| Giao điểm của đường thẳng \(MG\) và đường thẳng \(AN\) |
Trong không gian $Oxyz$, xét mặt phẳng $(P)$ đi qua điểm $A(2;1;3)$ đồng thời cắt các tia $Ox$, $Oy$, $Oz$ lần lượt tại $M,\,N,\,P$ sao cho tứ diện $OMNP$ có thể tích nhỏ nhất. Giao điểm của đường thẳng $d\colon\begin{cases} x=2+t\\ y=1-t\\ z=4+t \end{cases}$ với $(P)$ có tọa độ là
| $(4;-1;6)$ | |
| $(4;6;1)$ | |
| $(-4;6;-1)$ | |
| $(4;1;6)$ |
Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác vuông tại $A$, $\widehat{ABC}=30^\circ$. Tam giác $SBC$ là tam giác đều cạnh $a$ và nằm trong mặt phẳng vuông góc với đáy. Thể tích khối chóp $S.ABC$ là
| $\dfrac{3a^3}{16}$ | |
| $\dfrac{a^3}{16}$ | |
| $\dfrac{a^3\sqrt{3}}{16}$ | |
| $\dfrac{3\sqrt{3}a^3}{16}$ |
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình bình hành và có thể tích bằng $1$. Trên cạnh $SC$ lấy điểm $E$ sao cho $SE=2EC$. Tính thể tích $V$ của khối tứ diện $SEBD$.
| $V=\dfrac{1}{12}$ | |
| $V=\dfrac{1}{3}$ | |
| $V=\dfrac{1}{6}$ | |
| $V=\dfrac{2}{3}$ |
Cho khối tứ diện $ABCD$. Hai điểm $M,\,N$ lần lượt là trung điểm của $BC$ và $BD$. Mặt phẳng $(AMN)$ chia khối tứ diện $ABCD$ thành
| Một khối tứ diện và một khối chóp tứ giác | |
| Hai khối chóp tứ giác | |
| Hai khối tứ diện | |
| Hai khối tứ diện và một khối chóp tứ giác |
Cho hình chóp $S.ABC$ có đáy là tam giác đều cạnh $a$. Hình chiếu của điểm $S$ trên mặt phẳng $(ABC)$ là điểm $H$ trên cạnh $AC$ thỏa mãn $AH=\dfrac{2}{3}AC$. Đường thẳng $SC$ tạo với mặt phẳng $(ABC)$ một góc bằng $60^\circ$. Thể tích của khối chóp $S.ABC$ bằng
| $\dfrac{a^3\sqrt{3}}{12}$ | |
| $\dfrac{a^3}{12}$ | |
| $\dfrac{a^3}{9}$ | |
| $\dfrac{a^3\sqrt{2}}{9}$ |
Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác vuông tại $A$, $AB=a$, $AC=2a$, $SA$ vuông góc với mặt phẳng đáy và $SB$ tạo với mặt đáy một góc $60^\circ$. Gọi $M,\,N$ lần lượt là trung điểm của $SB$ và $BC$. Thể tích khối chóp $A.SCNM$ bằng
| $\dfrac{\sqrt{3}}{4}a^3$ | |
| $\dfrac{\sqrt{3}}{2}a^3$ | |
| $\dfrac{3\sqrt{3}}{4}a^3$ | |
| $\dfrac{3\sqrt{3}}{2}a^3$ |
Nếu khối lăng trụ $ABC.A'B'C'$ có thể tích $V$ thì khối chóp $A'.ABC$ có thể tích bằng
| $\dfrac{V}{3}$ | |
| $V$ | |
| $\dfrac{2V}{3}$ | |
| $3V$ |
Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác đều cạnh $a$. Hình chiếu vuông góc của $S$ trên đáy là điểm $H$ trên cạnh $AC$ sao cho $AH=\dfrac{2}{3}AC$; mặt phẳng $(SBC)$ tạo với đáy một góc $60^{\circ}$. Thể tích khối chóp $S.ABC$ là
| $\dfrac{a^3\sqrt{3}}{12}$ | |
| $\dfrac{a^3\sqrt{3}}{48}$ | |
| $\dfrac{a^3\sqrt{3}}{36}$ | |
| $\dfrac{a^3\sqrt{3}}{24}$ |
Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác đều cạnh $a$, cạnh bên $SA=a$ và vuông góc với mặt đáy. Góc giữa đường thẳng $SC$ và mặt phẳng $(ABC)$ có số đo
| $45^\circ$ | |
| $90^\circ$ | |
| $30^\circ$ | |
| $60^\circ$ |
Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác đều cạnh $a$, cạnh bên $SA=a\sqrt{3}$ và vuông góc với mặt đáy. Góc giữa đường thẳng $SB$ và mặt phẳng $(ABC)$ có số đo
| $60^\circ$ | |
| $90^\circ$ | |
| $30^\circ$ | |
| $45^\circ$ |
