Hình lập phương có số đỉnh, số cạnh và số mặt tương ứng là
| $12;8;6$ | |
| $8;6;12$ | |
| $6;12;8$ | |
| $8;12;6$ |
Khối đa diện đều loại $\{4,3\}$ có bao nhiêu mặt?
| $4$ | |
| $6$ | |
| $8$ | |
| $12$ |
Khối lập phương là khối đa diện loại
| $\{5,3\}$ | |
| $\{3,4\}$ | |
| $\{4,3\}$ | |
| $\{3,5\}$ |
Cho khối lập phương có cạnh bằng $2a$. Thể tích của khối lập phương đã cho bằng
| $\dfrac{8}{3}a^3$ | |
| $8a^3$ | |
| $4a^3$ | |
| $\dfrac{4}{3}a^3$ |
Thể tích của khối lập phương cạnh $4a$ bằng
| $16a^3$ | |
| $36a^3$ | |
| $27a^3$ | |
| $64a^3$ |
Khối đa diện đều như hình bên là khối đa diện nào sau đây?
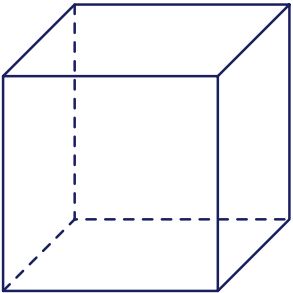
| Khối lập phương | |
| Khối tứ diện đều | |
| Khối mười hai mặt đều | |
| Khối bát diện đều |
Thể tích khối lăng trụ có chiều cao là $h$ và diện tích đáy là $B$ bằng
| $Bh$ | |
| $\dfrac{1}{3}Bh$ | |
| $3Bh$ | |
| $\dfrac{4}{3}Bh$ |
Cho khối lập phương có cạnh bằng $2$. Thể tích của khối lập phương đã cho bằng
| $6$ | |
| $8$ | |
| $\dfrac{8}{3}$ | |
| $4$ |
Khối đa diện đều nào sau đây có các mặt không phải là tam giác đều?
| Hai mươi mặt đều | |
| Bát diện đều | |
| Tứ diện đều | |
| Mười hai mặt đều |
Trong một khối đa diện, mệnh đề nào sau đây đúng?
| Hai cạnh bất kì có ít nhất một điểm chung | |
| Mỗi cạnh là cạnh chung của đúng $2$ mặt | |
| Mỗi đỉnh là đỉnh chung của ít nhất $2$ mặt | |
| Hai mặt bất kì có ít nhất một điểm chung |
Cho hình lập phương có tổng diện tích các mặt bằng $12a^2$. Tính theo $a$ thể tích khối lập phương đó.
| $\sqrt{2}a^3$ | |
| $a^3$ | |
| $2\sqrt{2}a^3$ | |
| $\dfrac{a^3}{3}$ |
Thể tích của khối lập phương cạnh $4a$ bằng
| $16a^3$ | |
| $36a^3$ | |
| $27a^3$ | |
| $64a^3$ |
Hình nhị thập diện đều có số đỉnh, số cạnh và số mặt tương ứng là
| $12;20;30$ | |
| $12;30;20$ | |
| $20;12;30$ | |
| $30;20;12$ |
Số cạnh của một hình nhị thập diện đều là
| $30$ | |
| $15$ | |
| $12$ | |
| $20$ |
Số đỉnh của một hình nhị thập diện đều là
| $20$ | |
| $8$ | |
| $10$ | |
| $12$ |
Hình thập nhị diện đều có số đỉnh, số cạnh và số mặt tương ứng là
| $12;30;20$ | |
| $20;30;12$ | |
| $20;12;30$ | |
| $30;20;12$ |
