Đồ thị hàm số nào sau đây nhận trục $Oy$ làm trục đối xứng?
| $y=x^3-|x|$ | |
| $y=x^2-|x|$ | |
| $y=x^2-x$ | |
| $y=x^3-x$ |
Xét tính chẵn lẻ của hai hàm số $f(x)=|x+2|-|x-2|$ và $g(x)=-|x|$.
| $f(x)$ chẵn, $g(x)$ chẵn | |
| $f(x)$ lẻ, $g(x)$ chẵn | |
| $f(x)$ lẻ, $g(x)$ lẻ | |
| $f(x)$ chẵn, $g(x)$ lẻ |
Hàm số nào sau đây là hàm số lẻ?
| $y=2x$ | |
| $y=x^3+x^2$ | |
| $y=x^3+1$ | |
| $y=|x|+1$ |
Chọn mệnh đề đúng trong các mệnh đề sau:
| Đồ thị của hàm số chẵn nhận trục tung làm trục đối xứng | |
| Đồ thị của hàm số lẻ nhận trục tung làm trục đối xứng | |
| Đồ thị của hàm số lẻ nhận trục hoành làm trục đối xứng | |
| Đồ thị của hàm số chẵn nhận trục hoành làm trục đối xứng |
Hàm số nào sau đây có tập xác định là $\mathbb{R}$?
| $y=\dfrac{x}{x^2-1}$ | |
| $y=3x^3-2|x|-3$ | |
| $y=3x^3-2\sqrt{x}-3$ | |
| $y=\dfrac{\sqrt{x}}{x^2+1}$ |
Hàm số nào sau đây có đồ thị đối xứng qua trục tung?
| $y=\left|x+1\right|+\left|x-1\right|$ | |
| $y=\left|x+3\right|+\left|x-2\right|$ | |
| $y=2x^3-3x$ | |
| $y=2x^4-3x^2+x$ |
Cho ba hàm số $f\left(x\right)=-2x^3+3x$, $g\left(x\right)=x^{2019}+2019$ và $h\left(x\right)=x^2-|x|$. Mệnh đề nào sau đây đúng?
| $f\left(x\right)$ chẵn, $g\left(x\right)$ lẻ, $h\left(x\right)$ không chẵn không lẻ | |
| $g\left(x\right)$ chẵn, $h\left(x\right)$ lẻ, $f\left(x\right)$ không chẵn không lẻ | |
| $h\left(x\right)$ chẵn, $f\left(x\right)$ lẻ, $g\left(x\right)$ không chẵn không lẻ | |
| $f\left(x\right)$ chẵn, $h\left(x\right)$ lẻ, $g\left(x\right)$ không chẵn không lẻ |
Cho hàm số \(y=\tan x\) có đồ thị như hình vẽ:
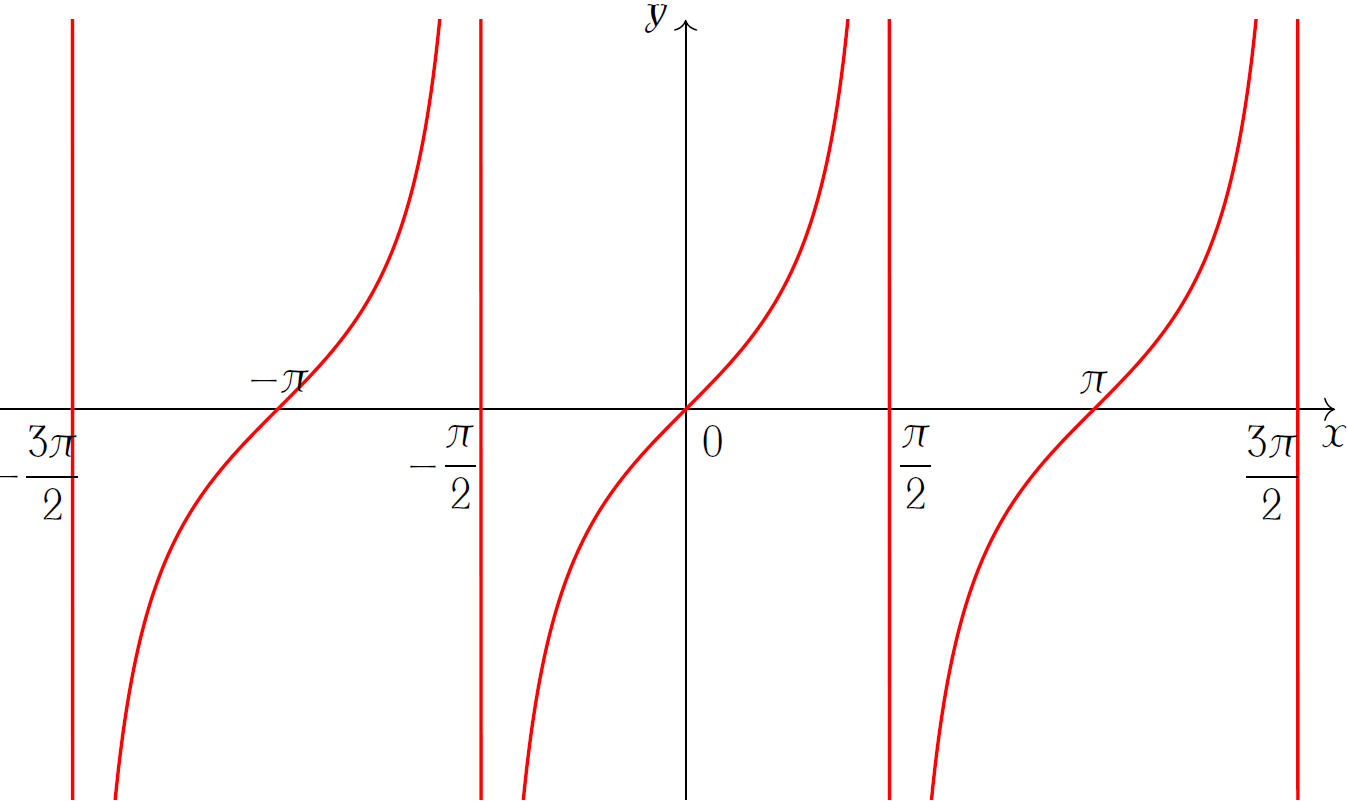
Khẳng định nào sau đây sai?
| Hàm số đồng biến trên \(\left(-\dfrac{\pi}{2};0\right)\) | |
| \(\tan x>0,\forall x\in\left(0;\dfrac{\pi}{2}\right)\) | |
| Đồ thị hàm số luôn cắt trục hoành tại một điểm | |
| Đồ thị hàm số nhận gốc tọa độ \(O\) làm tâm đối xứng nên hàm số \(y=\tan x\) là hàm số lẻ |
Cho hai hàm số \(f(x)=\dfrac{\cos2x}{1+\sin^23x}\) và \(g(x)=\dfrac{\left|\sin2x\right|-\cos3x}{2+\tan^2x}\). Chọn mệnh đề đúng trong các mệnh đề sau:
| \(f(x)\) là hàm số chẵn, \(g(x)\) là hàm số lẻ | |
| \(f(x)\) là hàm số lẻ, \(g(x)\) là hàm số chẵn | |
| \(f(x)\) và \(g(x)\) đều là hàm số chẵn | |
| \(f(x)\) và \(g(x)\) đều là hàm số lẻ |
Mệnh đề nào sau đây là sai?
| Đồ thị hàm số \(y=\left|\sin x\right|\) đối xứng qua gốc tọa độ \(O\) | |
| Đồ thị hàm số \(y=\cos x\) đối xứng qua trục \(Oy\) | |
| Đồ thị hàm số \(y=\left|\tan x\right|\) đối xứng qua trục \(Oy\) | |
| Đồ thị hàm số \(y=\tan x\) đối xứng qua gốc tọa độ \(O\) |
Hàm số nào sau đây có đồ thị đối xứng qua gốc tọa độ?
| \(y=\cot4x\) | |
| \(y=\dfrac{\sin x+1}{\cos x}\) | |
| \(y=\tan^2x\) | |
| \(y=\left|\cot x\right|\) |
Hàm số nào sau đây là hàm số chẵn?
| \(y=\left|\sin x\right|\) | |
| \(y=x^2\sin x\) | |
| \(y=\dfrac{x}{\cos x}\) | |
| \(y=x+\sin x\) |
Tìm tập xác định \(\mathscr{D}\) của hàm số \(y=\dfrac{1}{\sqrt{2-x}}+\ln|x-1|\).
| \(\mathscr{D}=(-\infty;2)\setminus\{1\}\) | |
| \(\mathscr{D}=(1;2)\) | |
| \(\mathscr{D}=[1;2)\) | |
| \(\mathscr{D}=(1;2]\) |
Tìm tất cả các giá trị thực của tham số $m$ để hàm số $y=\ln\big(x^2-2x+m+1\big)$ có tập xác định là $\mathbb{R}$.
| $m=0$ | |
| $m< -1$ hoặc $m>0$ | |
| $m>0$ | |
| $0< m< 3$ |
Tìm tập xác định của hàm số $y=\log_{2023}\big(3x-x^2\big)$.
| $\mathscr{D}=(0;+\infty)$ | |
| $\mathscr{D}=(-\infty;0)\cup(3;+\infty)$ | |
| $\mathscr{D}=\mathbb{R}$ | |
| $\mathscr{D}=(0;3)$ |
Tập xác định của hàm số $y=x^{\sqrt{2}-1}$ là
| $\big(-\infty;\sqrt{2}\big)$ | |
| $\mathbb{R}\setminus\{0\}$ | |
| $\mathbb{R}$ | |
| $(0;+\infty)$ |
Tập xác định của hàm số $y=\log_{\sqrt{3}}x$ là
| $[0;+\infty)$ | |
| $(0;+\infty)$ | |
| $(-\infty;0)$ | |
| $\mathbb{R}$ |
Tập xác định của hàm số $y=\log_{2022}(2x-1)$ là
| $[0;+\infty)$ | |
| $\left(\dfrac{1}{2};+\infty\right)$ | |
| $\left[\dfrac{1}{2};+\infty\right)$ | |
| $(0;+\infty)$ |
Có bao nhiêu giá trị nguyên của tham số $m$ để hàm số $y=\big|3x^4-4x^3-12x^2+m\big|$ có $7$ điểm cực trị?
| $4$ | |
| $6$ | |
| $3$ | |
| $5$ |
Có bao nhiêu giá trị nguyên của tham số a thuộc đoạn $[-10;10]$ để hàm số $$y=\big|-x^3+3(a+1)x^2-3a(a+2)x+a^2(a+3)\big|$$đồng biến trên khoảng $(0;1)$
| $21$ | |
| $10$ | |
| $8$ | |
| $2$ |
