Cho hàm số $y=\big(2x^2-1\big)^{\tfrac{1}{2}}$. Giá trị của hàm số đã cho tại điểm $x=2$ bằng
| $3$ | |
| $\sqrt{7}$ | |
| $\sqrt{3}$ | |
| $7$ |
Điểm nào sau đây thuộc đồ thị hàm số $y=2|x-1|+3|x|-2$?
| $A(2;6)$ | |
| $B(1;-1)$ | |
| $C(-2;-10)$ | |
| Cả ba điểm $A,\,B,\,C$ |
Điểm nào sau đây không thuộc đồ thị hàm số $y=\dfrac{\sqrt{x^2-4x+4}}{x}$?
| $A(2;0)$ | |
| $B\left(3;\dfrac{1}{3}\right)$ | |
| $C(1;-1)$ | |
| $D(-1;-3)$ |
Tính giá trị của hàm số $f(x)=x+1$ tại $x=2$.
| $0$ | |
| $3$ | |
| $2$ | |
| $-1$ |
Cho hàm số $f\left(x\right)=\left|-5x\right|$. Chọn mệnh đề sai?
| $f\left(-1\right)=5$ | |
| $f\left(2\right)=10$ | |
| $f\left(-2\right)=10$ | |
| $f\left(\dfrac{1}{5}\right)=-1$ |
Giới hạn \(\lim\limits_{x\to-\infty}\dfrac{\sqrt{x^2+1}-x}{5-2|x|}\) bằng
| \(-1\) | |
| \(0\) | |
| \(+\infty\) | |
| \(-\infty\) |
Giới hạn bên trái của hàm số \(f(x)=\dfrac{|2x+1|}{2x+1}\) tại \(x_0=-\dfrac{1}{2}\) bằng
| \(-1\) | |
| \(1\) | |
| \(-\dfrac{1}{2}\) | |
| Không tồn tại |
Giới hạn \(\lim\limits_{x\to3^-}\dfrac{x^2+2x-15}{|x-3|}\) bằng
| \(8\) | |
| \(-\infty\) | |
| \(-8\) | |
| Không tồn tại |
Quan sát lời giải sau, lỗi sai bắt đầu từ dòng nào?
\lim\limits_{x\to1^-}\dfrac{x^2-3x+2}{|x-1|}&=\lim\limits_{x\to1^-}\dfrac{x^2-3x+2}{x-1}\\
&=\lim\limits_{x\to1^-}\dfrac{(x-1)(x-2)}{x-1}\\
&=\lim\limits_{x\to1^-}(x-2)\\
&=1-2=-1.
\end{aligned}$$
| Dòng 1 | |
| Dòng 2 | |
| Dòng 3 | |
| Dòng 4 |
Tính giới hạn \(\lim\limits_{x\to-3}\left|\dfrac{-x^2-x+6}{x^2+3x}\right|\).
| \(\dfrac{1}{3}\) | |
| \(\dfrac{2}{3}\) | |
| \(\dfrac{5}{3}\) | |
| \(\dfrac{3}{5}\) |
Tính giới hạn \(\lim\limits_{x\to-\infty}\left(|x|^3+2x^2+3|x|\right)\).
| \(0\) | |
| \(+\infty\) | |
| \(1\) | |
| \(-\infty\) |
Tính giới hạn \(\lim\limits_{x\to2^-}\dfrac{|2-x|}{2x^2-5x+2}\).
| \(-\infty\) | |
| \(+\infty\) | |
| \(-\dfrac{1}{3}\) | |
| \(\dfrac{1}{3}\) |
Tính giới hạn \(\lim\limits_{x\to(-2)^+}\dfrac{\left|3x+6\right|}{x+2}\).
| \(-\infty\) | |
| \(3\) | |
| \(+\infty\) | |
| \(0\) |
Giới hạn \(\lim\limits_{x\to-1}\dfrac{|x-1|}{x^4+x-3}\) bằng
| \(-\dfrac{3}{2}\) | |
| \(\dfrac{2}{3}\) | |
| \(\dfrac{3}{2}\) | |
| \(-\dfrac{2}{3}\) |
Giá trị của giới hạn \(\lim\limits_{x\to\sqrt{3}}\left|x^2-4\right|\) là
| \(0\) | |
| \(1\) | |
| \(2\) | |
| \(3\) |
Biết đồ thị của hàm số $f(x)=ax^3+bx^2+cx+d$ có hai điểm cực trị là $A(1;1)$ và $B\left(2;\dfrac{4}{3}\right)$. Tính $f(-1)$.
| $12$ | |
| $7$ | |
| $\dfrac{31}{3}$ | |
| $\dfrac{16}{3}$ |
Có bao nhiêu giá trị nguyên của tham số $m$ để hàm số $y=\big|3x^4-4x^3-12x^2+m\big|$ có $7$ điểm cực trị?
| $4$ | |
| $6$ | |
| $3$ | |
| $5$ |
Có bao nhiêu giá trị nguyên của tham số a thuộc đoạn $[-10;10]$ để hàm số $$y=\big|-x^3+3(a+1)x^2-3a(a+2)x+a^2(a+3)\big|$$đồng biến trên khoảng $(0;1)$
| $21$ | |
| $10$ | |
| $8$ | |
| $2$ |
Có bao nhiêu giá trị nguyên của tham số $a\in(-10;+\infty)$ để hàm số $y=\big|x^3+(a+2)x+9-a^2\big|$ đồng biến trên khoảng $(0;1)$?
| $12$ | |
| $11$ | |
| $6$ | |
| $5$ |
Cho hàm số $f(x)$, trong đó $f(x)$ là một đa giác. Hàm số $f'(x)$ có đồ thị như hình vẽ bên.
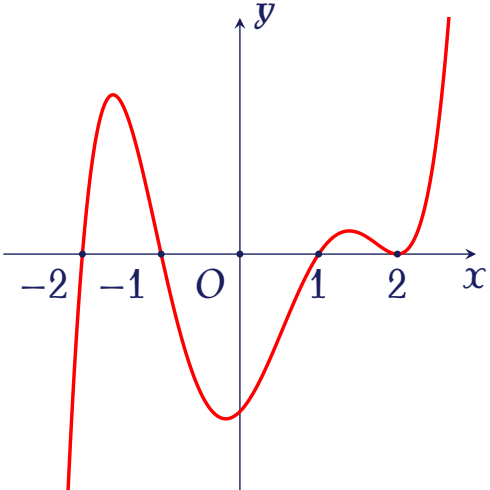
Hỏi có bao nhiêu giá trị nguyên $m$ thuộc $(-5;5)$ để hàm số $y=g(x)=f\big(x^2-2|x|+m\big)$ có $9$ điểm cực trị?
| $3$ | |
| $4$ | |
| $1$ | |
| $2$ |
