Điểm nào sau đây thuộc đồ thị hàm số $y=2|x-1|+3|x|-2$?
| $A(2;6)$ | |
| $B(1;-1)$ | |
| $C(-2;-10)$ | |
| Cả ba điểm $A,\,B,\,C$ |
Điểm nào sau đây không thuộc đồ thị hàm số $y=\dfrac{\sqrt{x^2-4x+4}}{x}$?
| $A(2;0)$ | |
| $B\left(3;\dfrac{1}{3}\right)$ | |
| $C(1;-1)$ | |
| $D(-1;-3)$ |
Hàm số nào dưới đây có bảng biến thiên như hình bên?
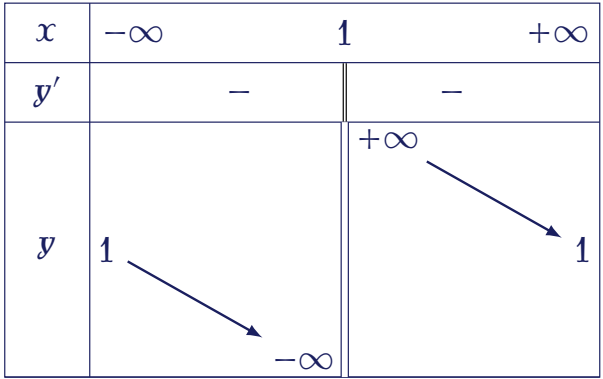
| $y=-x^3+3x+1$ | |
| $y=\dfrac{x-1}{x+1}$ | |
| $y=\dfrac{x+1}{x-1}$ | |
| $y=x^4-x^2+1$ |
Cho hàm số $f(x)=ax^4+bx^2+c$ ($a\neq0$) có đồ thị là đường cong trong hình bên.
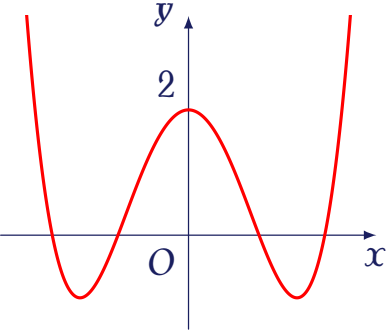
Số nghiệm của phương trình $f(x)-1=0$ là
| $2$ | |
| $1$ | |
| $4$ | |
| $3$ |
Hàm số nào sau đây có đồ thị như đường cong trong hình bên dưới?
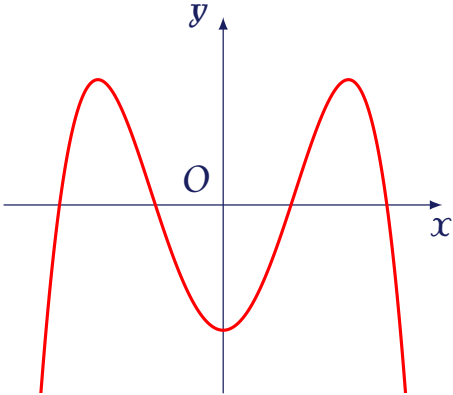
| $y=-x^4+3x^2-1$ | |
| $y=x^4-3x^2-1$ | |
| $y=x^3-x^2-1$ | |
| $y=-x^3+x^2-1$ |
Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình vẽ?
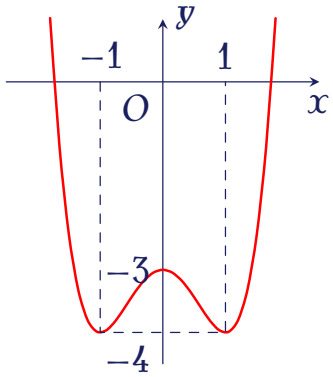
| $y=-x^4+2x^2-3$ | |
| $y=-x^3+3x$ | |
| $y=x^4-2x^2-3$ | |
| $y=x^3-3x-3$ |
Cho hàm số $y=ax^4+bx^2+c$ có đồ thị là đường cong trong hình bên.
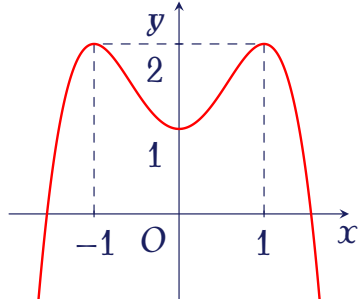
Điểm cực tiểu của đồ thị hàm số đã cho có tọa độ là
| $(-1;2)$ | |
| $(0;1)$ | |
| $(1;2)$ | |
| $(1;0)$ |
Đường cong trong hình vẽ sau là đồ thị của hàm số nào dưới đây?
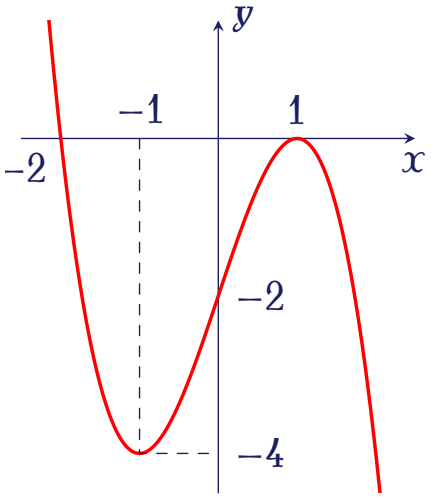
| $y=-x^3+3x-2$ | |
| $y=x^3-3x+2$ | |
| $y=x^4-3x^2-2$ | |
| $y=x^4-3x^2+2$ |
Cho hàm số $y=ax^4+bx^2+c$ có đồ thị như đường cong trong hình bên.
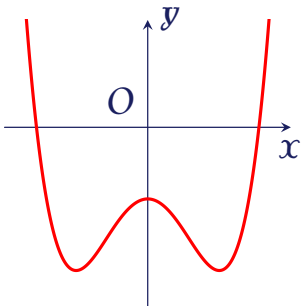
Số điểm cực trị của hàm số đã cho là
| $2$ | |
| $3$ | |
| $1$ | |
| $0$ |
Cho hàm số $f(x)=ax^4+bx^2+c$ có đồ thị là đường cong trong hình bên.
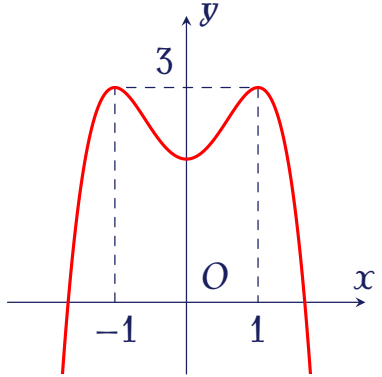
Số nghiệm thực của phương trình $f(x)=1$ là
| $1$ | |
| $2$ | |
| $4$ | |
| $3$ |
Cho hàm số $y=ax^4+bx^2+c$ có đồ thị như hình vẽ bên.
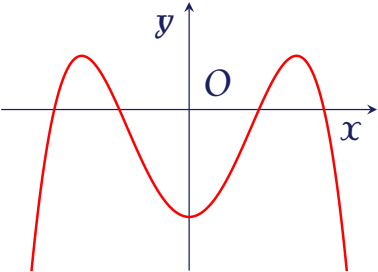
Mệnh đề nào dưới đây đúng?
| $a>0,\,b< 0,\,c< 0$ | |
| $a< 0,\,b< 0,\,c< 0$ | |
| $a< 0,\,b>0,\,c< 0$ | |
| $a>0,\,b< 0,\,c>0$ |
Cho hàm số $y=f(x)$ có đồ thị là đường cong trong hình bên.
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
| $(0;1)$ | |
| $(-\infty;0)$ | |
| $(0;+\infty)$ | |
| $(-1;1)$ |
Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên
| $y=-2x^4+4x^2-1$ | |
| $y=-x^2+3x-1$ | |
| $y=2x^4-4x^2-1$ | |
| $y=x^3-3x-1$ |
Cho hàm số $y=ax^4+bx^2+c$ ($a,\,b,\,c\in\mathbb{R})$ có đồ thị là đường cong trong hình bên.
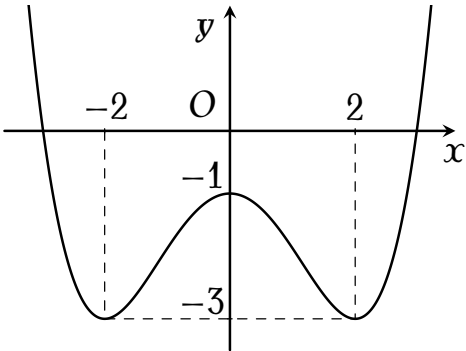
Giá trị cực đại của hàm số đã cho bằng
| $0$ | |
| $-1$ | |
| $-3$ | |
| $2$ |
Hàm số nào dưới đây có đồ thị như đường cong trong hình bên?
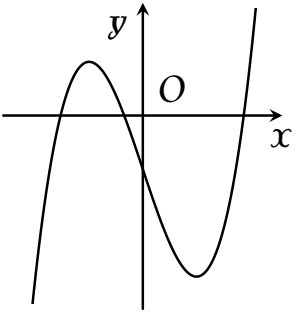
| $y=x^4-2x^2-1$ | |
| $y=\dfrac{x+1}{x-1}$ | |
| $y=x^3-3x-1$ | |
| $y=x^2+x-1$ |
Điểm nào dưới đây thuộc đồ thị của hàm số $y=x^4+x^2-2$?
| Điểm $P(-1;-1)$ | |
| Điểm $N(-1;-2)$ | |
| Điểm $M(-1;0)$ | |
| Điểm $Q(-1;1)$ |
Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên?
| $y=-x^4+2x^2-1$ | |
| $y=x^4-2x^2-1$ | |
| $y=x^3-3x^2-1$ | |
| $y=-x^3+3x^2-1$ |
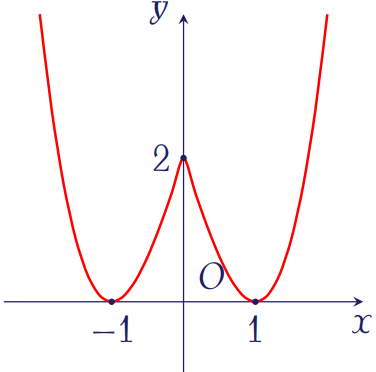
Đồ thị như hình trên là của hàm số nào sau đây?
| \(y=x^4-2x^2+2\) | |
| \(y=2\left(x^2-1\right)^2\) | |
| \(y=|x|^3-3|x|+2\) | |
| \(y=x^2-2|x|^2+2\) |
Đồ thị nào sau đây không thể là đồ thị hàm số \(y=ax^4+bx^2+c\) với \(a,\,b,\,c\) là các số thực và \(a\neq0\)?
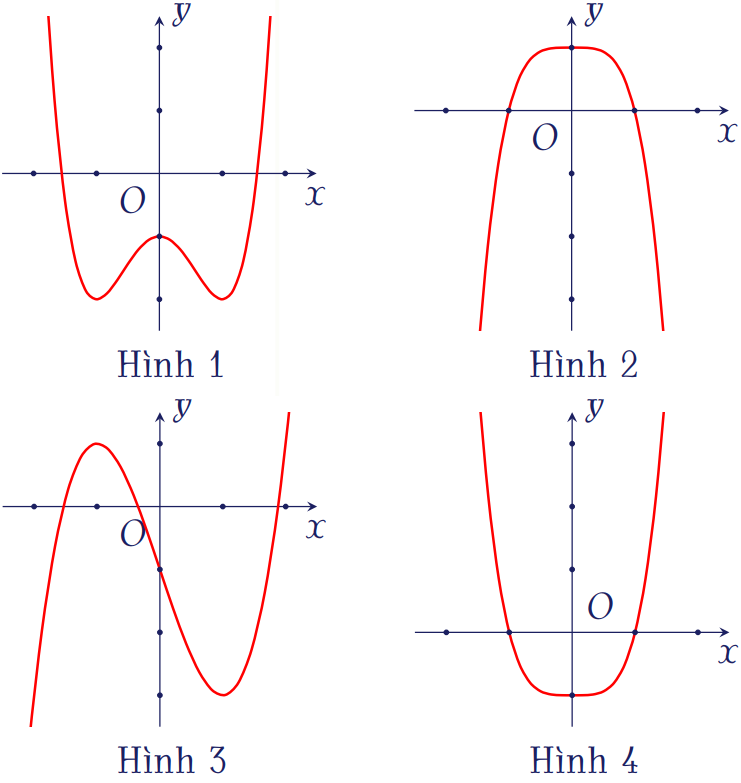
| Hình 1 | |
| Hình 2 | |
| Hình 3 | |
| Hình 4 |
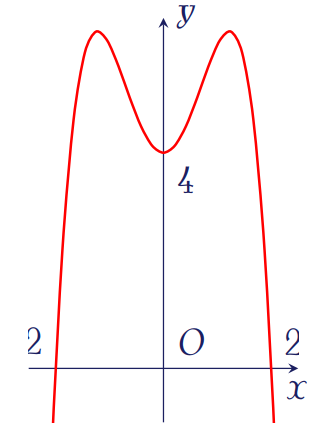
Đồ thị trong hình vẽ bên là của hàm số
| \(y=-x^2+x-4\) | |
| \(y=x^4-3x^2-4\) | |
| \(y=-x^3+2x^2+4\) | |
| \(y=-x^4+3x^2+4\) |
