Xác định parabol $\left(\mathscr{P}\right)\colon y=2x^2+bx+c$, biết rằng $\left(\mathscr{P}\right)$ có đỉnh $I(-1;-2)$.
| $y=2x^2-4x+4$ | |
| $y=2x^2-4x$ | |
| $y=2x^2-3x+4$ | |
| $y=2x^2+4x$ |
Hàm số nào sau đây đạt giá trị nhỏ nhất tại $x=\dfrac{3}{4}$?
| $y=4x^2-3x+1$ | |
| $y=-x^2+\dfrac{3}{2}x+1$ | |
| $y=-2x^2+3x+1$ | |
| $y=x^2-\dfrac{3}{2}x+1$ |
Tìm giá trị nhỏ nhất $m$ của hàm số $y=x^2-4x+5$.
| $m=0$ | |
| $m=-2$ | |
| $m=2$ | |
| $m=1$ |
Hàm số nào sau đây có đồ thị là parabol có đỉnh $I(-1;3)$?
| $y=2x^2-4x-3$ | |
| $y=2x^2-2x-1$ | |
| $y=2x^2+4x+5$ | |
| $y=2x^2+x+2$ |
Cho hàm số $y=ax^2+bx+c$ $(a\neq0)$ có đồ thị $\left(\mathscr{P}\right)$. Tọa độ đỉnh của $\left(\mathscr{P}\right)$ là
| $I\left(-\dfrac{b}{2a};\dfrac{\Delta}{4a}\right)$ | |
| $I\left(-\dfrac{b}{a};-\dfrac{\Delta}{4a}\right)$ | |
| $I\left(-\dfrac{b}{2a};-\dfrac{\Delta}{4a}\right)$ | |
| $I\left(\dfrac{b}{2a};\dfrac{\Delta}{4a}\right)$ |
Đỉnh của parabol $\left(P\right)\colon y=3x^2-2x+1$ là
| $I\left(-\dfrac{1}{3};\dfrac{2}{3}\right)$ | |
| $J\left(-\dfrac{1}{3};-\dfrac{2}{3}\right)$ | |
| $K\left(\dfrac{1}{3};-\dfrac{2}{3}\right)$ | |
| $L\left(\dfrac{1}{3};\dfrac{2}{3}\right)$ |
Parabol \(y=x^2-x+3\) có đỉnh là
| \(A\left(\dfrac{1}{2};\dfrac{11}{4}\right)\) | |
| \(x=\dfrac{1}{2}\) | |
| \(B\left(-\dfrac{1}{2};\dfrac{15}{4}\right)\) | |
| \(I(1;3)\) |
Hàm số nào dưới đây có bảng biến thiên như sau?
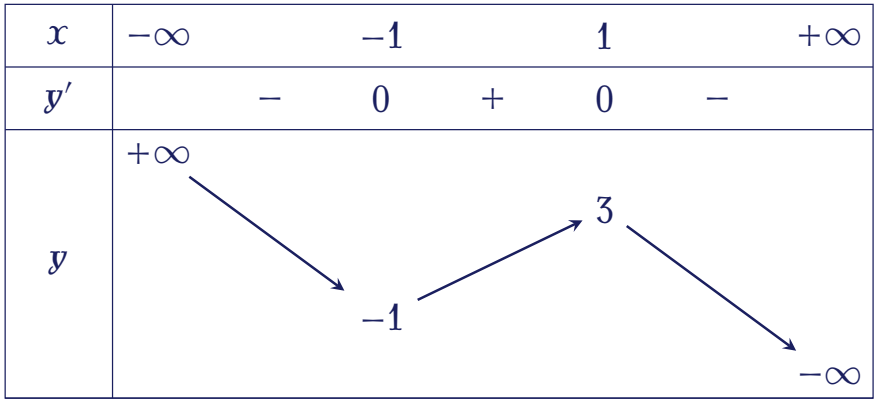
| $y=\dfrac{x+2}{x}$ | |
| $y=-x^3+3x+1$ | |
| $y=x^4-3x^2$ | |
| $y=-2x^2+1$ |
Trong các hàm số sau, hàm số nào không có cực trị?
| $y=x^2$ | |
| $y=\dfrac{x+2}{2x-1}$ | |
| $y=x^4+2x^2+2$ | |
| $y=-x^3-x^2$ |
Cho hàm số $y=x^2+4$. Khẳng định nào dưới đây đúng?
| $\displaystyle\displaystyle\int f(x)\mathrm{\,d}x=2x+C$ | |
| $\displaystyle\displaystyle\int f(x)\mathrm{\,d}x=x^2+4x+C$ | |
| $\displaystyle\displaystyle\int f(x)\mathrm{\,d}x=\dfrac{x^3}{3}+4x+C$ | |
| $\displaystyle\displaystyle\int f(x)\mathrm{\,d}x=x^3+4x+C$ |
Tính thể tích $V$ của khối tròn xoay khi cho diện tích hình phẳng giới hạn bởi đồ thị hàm số $y=2x-x^2$, trục $Ox$ quay quanh $Ox$.
| $V=\dfrac{8\pi}{15}$ | |
| $V=\dfrac{32\pi}{15}$ | |
| $V=\dfrac{4\pi}{3}$ | |
| $V=\dfrac{16\pi}{15}$ |
Tính diện tích $S$ của hình phẳng giới hạn bởi đồ thị hàm số $y=x^2-4x$, $Ox$ và $x=0,\,x=2$.
| $S=9$ | |
| $S=\dfrac{16}{3}$ | |
| $S=\dfrac{32}{3}$ | |
| $S=\dfrac{5}{3}$ |
Điện lượng truyền trong dây dẫn có phương trình $Q=t^2$. Tính cường độ dòng điện tức thời tại thời điểm $t_0=5$ (giây).
| $3$(A) | |
| $25$(A) | |
| $10$(A) | |
| $2$(A) |
Phương trình tiếp tuyến của đồ thị hàm số $y=\dfrac{1}{2}x^2-2x+1$ biết tiếp tuyến song song với đường thẳng $y=2x+3$ là
| $y=2x+5$ | |
| $y=3x+5$ | |
| $y=-2x+7$ | |
| $y=2x–7$ |
Tìm phương trình tiếp tuyến của đồ thị hàm số $y=f(x)=-3x^2+x+3$ $(\mathscr{P})$ tại điểm $M(1;1)$.
| $y=-5x+6$ | |
| $y=5x-6$ | |
| $y=-5x-6$ | |
| $y=5x+6$ |
Cho hai hàm số $f(x)=x^2+2$, $g(x)=\dfrac{1}{1-x}$. Tính $\dfrac{f’(1)}{g’(0)}$.
| $0$ | |
| $-2$ | |
| $2$ | |
| $1$ |
Số gia của hàm số $y=f(x)=x^2+2x-3$ ứng với số gia $\Delta x$ của đối số tại $x_0=1$ là
| $\Delta y=\Delta^2x-4\Delta x$ | |
| $\Delta y=\Delta^2x+2\Delta x$ | |
| $\Delta y=4\Delta x$ | |
| $\Delta y=\Delta^2x+4\Delta x$ |
Cho hàm số $f(x)=3x^4+ax^3+bx^2+cx+d$ $(a,\,b,\,c,\,d\in\mathbb{R})$ có ba điểm cực trị là $-2,\,-1$ và $1$. Gọi $y=g(x)$ là hàm số bậc hai có đồ thị đi qua ba điểm cực trị của đồ thị hàm số $y=f(x)$. Diện tích hình phẳng giới hạn bởi hai đường $y=f(x)$ và $y=g(x)$ bằng
| $\dfrac{500}{81}$ | |
| $\dfrac{36}{5}$ | |
| $\dfrac{2932}{405}$ | |
| $\dfrac{2948}{405}$ |
Hàm số nào dưới đây có đồ thị như đường cong trong hình bên?
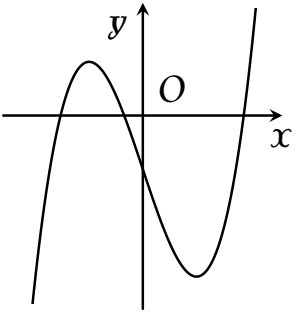
| $y=x^4-2x^2-1$ | |
| $y=\dfrac{x+1}{x-1}$ | |
| $y=x^3-3x-1$ | |
| $y=x^2+x-1$ |
Một khung cửa kính hình parabol với đỉnh $M$ và cạnh đáy $AB$ như minh họa ở hình bên. Biết chi phí để lắp phần kính màu (phần tô đậm trong hình) là $200.000$ đồng/m$^2$ và phần kính trắng còn lại là $150.000$ đồng/m$^2$.
Cho $MN=AB=4$m và $MC=CD=DN$. Hỏi số tiền để lắp kính cho khung cửa như trên gần nhất với số tiền nào dưới đây?
| $1.954.000$ đồng | |
| $2.123.000$ đồng | |
| $1.946.000$ đồng | |
| $2.145.000$ đồng |
