Bảng biến thiên dưới đây mô tả sự biến thiên của hàm số nào?
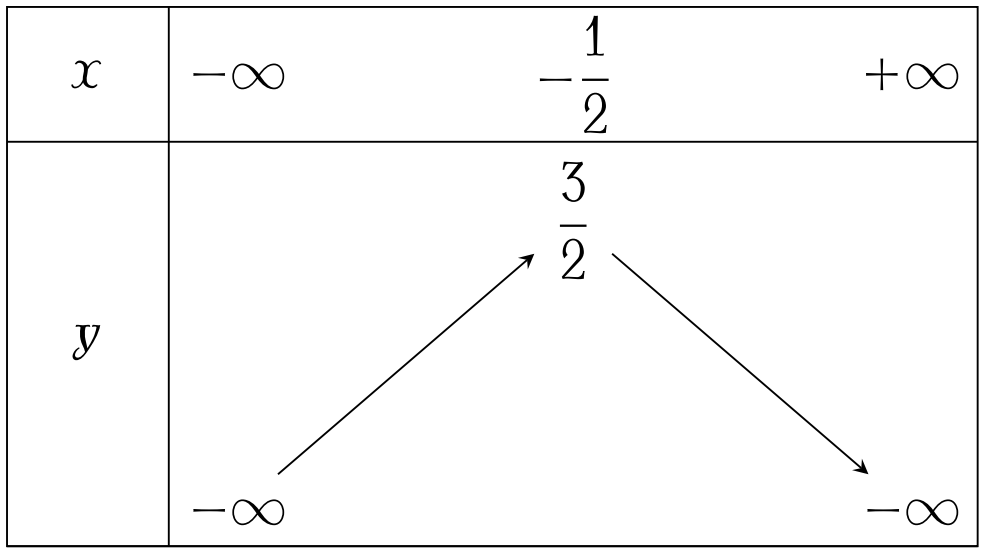
| $y=2x^2+2x-1$ | |
| $y=2x^2+2x+2$ | |
| $y=-2x^2-2$ | |
| $y=-2x^2-2x+1$ |
Bảng biến thiên dưới đây mô tả sự biến thiên của hàm số nào?
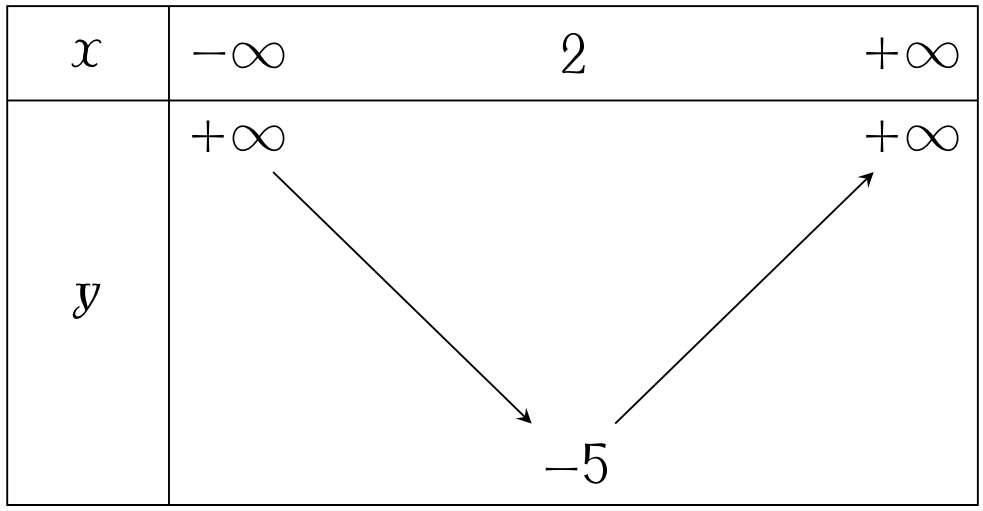
| $y=-x^2+4x-9$ | |
| $y=x^2-4x-1$ | |
| $y=-x^2+4x$ | |
| $y=x^2-4x-5$ |
Đồ thị trong hình bên là của hàm số nào sau đây?
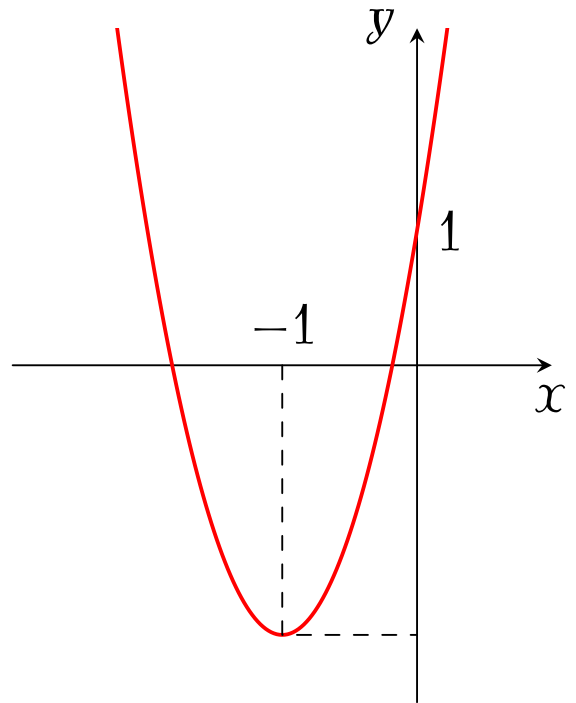
| $y=-3x^2-6x$ | |
| $y=3x^2+6x+1$ | |
| $y=x^2+2x+1$ | |
| $y=-x^2-2x+1$ |
Đồ thị trong hình bên là của hàm số nào sau đây?
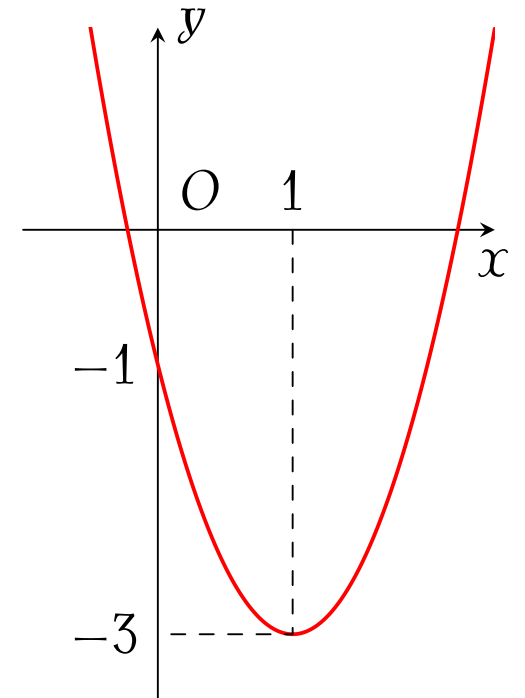
| $y=x^2-4x-1$ | |
| $y=2x^2-4x-1$ | |
| $y=-2x^2-4x-1$ | |
| $y=2x^2-4x+1$ |
Đồ thị trong hình bên là của hàm số nào sau đây?
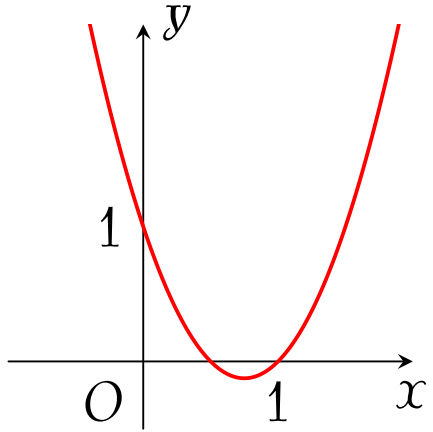
| $y=-x^2+3x-1$ | |
| $y=-2x^2+3x-1$ | |
| $y=2x^2-3x+1$ | |
| $y=x^2-3x+1$ |
Xác định parabol $\left(\mathscr{P}\right)\colon y=ax^2+bx+c$, biết rằng $\left(\mathscr{P}\right)$ đi qua ba điểm $A(1;1)$, $B(-1;-3)$ và $O(0;0)$.
| $y=x^2+2x$ | |
| $y=-x^2-2x$ | |
| $y=-x^2+2x$ | |
| $y=x^2-2x$ |
Xác định parabol $\left(\mathscr{P}\right)\colon y=2x^2+bx+c$, biết rằng $\left(\mathscr{P}\right)$ có đỉnh $I(-1;-2)$.
| $y=2x^2-4x+4$ | |
| $y=2x^2-4x$ | |
| $y=2x^2-3x+4$ | |
| $y=2x^2+4x$ |
Xác định parabol $\left(\mathscr{P}\right)\colon y=ax^2+bx+2$, biết rằng $\left(\mathscr{P}\right)$ đi qua điểm $M(1;5)$ và $N(-2;8)$.
| $y=2x^2+x+2$ | |
| $y=x^2+x+2$ | |
| $y=-2x^2+x+2$ | |
| $y=-2x^2-x+2$ |
Trong các hàm số sau, hàm số nào có đồ thị nhận đường thẳng $x=1$ làm trục đối xứng?
| $y=-2x^2+4x+1$ | |
| $y=2x^2+4x-3$ | |
| $y=2x^2-2x-1$ | |
| $y=x^2-x+2$ |
Trục đối xứng của parabol $\left(\mathscr{P}\right)\colon y=2x^2+6x+3$ là
| $x=-\dfrac{3}{2}$ | |
| $y=-\dfrac{3}{2}$ | |
| $x=-3$ | |
| $y=-3$ |
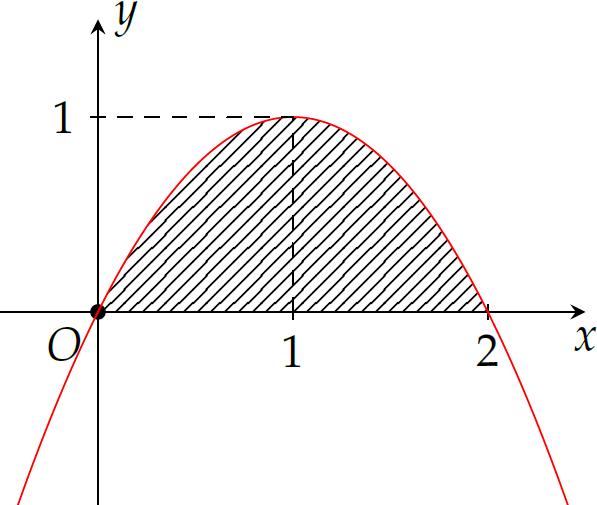
Cho hàm bậc hai \(y=f(x)\) có đồ thị như hình bên. Tính thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi đồ thị hàm số \(y=f(x)\) và \(Ox\) quanh \(Ox\).
| \(\dfrac{4\pi}{3}\) | |
| \(-\dfrac{12\pi}{15}\) | |
| \(\dfrac{16\pi}{15}\) | |
| \(\dfrac{16\pi}{5}\) |
Hàm số nào dưới đây có bảng biến thiên như sau?
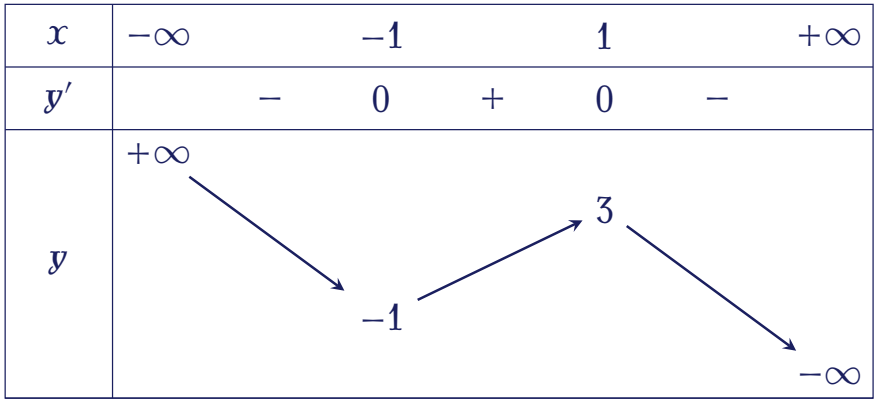
| $y=\dfrac{x+2}{x}$ | |
| $y=-x^3+3x+1$ | |
| $y=x^4-3x^2$ | |
| $y=-2x^2+1$ |
Trong các hàm số sau, hàm số nào không có cực trị?
| $y=x^2$ | |
| $y=\dfrac{x+2}{2x-1}$ | |
| $y=x^4+2x^2+2$ | |
| $y=-x^3-x^2$ |
Hàm số nào dưới đây có bảng biến thiên như hình vẽ?
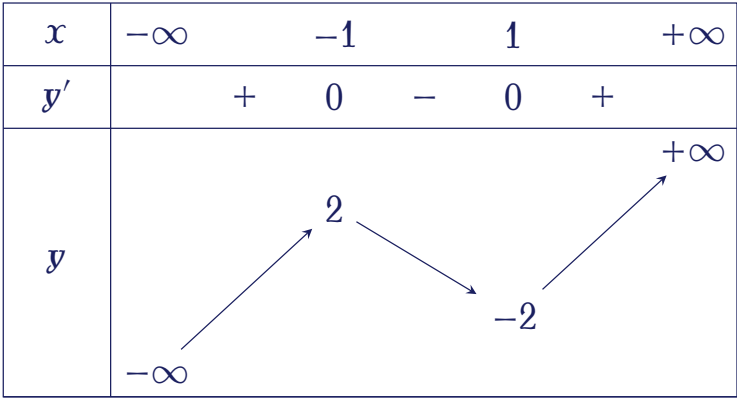
| $y=x^4-2x^2$ | |
| $y=-x^3+3x$ | |
| $y=-x^4+2x^2$ | |
| $y=x^3-3x$ |
Cho hàm số $y=x^2+4$. Khẳng định nào dưới đây đúng?
| $\displaystyle\displaystyle\int f(x)\mathrm{\,d}x=2x+C$ | |
| $\displaystyle\displaystyle\int f(x)\mathrm{\,d}x=x^2+4x+C$ | |
| $\displaystyle\displaystyle\int f(x)\mathrm{\,d}x=\dfrac{x^3}{3}+4x+C$ | |
| $\displaystyle\displaystyle\int f(x)\mathrm{\,d}x=x^3+4x+C$ |
Tính thể tích $V$ của khối tròn xoay khi cho diện tích hình phẳng giới hạn bởi đồ thị hàm số $y=2x-x^2$, trục $Ox$ quay quanh $Ox$.
| $V=\dfrac{8\pi}{15}$ | |
| $V=\dfrac{32\pi}{15}$ | |
| $V=\dfrac{4\pi}{3}$ | |
| $V=\dfrac{16\pi}{15}$ |
Tính diện tích $S$ của hình phẳng giới hạn bởi đồ thị hàm số $y=x^2-4x$, $Ox$ và $x=0,\,x=2$.
| $S=9$ | |
| $S=\dfrac{16}{3}$ | |
| $S=\dfrac{32}{3}$ | |
| $S=\dfrac{5}{3}$ |
Điện lượng truyền trong dây dẫn có phương trình $Q=t^2$. Tính cường độ dòng điện tức thời tại thời điểm $t_0=5$ (giây).
| $3$(A) | |
| $25$(A) | |
| $10$(A) | |
| $2$(A) |
Phương trình tiếp tuyến của đồ thị hàm số $y=\dfrac{1}{2}x^2-2x+1$ biết tiếp tuyến song song với đường thẳng $y=2x+3$ là
| $y=2x+5$ | |
| $y=3x+5$ | |
| $y=-2x+7$ | |
| $y=2x–7$ |
Tìm phương trình tiếp tuyến của đồ thị hàm số $y=f(x)=-3x^2+x+3$ $(\mathscr{P})$ tại điểm $M(1;1)$.
| $y=-5x+6$ | |
| $y=5x-6$ | |
| $y=-5x-6$ | |
| $y=5x+6$ |
