Bảng biến thiên dưới đây mô tả sự biến thiên của hàm số nào?
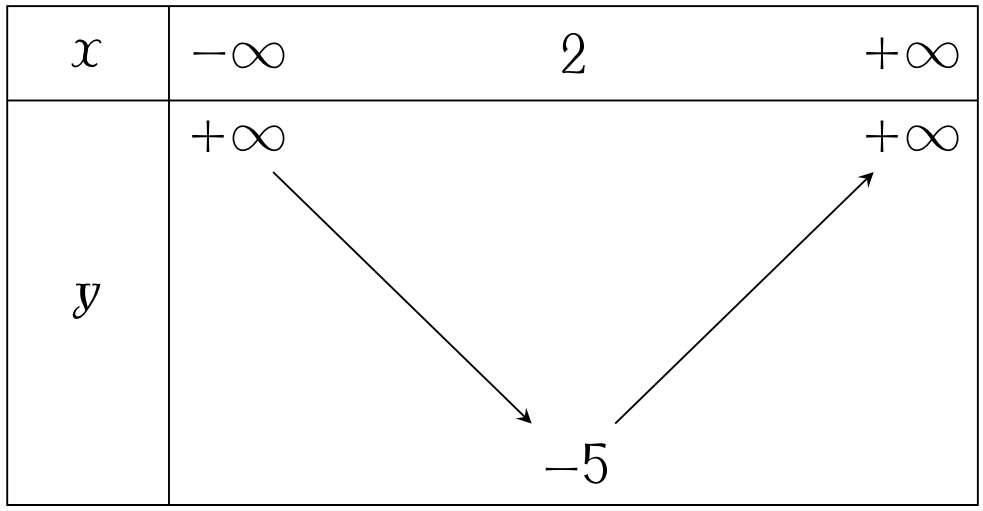
| $y=-x^2+4x-9$ | |
| $y=x^2-4x-1$ | |
| $y=-x^2+4x$ | |
| $y=x^2-4x-5$ |
Hàm số nào dưới đây có bảng biến thiên như sau?
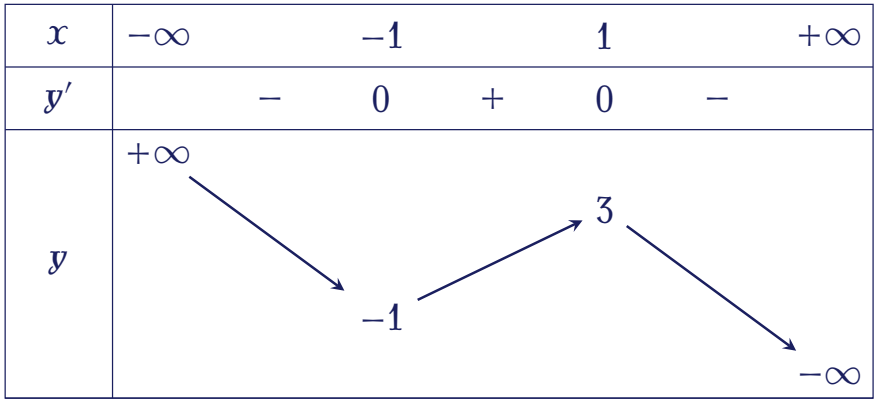
| $y=\dfrac{x+2}{x}$ | |
| $y=-x^3+3x+1$ | |
| $y=x^4-3x^2$ | |
| $y=-2x^2+1$ |
Hàm số nào dưới đây có bảng biến thiên như hình vẽ?
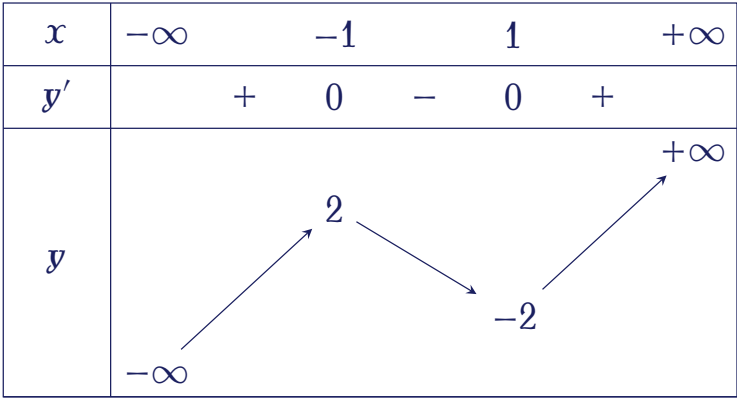
| $y=x^4-2x^2$ | |
| $y=-x^3+3x$ | |
| $y=-x^4+2x^2$ | |
| $y=x^3-3x$ |
Đồ thị trong hình bên là của hàm số nào sau đây?
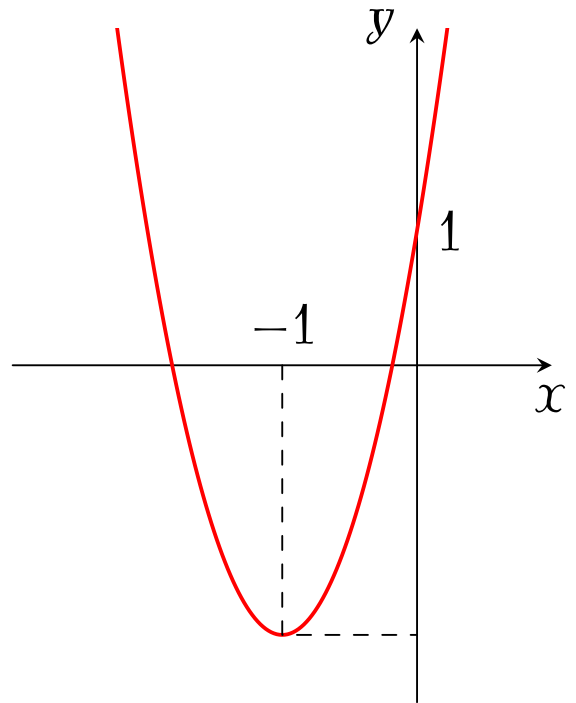
| $y=-3x^2-6x$ | |
| $y=3x^2+6x+1$ | |
| $y=x^2+2x+1$ | |
| $y=-x^2-2x+1$ |
Đồ thị trong hình bên là của hàm số nào sau đây?
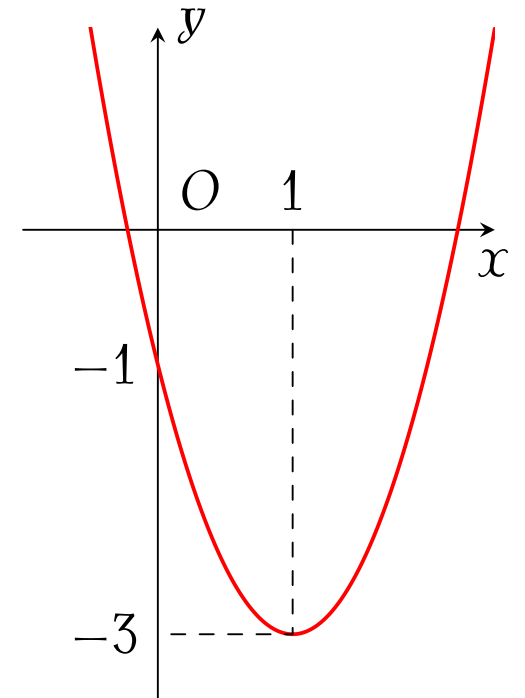
| $y=x^2-4x-1$ | |
| $y=2x^2-4x-1$ | |
| $y=-2x^2-4x-1$ | |
| $y=2x^2-4x+1$ |
Đồ thị trong hình bên là của hàm số nào sau đây?
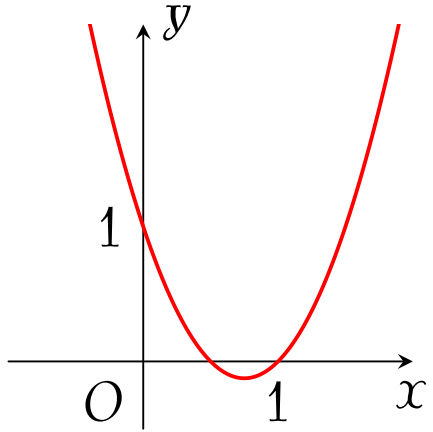
| $y=-x^2+3x-1$ | |
| $y=-2x^2+3x-1$ | |
| $y=2x^2-3x+1$ | |
| $y=x^2-3x+1$ |
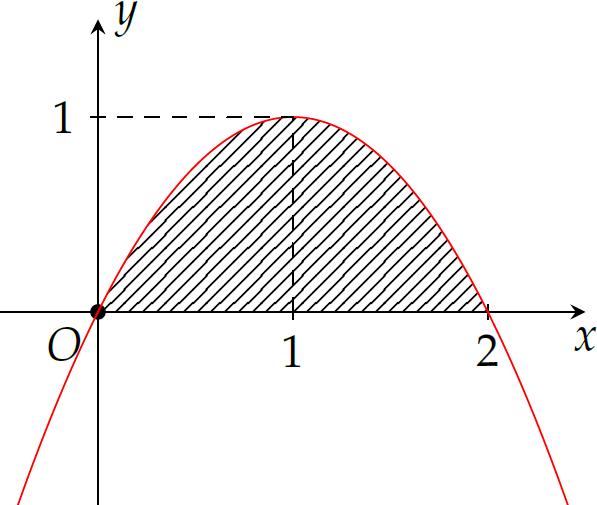
Cho hàm bậc hai \(y=f(x)\) có đồ thị như hình bên. Tính thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi đồ thị hàm số \(y=f(x)\) và \(Ox\) quanh \(Ox\).
| \(\dfrac{4\pi}{3}\) | |
| \(-\dfrac{12\pi}{15}\) | |
| \(\dfrac{16\pi}{15}\) | |
| \(\dfrac{16\pi}{5}\) |
Cho hàm số $y=f(x)$ liên tục và có bảng biến thiên trên đoạn $[-1;3]$ như hình vẽ.
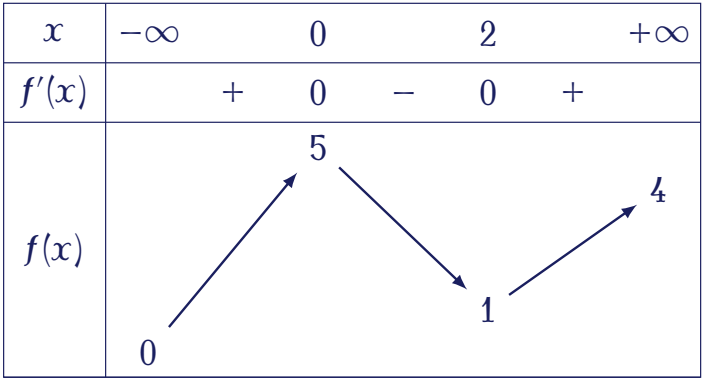
Khẳng định nào sau đây đúng?
| $\max\limits_{[-1;3]}f(x)=f(0)$ | |
| $\max\limits_{[-1;3]}f(x)=f(3)$ | |
| $\max\limits_{[-1;3]}f(x)=f(-1)$ | |
| $\max\limits_{[-1;3]}f(x)=f(2)$ |
Cho hàm số $y=f(x)$ có bảng biến thiên như sau:
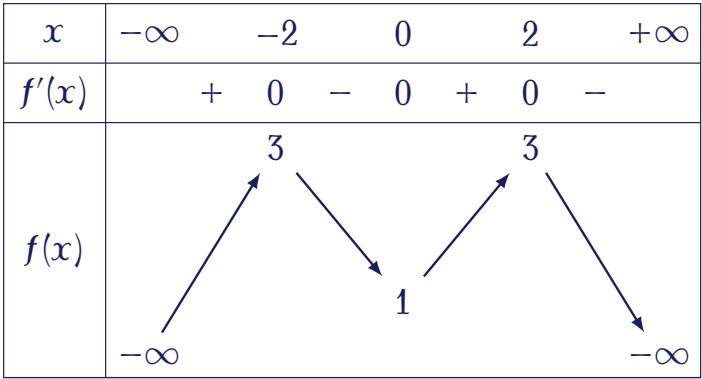
Số điểm cực tiểu của hàm số đã cho là
| $0$ | |
| $3$ | |
| $2$ | |
| $1$ |
Cho hàm số $y=f(x)$ có bảng biến thiên như hình vẽ dưới đây:
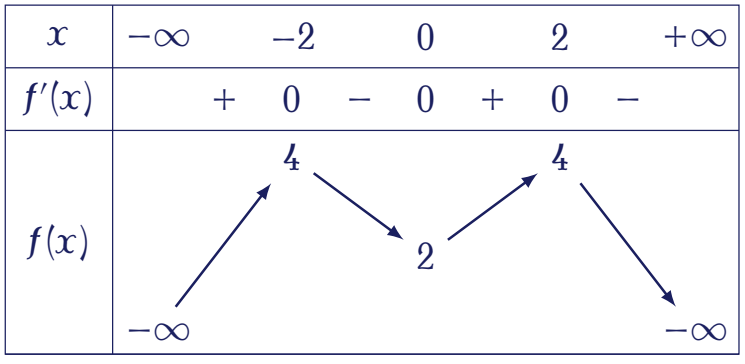
Số nghiệm của phương trình $f^2(x)-4f(x)+3=0$ là
| $5$ | |
| $3$ | |
| $6$ | |
| $4$ |
Cho hàm số $f(x)$ có bảng biến thiên như sau:
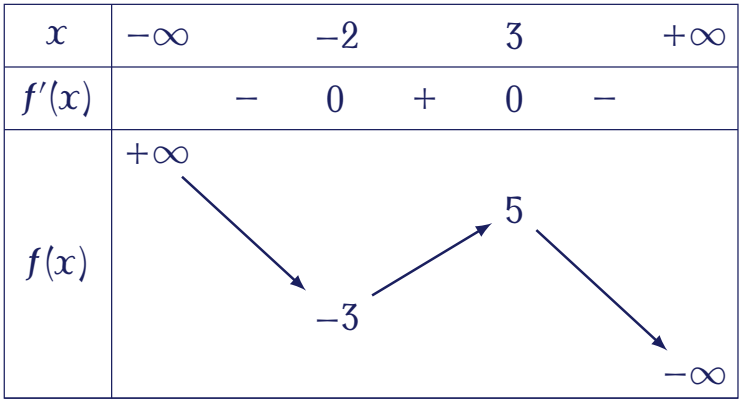
Hàm số đã cho đạt cực đại tại
| $x=-2$ | |
| $x=3$ | |
| $x=5$ | |
| $x=-3$ |
Cho hàm số $y=ax^3-3x^2+b$ ($a\neq0$) có bảng biến thiên như sau:
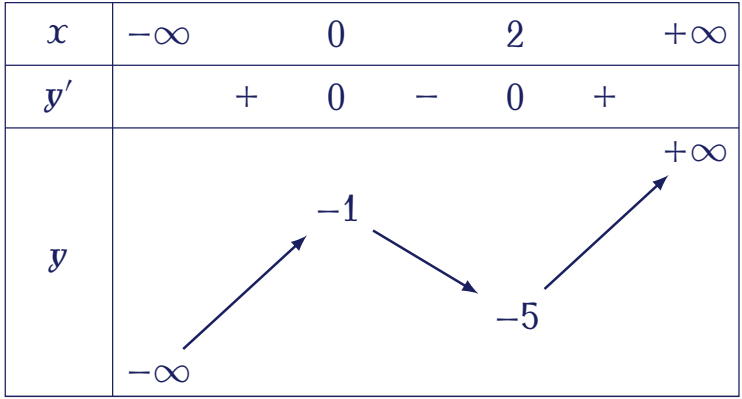
Mệnh đề nào dưới đây đúng?
| $a>0,\,b< 0$ | |
| $a< 0,\,b>0$ | |
| $a>0,\,b>0$ | |
| $a< 0,\,b< 0$ |
Cho hàm số $y=f(x)$ có bảng biến thiên trên đoạn $[-1;3]$ như sau:
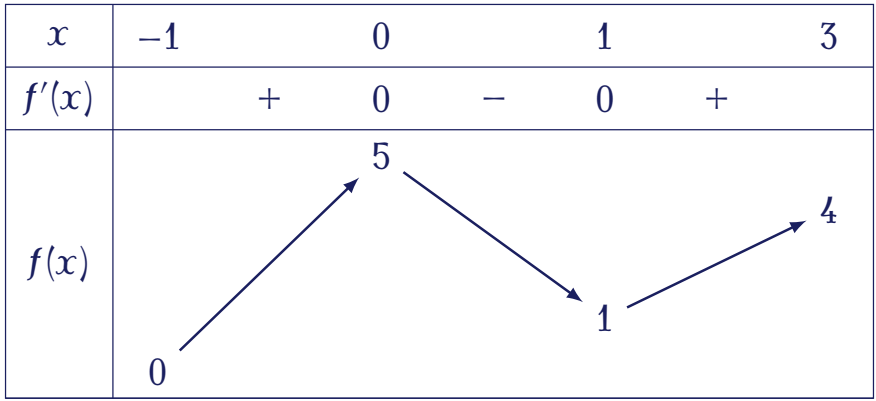
Giá trị lớn nhất của hàm số đã cho trên đoạn $[-1;3]$ bằng
| $1$ | |
| $4$ | |
| $0$ | |
| $5$ |
Cho hàm số $y=f(x)$ có bảng biến thiên như sau:
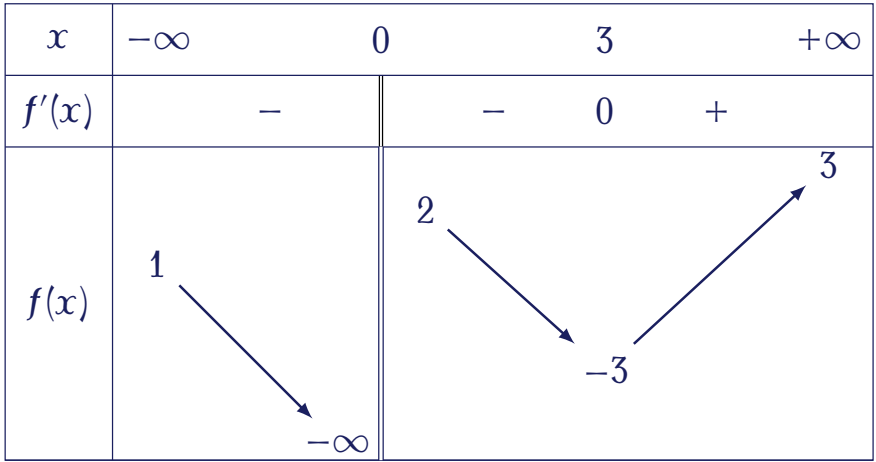
Tiệm cận đứng của đồ thị hàm số đã cho là
| $x=3$ | |
| $x=2$ | |
| $x=0$ | |
| $x=1$ |
Cho hàm số $y=f(x)$ có bảng biến thiên như sau:
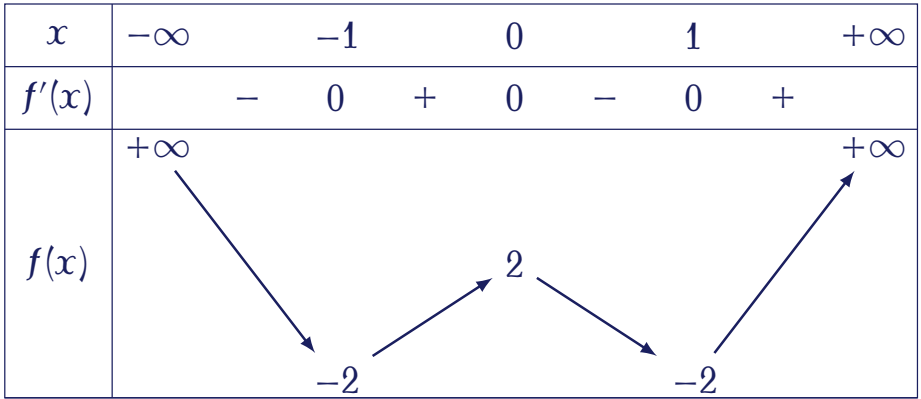
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
| $(-\infty;1)$ | |
| $(0;1)$ | |
| $(-1;0)$ | |
| $(-2;+\infty)$ |
Cho hàm số $y=f(x)$ có bảng biến thiên như sau:
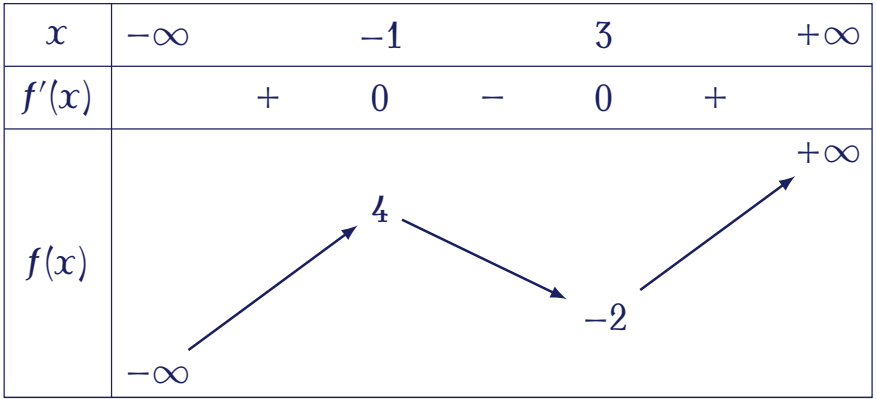
Giá trị cực đại của hàm số đã cho bằng
| $-2$ | |
| $-1$ | |
| $4$ | |
| $3$ |
Cho hàm số $y=f(x)$ có bảng biến thiên như hình vẽ sau:
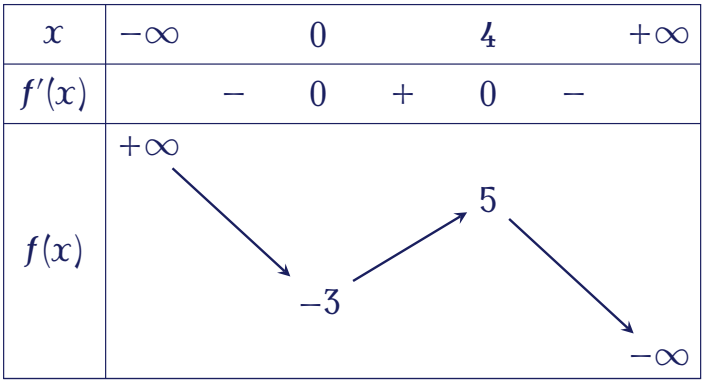
Giá trị lớn nhất của hàm số $g(x)=f\big(4x-x^2\big)+\dfrac{x^3}{3}-3x^2+8x+\dfrac{1}{3}$ trên đoạn $[1;3]$ bằng
| $15$ | |
| $\dfrac{25}{3}$ | |
| $\dfrac{19}{3}$ | |
| $12$ |
Cho hàm số $y=f(x)$ có bảng biến thiên như sau:
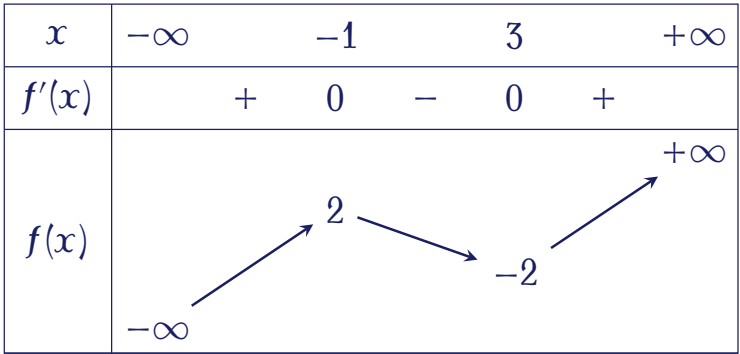
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
| $(-\infty;2)$ | |
| $(1;+\infty)$ | |
| $(1;3)$ | |
| $(-\infty;1)$ |
Cho hàm số $y=f(x)$ có bảng biến thiên như sau:
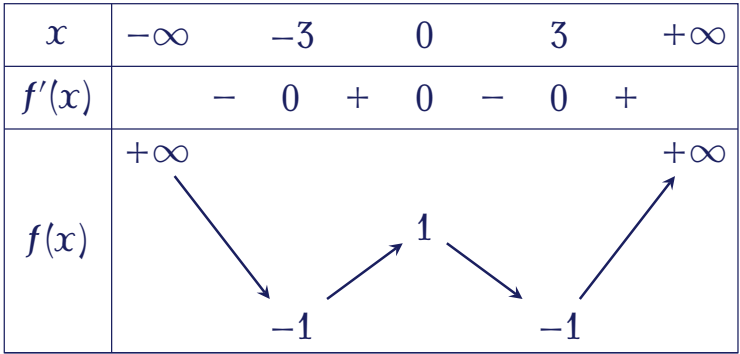
Số điểm cực trị của hàm số đã cho bằng
| $1$ | |
| $2$ | |
| $3$ | |
| $0$ |
Cho hàm số $y=f(x)$ có bảng biến thiên như sau:
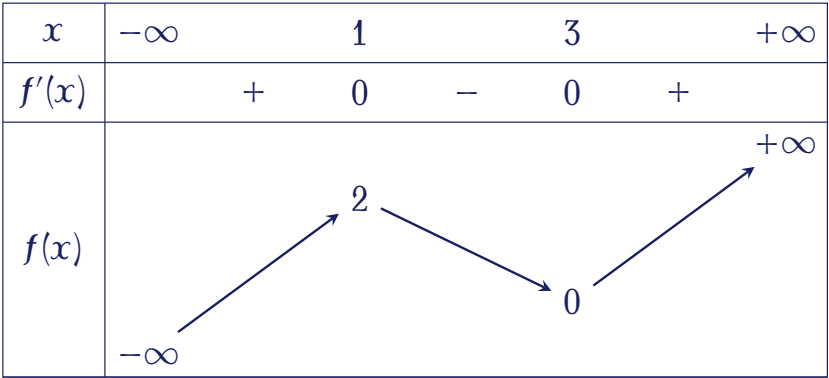
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
| $(0;2)$ | |
| $(3;+\infty)$ | |
| $(-\infty;1)$ | |
| $(1;3)$ |
