Trong mặt phẳng $Oxy$, cho tam giác $ABC$ có $M\left(-\dfrac{5}{2};-1\right)$, $N\left(-\dfrac{3}{2};-\dfrac{7}{2}\right)$, $P\left(0;\dfrac{1}{2}\right)$ lần lượt là trung điểm các cạnh $BC$, $CA$ và $AB$. Tìm tọa độ trọng tâm $G$ của tam giác $ABC$.
| $G\left(-\dfrac{4}{3};-\dfrac{4}{3}\right)$ | |
| $G(-4;-4)$ | |
| $G\left(\dfrac{4}{3};-\dfrac{4}{3}\right)$ | |
| $G(4;-4)$ |
Cho tam giác $ABC$. Biết trung điểm của các cạnh $BC$, $CA$, $AB$ có tọa độ lần lượt là $M(1;-1)$, $N(3;2)$, $P(0;-5)$. Khi đó tọa độ của điểm $A$ là
| $(-2;2)$ | |
| $(5;1)$ | |
| $\left(\sqrt{5};0\right)$ | |
| $\left(2;\sqrt{2}\right)$ |
Cho tam giác \(ABC\). Gọi \(M,\,N\) lần lượt là trung điểm của \(AB\) và \(AC\). Khẳng định nào sau đây sai?
| \(\overrightarrow{AB}=2\overrightarrow{AM}\) | |
| \(\overrightarrow{AC}=2\overrightarrow{NC}\) | |
| \(\overrightarrow{CB}=-2\overrightarrow{MN}\) | |
| \(\overrightarrow{CN}=-\dfrac{1}{2}\overrightarrow{AC}\) |
Gọi $z_1,\,z_2$ là hai nghiệm phức của phương trình $z^2-6z+14=0$ và $M,\,N$ lần lượt là điểm biểu diễn của $z_1,\,z_2$ trên mặt phẳng tọa độ. Trung điểm của đoạn $MN$ có tọa độ là
| $(3;7)$ | |
| $(-3;0)$ | |
| $(3;0)$ | |
| $(-3;7)$ |
Gọi $A,\,B,\,C$ là điểm biểu diễn cho các số phức $z_1=-2+3i$, $z_2=-4-2i$, $z_3=3+i$. Khi đó tọa độ trọng tâm $G$ của tam giác $ABC$ là
| $\left(-1;-\dfrac{2}{3}\right)$ | |
| $\left(-1;\dfrac{2}{3}\right)$ | |
| $\left(1;-\dfrac{2}{3}\right)$ | |
| $\left(1;\dfrac{2}{3}\right)$ |
Trong mặt phẳng $Oxy$, cho tam giác $PQR$ có $P(-3;2)$, $Q(1;1)$, $R(2;-4)$. Gọi $P',\,Q',\,R'$ lần lượt là ảnh của $P,\,Q,\,R$ qua phép vị tự tâm $O$ tỉ số $k=-\dfrac{1}{3}$. Khi đó tọa độ trọng tâm của tam giác $P'Q'R'$ là
| $\left(\dfrac{1}{9};\dfrac{1}{3}\right)$ | |
| $\left(0;\dfrac{1}{9}\right)$ | |
| $\left(\dfrac{2}{3};-\dfrac{1}{3}\right)$ | |
| $\left(\dfrac{2}{9};0\right)$ |
Trong mặt phẳng $Oxy$, cho hai đường thẳng song song $d\colon2x-3y-1=0$ và $d'\colon2x-3y+5=0$. Phép tịnh tiến theo vectơ nào sau đây không thể biến $d$ thành $d'$?
| $\overrightarrow{u}=(0;2)$ | |
| $\overrightarrow{u}=(-3;0)$ | |
| $\overrightarrow{u}=(3;4)$ | |
| $\overrightarrow{u}=(-1;1)$ |
Trong mặt phẳng $Oxy$, cho đường thẳng $d\colon2x-y+1=0$. Để phép tịnh tiến theo vectơ $\overrightarrow{v}$ biến $d$ thành chính nó thì $\overrightarrow{v}$ có thể là vectơ nào sau đây?
| $\overrightarrow{v}=(2;1)$ | |
| $\overrightarrow{v}=(2;-1)$ | |
| $\overrightarrow{v}=(1;2)$ | |
| $\overrightarrow{v}=(-1;2)$ |
Trong mặt phẳng $Oxy$, cho hai đường thẳng song song $d\colon x+y+1=0$ và $d'\colon x+y-1=0$. Biết rằng phép tịnh tiến $\mathrm{T}_{\overrightarrow{v}}$ biến đường thẳng $d$ thành đường thẳng $d'$ và vectơ $\overrightarrow{v}$ cùng phương với vectơ đơn vị $\overrightarrow{i}$. Hãy tìm tọa độ vectơ $\overrightarrow{v}$.
| $\overrightarrow{v}=(2;0)$ | |
| $\overrightarrow{v}=(0;2)$ | |
| $\overrightarrow{v}=(0;-2)$ | |
| $\overrightarrow{v}=(-2;0)$ |
Cho lưới tọa độ như hình vẽ.
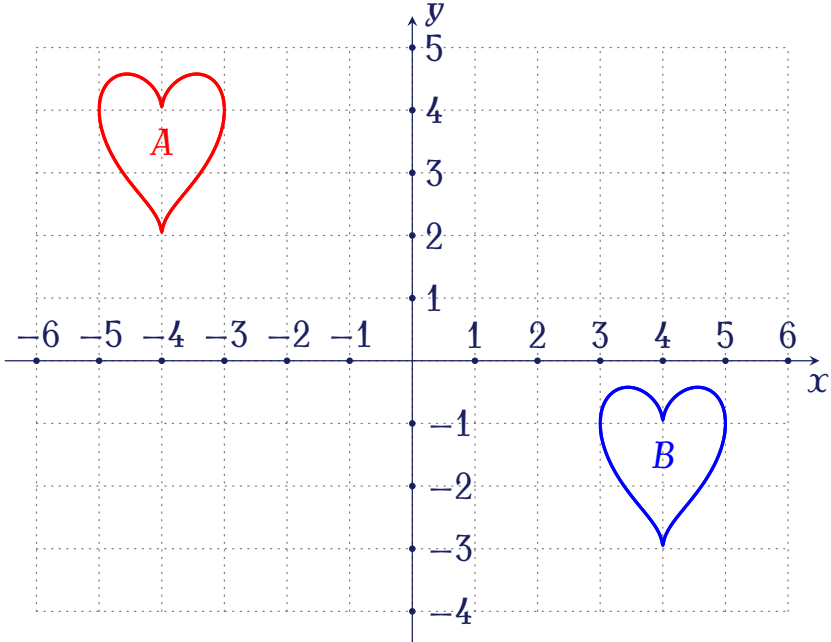
Tìm tọa độ vectơ $\overrightarrow{v}$ biết rằng phép tịnh tiến $\mathrm{T}_{\overrightarrow{v}}$ biến hình $A$ thành hình $B$.
| $\overrightarrow{v}=(8;-5)$ | |
| $\overrightarrow{v}=(-8;5)$ | |
| $\overrightarrow{v}=(8;-3)$ | |
| $\overrightarrow{v}=(8;3)$ |
Cho lưới tọa độ như hình vẽ.
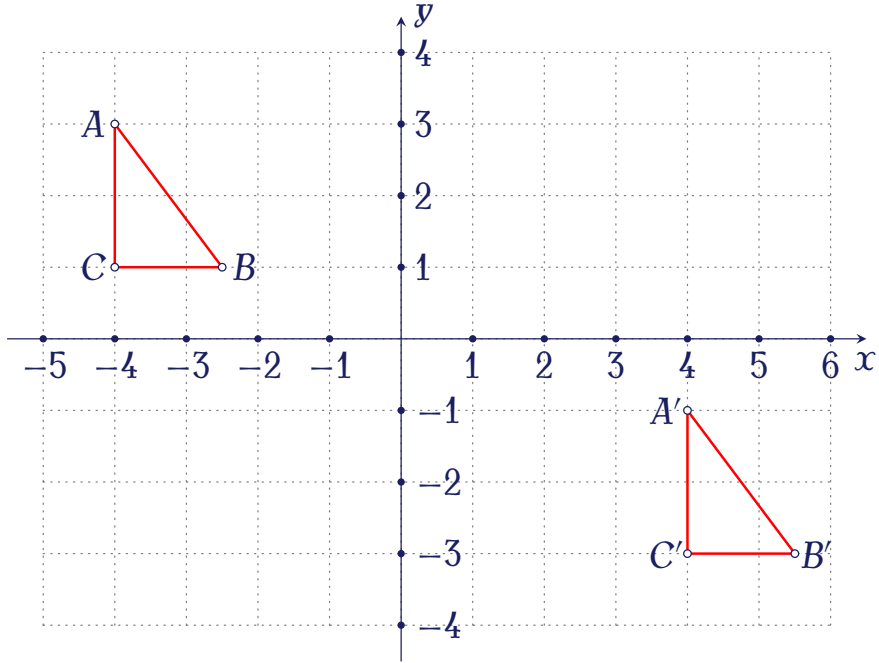
Tìm tọa độ vectơ $\overrightarrow{v}$ biết rằng phép tịnh tiến $\mathrm{T}_{\overrightarrow{v}}$ biến tam giác $ABC$ thành tam giác $A'B'C'$.
| $\overrightarrow{v}=(8;-4)$ | |
| $\overrightarrow{v}=(-8;4)$ | |
| $\overrightarrow{v}=(8;-3)$ | |
| $\overrightarrow{v}=(8;3)$ |
Biết rằng phép tịnh tiến theo vectơ $\overrightarrow{v}$ biến điểm $A(1;3)$ thành điểm $A'(1;7)$. Tìm tọa độ vectơ $\overrightarrow{v}$.
| $(0;-4)$ | |
| $(4;0)$ | |
| $(0;4)$ | |
| $(0;5)$ |
Trong mặt phẳng $Oxy$, gọi $N(2;1)$ là ảnh của điểm $M(1;-2)$ qua phép tịnh tiến $\mathrm{T}_{\overrightarrow{u}}$. Tọa độ vectơ $\overrightarrow{u}$ là
| $(1;-3)$ | |
| $(-1;3)$ | |
| $(3;-1)$ | |
| $(1;3)$ |
Gọi $M, N$ lần lượt là điểm biểu diễn hình học các số phức $z=4+i$ và $w=2+3 i$. Tọa độ trung điểm $I$ của đoạn thẳng $MN$ là
| $(2;-2)$ | |
| $(-2;2)$ | |
| $(3;2)$ | |
| $\left(\dfrac{3}{2};\dfrac{7}{2}\right)$ |
Trong mặt phẳng $Oxy$, cho các điểm $A(1;3)$, $B(4;0)$, $C(2;-5)$. Tọa độ điểm $M$ thỏa mãn $\overrightarrow{MA}+\overrightarrow{MB}-3\overrightarrow{MC}=\overrightarrow{0}$ là
| $M\left(1;18\right)$ | |
| $M\left(-1;18\right)$ | |
| $M\left(1;-18\right)$ | |
| $M\left(-18;1\right)$ |
Trong mặt phẳng $Oxy$, cho tam giác $MNP$ có $M(-2;1)$, $N(1;3)$, $P(0;2)$. Tọa độ trọng tâm $G$ của tam giác $MNP$ là
| $(2;1)$ | |
| $\left(2;\dfrac{-1}{3}\right)$ | |
| $\left(-\dfrac{1}{3};2\right)$ | |
| $(1;2)$ |
Trong mặt phẳng $Oxy$, cho $2$ điểm $A\left(2;-5\right)$, $B\left(-1;3\right)$. Tọa độ vectơ $\overrightarrow{AB}$ là
| $\overrightarrow{AB}=\left(1;-2\right)$ | |
| $\overrightarrow{AB}=\left(-3;8\right)$ | |
| $\overrightarrow{AB}=\left(3;-8\right)$ | |
| $\overrightarrow{AB}=\left(-2;-15\right)$ |
Trong mặt phẳng $Oxy$, cho hai điểm $A\left(1;0\right)$ và $B\left(0;-2\right)$. Tọa độ trung điểm của đoạn thẳng $AB$ là
| $\left(\dfrac{1}{2};-1\right)$ | |
| $\left(-1;\dfrac{1}{2}\right)$ | |
| $\left(\dfrac{1}{2};-2\right)$ | |
| $\left(1;-1\right)$ |
Trong mặt phẳng $Oxy$, cho tam giác $ABC$ có trọng tâm là gốc tọa độ $O$ hai đỉnh $A\left(-2;2\right)$ và $B\left(3;5\right)$. Tọa độ đỉnh $C$ là
| $\left(-1;-7\right)$ | |
| $\left(2;-2\right)$ | |
| $\left(-3;-5\right)$ | |
| $\left(1;7\right)$ |
Trong mặt phẳng $Oxy$, cho các vectơ $\overrightarrow{a}=(0;1)$, $\overrightarrow{b}=(-1;2)$, $\overrightarrow{c}=(-3;-2)$. Tọa độ của vectơ $\overrightarrow{u}=3\overrightarrow{a}+2\overrightarrow{b}-4\overrightarrow{c}$ là
| $(10;-15)$ | |
| $(15;10)$ | |
| $(10;15)$ | |
| $(-10;15)$ |
