Gọi $z_1,\,z_2$ là hai nghiệm phức của phương trình $z^2-6z+14=0$ và $M,\,N$ lần lượt là điểm biểu diễn của $z_1,\,z_2$ trên mặt phẳng tọa độ. Trung điểm của đoạn $MN$ có tọa độ là

	$(3;7)$
	$(-3;0)$
	$(3;0)$
	$(-3;7)$

Gọi $M, N$ lần lượt là điểm biểu diễn hình học các số phức $z=4+i$ và $w=2+3 i$. Tọa độ trung điểm $I$ của đoạn thẳng $MN$ là

	$(2;-2)$
	$(-2;2)$
	$(3;2)$
	$\left(\dfrac{3}{2};\dfrac{7}{2}\right)$

Trong mặt phẳng $Oxy$, cho hai điểm $A\left(1;0\right)$ và $B\left(0;-2\right)$. Tọa độ trung điểm của đoạn thẳng $AB$ là

	$\left(\dfrac{1}{2};-1\right)$
	$\left(-1;\dfrac{1}{2}\right)$
	$\left(\dfrac{1}{2};-2\right)$
	$\left(1;-1\right)$

Trong mặt phẳng $Oxy$, cho tam giác $ABC$ có $M\left(-\dfrac{5}{2};-1\right)$, $N\left(-\dfrac{3}{2};-\dfrac{7}{2}\right)$, $P\left(0;\dfrac{1}{2}\right)$ lần lượt là trung điểm các cạnh $BC$, $CA$ và $AB$. Tìm tọa độ trọng tâm $G$ của tam giác $ABC$.

	$G\left(-\dfrac{4}{3};-\dfrac{4}{3}\right)$
	$G(-4;-4)$
	$G\left(\dfrac{4}{3};-\dfrac{4}{3}\right)$
	$G(4;-4)$

Trong mặt phẳng $Oxy$, cho $A(4;1)$, $B(3;2)$. Tìm tọa độ $M$ sao cho $B$ là trung điểm đoạn thẳng $AM$.

	$\left(2;1\right)$
	$\left(3;2\right)$
	$\left(2;3\right)$
	$\left(5;0\right)$

Trong mặt phẳng $Oxy$, cho hai điểm $A(3;-5)$, $B(1;7)$. Trung điểm $I$ của đoạn thẳng $AB$ có tọa độ là

	$I(2;-1)$
	$I(-2;12)$
	$I(4;2)$
	$I(2;1)$

Cho tam giác $ABC$. Biết trung điểm của các cạnh $BC$, $CA$, $AB$ có tọa độ lần lượt là $M(1;-1)$, $N(3;2)$, $P(0;-5)$. Khi đó tọa độ của điểm $A$ là

	$(-2;2)$
	$(5;1)$
	$\left(\sqrt{5};0\right)$
	$\left(2;\sqrt{2}\right)$

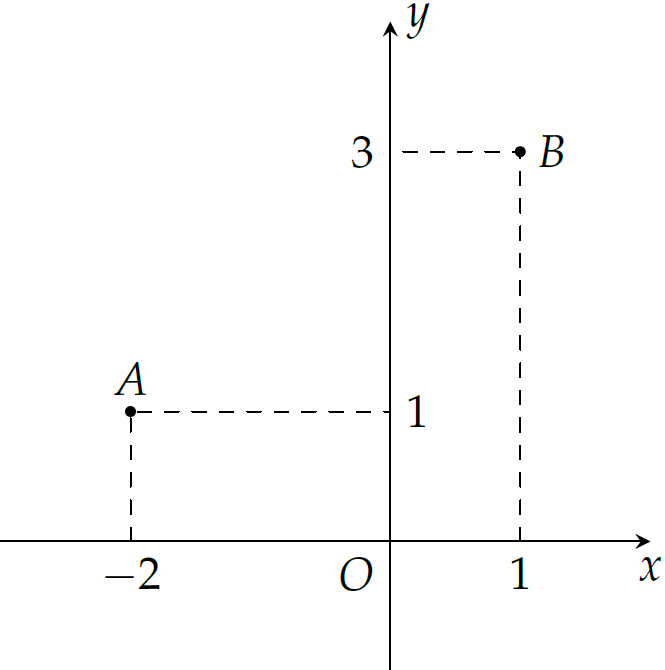
Trong mặt phẳng \(Oxy\), cho các điểm \(A,\,B\) như hình vẽ trên. Trung điểm của đoạn thẳng \(AB\) biểu diễn số phức

	\(-\dfrac{1}{2}+2i\)
	\(2-\dfrac{1}{2}i\)
	\(-1+2i\)
	\(2-i\)

Gọi \(A,\,B\) lần lượt biểu diễn các số phức \(z_1=-2+3\mathrm{i}\) và \(z_2=4-3\mathrm{i}\). Khẳng định nào sau đây đúng?

	\(A,\,B\) đối xứng nhau qua gốc tọa độ
	\(A,\,B\) đối xứng nhau qua trục hoành
	\(A,\,B\) đối xứng nhau qua trục tung
	\(A,\,B\) đối xứng nhau qua điểm \(I(1;0)\)

Trong mặt phẳng \(Oxy\), cho hai điểm \(A(2;-3)\), \(B(4;7)\). Tìm tọa độ trung điểm \(I\) của đoạn thẳng \(AB\).

	\(I(6;4)\)
	\(I(2;0)\)
	\(I(3;2)\)
	\(I(8;-21)\)

Gọi $A,\,B,\,C$ là điểm biểu diễn cho các số phức $z_1=-2+3i$, $z_2=-4-2i$, $z_3=3+i$. Khi đó tọa độ trọng tâm $G$ của tam giác $ABC$ là

	$\left(-1;-\dfrac{2}{3}\right)$
	$\left(-1;\dfrac{2}{3}\right)$
	$\left(1;-\dfrac{2}{3}\right)$
	$\left(1;\dfrac{2}{3}\right)$

Cho $z_1=5+3i$, $z_2=-8+9i$. Tọa độ điểm biểu diễn hình học của $z=z_1+z_2$ là

	$P(3;-12)$
	$Q(3;12)$
	$M(14;-5)$
	$N(-3;12)$

Trên mặt phẳng tọa độ, điểm biểu diễn số phức $z=2-7i$ có tọa độ là

	$(2;7)$
	$(-2;7)$
	$(2;-7)$
	$(-7;2)$

Trong mặt phẳng $Oxy$, phép quay tâm $O$ góc quay $-90^\circ$ biến $M(-3;5)$ thành điểm có tọa độ

	$(-5;-3)$
	$(5;-3)$
	$(5;3)$
	$(-5;3)$

Trong mặt phẳng $Oxy$, cho điểm $A(1;0)$. Ảnh của $A$ qua phép quay tâm $O$ góc quay $90^\circ$ là

	$A’(0;-1)$
	$A’(-1;0)$
	$A’(0;1)$
	$A’(1;1)$

Trong mặt phẳng $Oxy$, cho điểm $M(1;-3)$. Ảnh của điểm M qua phép tịnh tiến theo vectơ $\overrightarrow{v}=(1;-2)$ là

	$M’(2;5)$
	$M’(2;-5)$
	$M’(0;-1)$
	$M’(0;-5)$

Trong mặt phẳng $Oxy$, cho tam giác $PQR$ có $P(-3;2)$, $Q(1;1)$, $R(2;-4)$. Gọi $P',\,Q',\,R'$ lần lượt là ảnh của $P,\,Q,\,R$ qua phép vị tự tâm $O$ tỉ số $k=-\dfrac{1}{3}$. Khi đó tọa độ trọng tâm của tam giác $P'Q'R'$ là

	$\left(\dfrac{1}{9};\dfrac{1}{3}\right)$
	$\left(0;\dfrac{1}{9}\right)$
	$\left(\dfrac{2}{3};-\dfrac{1}{3}\right)$
	$\left(\dfrac{2}{9};0\right)$

Trong mặt phẳng $Oxy$, tìm ảnh $A'$ của điểm $A(1;2)$ qua phép vị tự tâm $I(3;-1)$ tỉ số $k=2$.

	$A'(3;4)$
	$A'(1;5)$
	$A'(-5;-1)$
	$A'(-1;5)$

Trong mặt phẳng $Oxy$, tìm ảnh $A'$ của điểm $A(1;-3)$ qua phép vị tự tâm $O$ tỉ số $-2$.

	$A'(2;6)$
	$A'(1;3)$
	$A'(-2;6)$
	$A'(-2;-6)$

Trong mặt phẳng $Oxy$, điểm $M'(3;-2)$ là ảnh của điểm nào sau đây qua phép quay $Q_{(O,180^\circ)}$?

	$M(3;2)$
	$M(2;3)$
	$M(-3;2)$
	$M(-2;-3)$