Trong mặt phẳng $Oxy$, cho ba vectơ $\overrightarrow{x}=(2;3)$, $\overrightarrow{y}=(-2;0)$, $\overrightarrow{u}=(6;6)$. Tìm $m+n$ biết $\overrightarrow{u}=m\overrightarrow{x}+n\overrightarrow{y}$.
| $3$ | |
| $1$ | |
| $2$ | |
| $4$ |
Trong mặt phẳng $Oxy$, cho các véc-tơ $\overrightarrow{u}=(2;-4)$, $\overrightarrow{a}=(-1;-2)$, $\overrightarrow{b}=(1;-3)$. Biết $\overrightarrow{u}=m\overrightarrow{a}+n\overrightarrow{b}$. Tính $m-n$ được kết quả là
| $5$ | |
| $-2$ | |
| $-5$ | |
| $2$ |
Trong mặt phẳng \(Oxy\), cho các vectơ \(\vec{a}=(2;1)\), \(\vec{b}=(3;4)\) và \(\vec{c}=(7;2)\). Tìm giá trị của \(k,\,h\) sao cho $$\vec{c}=k\vec{a}+h\vec{b}$$
| \(\begin{cases}k=\dfrac{5}{2}\\ h=-\dfrac{13}{10}\end{cases}\) | |
| \(\begin{cases}k=\dfrac{23}{5}\\ h=-\dfrac{51}{10}\end{cases}\) | |
| \(\begin{cases}k=\dfrac{22}{5}\\ h=-\dfrac{3}{5}\end{cases}\) | |
| \(\begin{cases}k=\dfrac{17}{5}\\ h=-\dfrac{1}{5}\end{cases}\) |
Trong mặt phẳng \(Oxy\), cho các vectơ \(\vec{a}=(m;2)\), \(\vec{b}=(-5;1)\) và \(\vec{c}=(m;7)\). Tìm giá trị của \(m\), biết rằng \(\vec{c}=2\vec{a}+3\vec{b}\).
| \(m=-15\) | |
| \(m=3\) | |
| \(m=15\) | |
| \(m=5\) |
Trong mặt phẳng $Oxy$, cho các vectơ $\overrightarrow{u}=(3;-2)$ và $\overrightarrow{v}=\left(m^2;4\right)$ với $m$ là số thực. Tìm $m$ để $\overrightarrow{u}$ và $\overrightarrow{v}$ cùng phương.
| $m=\sqrt{6}$ | |
| $m=-6$ | |
| Không có giá trị nào của $m$ | |
| $m=\pm\sqrt{6}$ |
Trong mặt phẳng $Oxy$, cho các véc-tơ $\overrightarrow{u}=(-2;1)$ và $\overrightarrow{v}=3\overrightarrow{i}-m\overrightarrow{j}$. Tìm $m$ để hai véc-tơ $\overrightarrow{u},\,\overrightarrow{v}$ cùng phương.
| $m=-\dfrac{2}{3}$ | |
| $m=\dfrac{2}{3}$ | |
| $m=-\dfrac{3}{2}$ | |
| $m=\dfrac{3}{2}$ |
Trong mặt phẳng \(Oxy\), cho hai vectơ \(\vec{u}=2\vec{i}-\vec{j}\) và \(\vec{v}=\vec{i}+m\vec{j}\). Tìm \(m\) để \(\vec{u},\,\vec{v}\) cùng phương.
| \(m=-1\) | |
| \(m=-\dfrac{1}{2}\) | |
| \(m=\dfrac{1}{4}\) | |
| \(m=2\) |
Trong mặt phẳng \(Oxy\), cho hai vectơ \(\vec{a}=(-5;0)\) và \(\vec{b}=(4;m)\). Tìm \(m\) để \(\vec{a},\,\vec{b}\) cùng phương.
| \(m=-5\) | |
| \(m=4\) | |
| \(m=0\) | |
| \(m=-1\) |
Trong mặt phẳng tọa độ \(Oxy\), cho ba vectơ \(\vec{a}=(4;-1)\), \(\vec{b}=(1;-1)\) và \(\vec{c}=(2;1)\). Chọn mệnh đề đúng.
| \(\vec{a}=\vec{b}-2\vec{c}\) | |
| \(\vec{a}=2\vec{b}-\vec{c}\) | |
| \(\vec{a}=2\vec{b}+\vec{c}\) | |
| \(\vec{a}=\vec{b}+\vec{c}\) |
Cho vectơ \(\vec{a}=(1;-2)\). Với giá trị nào của \(y\) thì vectơ \(\vec{b}=(-3;y)\) vuông góc với \(\vec{a}\)?
| \(-6\) | |
| \(6\) | |
| \(-\dfrac{3}{2}\) | |
| \(3\) |
Trong mặt phẳng \(Oxy\), cho ba điểm \(A(3;6)\), \(B(x;-2)\) và \(C(2;y)\). Tính \(\overrightarrow{OA}\cdot\overrightarrow{BC}\) theo \(x\) và \(y\).
| \(\overrightarrow{OA}\cdot\overrightarrow{BC}=-3x+6y+12\) | |
| \(\overrightarrow{OA}\cdot\overrightarrow{BC}=0\) | |
| \(\overrightarrow{OA}\cdot\overrightarrow{BC}=-3x+6y+18\) | |
| \(\overrightarrow{OA}\cdot\overrightarrow{BC}=3x+6y-12\) |
Trong không gian \(Oxyz\), cho điểm \(M(1;-1;2)\) và hai đường thẳng \(d_1\colon\begin{cases}x=t\\ y=1-t\\ z=-1\end{cases}\), \(d_2\colon\dfrac{x+1}{2}=\dfrac{y-1}{1}=\dfrac{z+2}{1}\). Đường thẳng \(\Delta\) đi qua \(M\) và cắt cả hai đường thẳng \(d_1\), \(d_2\) có vectơ chỉ phương là \(\vec{u}=(1;a;b)\). Tính \(a+b\).
| \(a+b=1\) | |
| \(a+b=-1\) | |
| \(a+b=-2\) | |
| \(a+b=2\) |
Trong mặt phẳng $Oxy$, cho bốn điểm $A(-1;2)$, $B(3;-1)$, $A'(9;-4)$, $B'(5;-1)$. Phép quay tâm $I(a;b)$ biến điểm $A$ thành $A'$, điểm $B$ thành $B'$, khi đó giá trị $a+b$ bằng
| $5$ | |
| $4$ | |
| $3$ | |
| $2$ |
Trong mặt phẳng $Oxy$, cho hai đường thẳng song song $d\colon2x-3y-1=0$ và $d'\colon2x-3y+5=0$. Phép tịnh tiến theo vectơ nào sau đây không thể biến $d$ thành $d'$?
| $\overrightarrow{u}=(0;2)$ | |
| $\overrightarrow{u}=(-3;0)$ | |
| $\overrightarrow{u}=(3;4)$ | |
| $\overrightarrow{u}=(-1;1)$ |
Trong mặt phẳng $Oxy$, cho đường thẳng $d\colon2x-y+1=0$. Để phép tịnh tiến theo vectơ $\overrightarrow{v}$ biến $d$ thành chính nó thì $\overrightarrow{v}$ có thể là vectơ nào sau đây?
| $\overrightarrow{v}=(2;1)$ | |
| $\overrightarrow{v}=(2;-1)$ | |
| $\overrightarrow{v}=(1;2)$ | |
| $\overrightarrow{v}=(-1;2)$ |
Trong mặt phẳng $Oxy$, cho hai đường thẳng song song $d\colon x+y+1=0$ và $d'\colon x+y-1=0$. Biết rằng phép tịnh tiến $\mathrm{T}_{\overrightarrow{v}}$ biến đường thẳng $d$ thành đường thẳng $d'$ và vectơ $\overrightarrow{v}$ cùng phương với vectơ đơn vị $\overrightarrow{i}$. Hãy tìm tọa độ vectơ $\overrightarrow{v}$.
| $\overrightarrow{v}=(2;0)$ | |
| $\overrightarrow{v}=(0;2)$ | |
| $\overrightarrow{v}=(0;-2)$ | |
| $\overrightarrow{v}=(-2;0)$ |
Trong mặt phẳng $Oxy$, cho vectơ $\overrightarrow{v}=(-3;1)$ và parabol $(\mathscr{P})\colon y=1-x^2$. Phép tịnh tiến $\mathrm{T}_{\overrightarrow{v}}$ biến $(\mathscr{P})$ thành parabol $(\mathscr{P}')\colon y=ax^2+bx+c$. Tính $M=b+c-a$.
| $M=-1$ | |
| $M=2$ | |
| $M=11$ | |
| $M=-12$ |
Cho lưới tọa độ như hình vẽ.
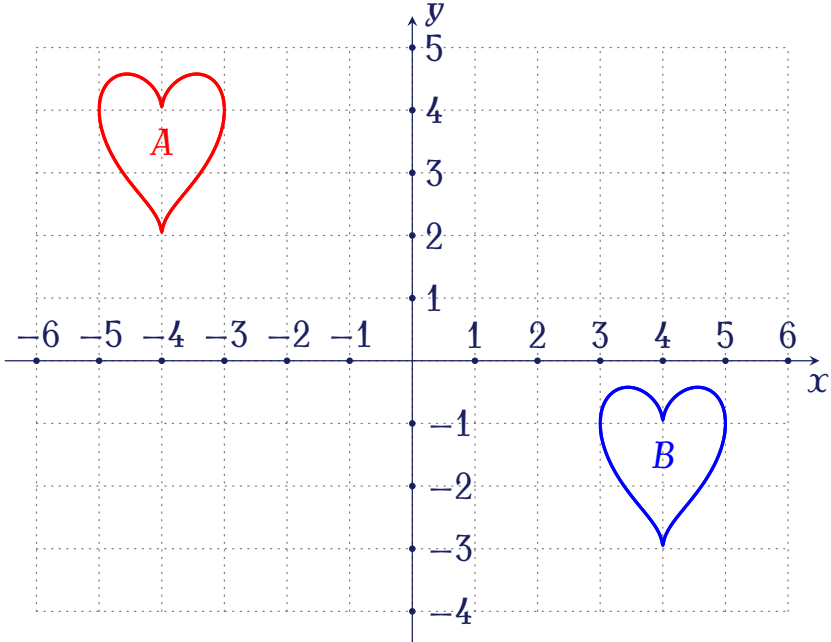
Tìm tọa độ vectơ $\overrightarrow{v}$ biết rằng phép tịnh tiến $\mathrm{T}_{\overrightarrow{v}}$ biến hình $A$ thành hình $B$.
| $\overrightarrow{v}=(8;-5)$ | |
| $\overrightarrow{v}=(-8;5)$ | |
| $\overrightarrow{v}=(8;-3)$ | |
| $\overrightarrow{v}=(8;3)$ |
Cho lưới tọa độ như hình vẽ.
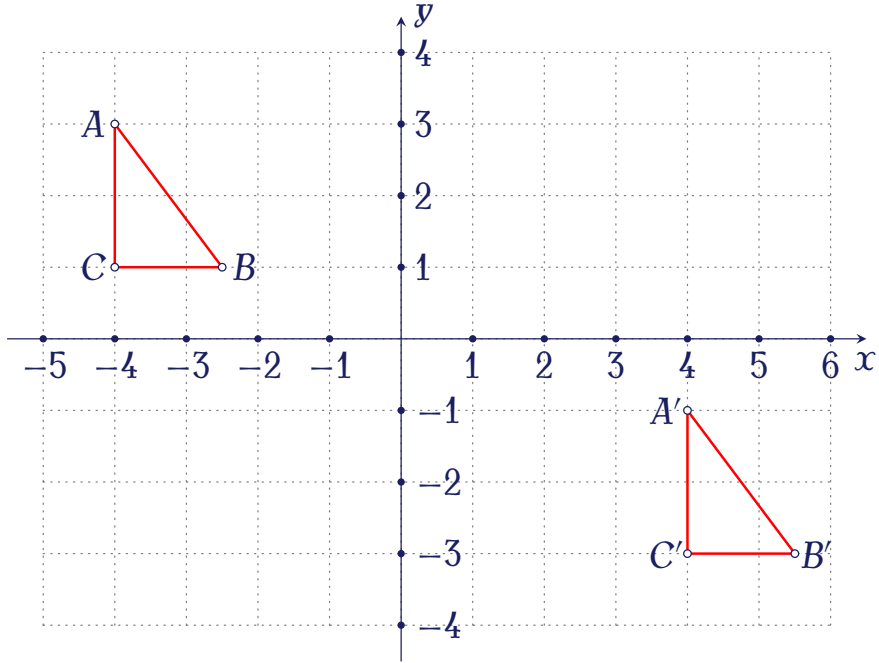
Tìm tọa độ vectơ $\overrightarrow{v}$ biết rằng phép tịnh tiến $\mathrm{T}_{\overrightarrow{v}}$ biến tam giác $ABC$ thành tam giác $A'B'C'$.
| $\overrightarrow{v}=(8;-4)$ | |
| $\overrightarrow{v}=(-8;4)$ | |
| $\overrightarrow{v}=(8;-3)$ | |
| $\overrightarrow{v}=(8;3)$ |
Biết rằng phép tịnh tiến theo vectơ $\overrightarrow{v}$ biến điểm $A(1;3)$ thành điểm $A'(1;7)$. Tìm tọa độ vectơ $\overrightarrow{v}$.
| $(0;-4)$ | |
| $(4;0)$ | |
| $(0;4)$ | |
| $(0;5)$ |
