Không gian mẫu của phép thử "Gieo một đồng xu cân đối và đồng chất \(2\) lần" có bao nhiêu biến cố (tập con)?

	\(4\)
	\(8\)
	\(12\)
	\(16\)

Gieo một đồng xu (cân đối và đồng chất) ba lần. Số phần tử của không gian mẫu là

	\(6\)
	\(3\)
	\(4\)
	\(8\)

Gieo ngẫu nhiên một đồng xu cân đối và đồng chất ba lần. Số phần tử của không gian mẫu là

	$6$
	$4$
	$8$
	$9$

Cho $3$ tấm bìa khác nhau trên đó đã được viết lên các chữ cái $K,Y,S$. Sau đó người ta thử trải ra ngẫu nhiên thành hàng ngang, hãy mô tả không gian mẫu của phép thử trên.

Một hộp có \(5\) viên bi xanh, \(6\) viên bi đỏ và \(7\) viên bi vàng. Chọn ngẫu nhiên \(5\) viên bi trong hộp. Tính xác suất để \(5\) viên bi được chọn có đủ \(3\) màu và số bi đỏ bằng với số bi vàng.

Một hộp chứa \(18\) quả cầu gồm \(8\) quả cầu màu xanh và \(10\) quả cầu màu trắng. Chọn ngẫu nhiên \(2\) quả cầu từ hộp đó. Tính xác suất để chọn được \(2\) quả cầu cùng màu.

Một bộ đề có \(10\) câu hỏi trắc nghiệm, trong đó có \(6\) câu Đại số và \(4\) câu Hình học. Bạn Nam bốc thăm chọn ngẫu nhiên \(3\) câu từ bộ đề. Hỏi xác suất để trong số ba câu bạn Nam chọn được có ít nhất một câu Hình học.

Có hai thùng đựng rượu Bầu Đá, một loại rượu nổi tiếng của thị xã An Nhơn, tỉnh Bình Định. Thùng thứ nhất đựng \(10\) chai gồm \(6\) chai rượu loại một và \(4\) chai rượu loại hai. Thùng thứ hai đựng \(8\) chai gồm \(5\) chai rượu loại một và \(3\) chai rượu loại hai. Lấy ngẫu nhiên mỗi thùng một chai, tính xác suất để lấy được ít nhất một chai rượu loại một. Biết rằng các chai rượu giống nhau về hình thức (rượu loại một và loại hai chỉ khác nhau về nồng độ cồn) và khả năng được chọn là như nhau.

Chọn ngẫu nhiên \(2\) học sinh từ một tổ có \(9\) học sinh. Biết rằng xác suất chọn được \(2\) học sinh nữ bằng \(\dfrac{5}{18}\), hỏi tổ đó có bao nhiêu học sinh nữ.

Lớp 11B có \(20\) học sinh gồm \(12\) nữ và \(8\) nam. Cần chọn ra \(2\) học sinh của lớp đi lao động. Tính xác suất để chọn ngẫu nhiên được \(2\) học sinh trong đó có cả nam và nữ.

Lấy ngẫu nhiên 1 thẻ từ một hộp chứa 20 thẻ, được đánh số từ 1 đến 20. Tìm xác suất để thẻ được lấy ra là số

1. Chẵn
2. Chia hết cho 3
3. Lẻ và chia hết cho 3

Một hộp đựng 4 viên bi xanh, 3 viên bi đỏ và 2 viên bi vàng. Chọn ngẫu nhiên 2 viên bi. Tính xác suất để chọn được 2 viên bi cùng màu.

Trền bàn có một cốc nước hình trụ chứa đầy nước, có chiều cao bằng 3 lần đường kính của đáy; một viên bi và một khối nón đều bằng thủy tinh. Biết viên bi là một khối cầu có đường kính bằng đường kính của cốc nước. Người ta từ từ thả vào cốc nước viên bi và khối nón sao cho đỉnh khối nón nằm trên mặt cầu (như hình vẽ) thì thấy nước trong cốc tràn ra ngoài.

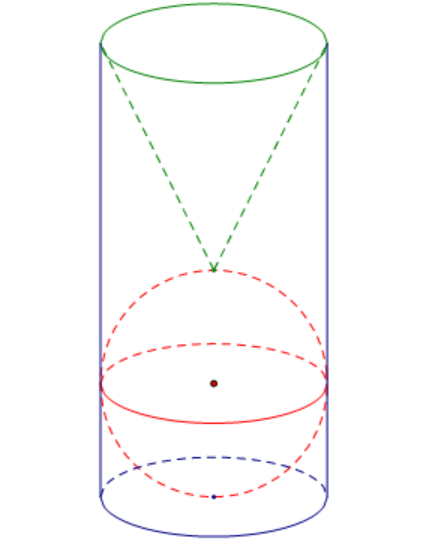
Tính tỉ số thể tích của lượng nước còn lại trong cốc và lượng nước ban đầu (bỏ qua bề dày của lớp vỏ thủy tinh).

Gieo ngẫu nhiên một con súc sắc cân đối và đồng chất $3$ lần. Khi đó số phần tử của không gian mẫu bằng

	$6\cdot6\cdot6$
	$6\cdot6\cdot5$
	$6\cdot5\cdot4$
	$6\cdot6$

Lớp 11A4 có \(16\) bạn nam và \(21\) bạn nữ. Rút thăm ngẫu nhiên để chọn hai bạn hát song ca. Không gian mẫu có bao nhiêu phần tử?

	\(336\)
	\(37\)
	\(1332\)
	\(666\)

Gieo đồng thời một đồng xu và một con súc sắc (cân đối và đồng chất), không gian mẫu có bao nhiêu phần tử?

	\(2\)
	\(6\)
	\(8\)
	\(12\)

Gieo một đồng xu cân đối và đồng chất \(2\) lần, không gian mẫu có bao nhiêu phần tử?

	\(2\)
	\(4\)
	\(6\)
	\(8\)

Gọi $A$ là biến cố của một phép thử. Phát biểu nào sau đây không đúng?

	\(nA>n\Omega\)
	\(A\subset\Omega\)
	\(0\leq P(A)\leq1\)
	\(P\left(\overline{A}\right)=1-P(A)\)

Gieo ngẫu nhiên một con súc sắc cân đối và đồng chất \(3\) lần. Khi đó \(n\left(\Omega\right)\) bằng

	\(216\)
	\(36\)
	\(18\)
	\(120\)

Gieo một đồng xu (cân đối và đồng chất) liên tiếp hai lần. Tìm không gian mẫu \(\Omega\).

	\(\Omega=\left\{S;N\right\}\)
	\(\Omega=\left\{SN;NN;SS\right\}\)
	\(\Omega=\left\{SN;NS;SS;NN\right\}\)
	\(\Omega=\left\{SN;NS\right\}\)