Số gia của hàm số $y=f(x)=x^2+2x-3$ ứng với số gia $\Delta x$ của đối số tại $x_0=1$ là
| $\Delta y=\Delta^2x-4\Delta x$ | |
| $\Delta y=\Delta^2x+2\Delta x$ | |
| $\Delta y=4\Delta x$ | |
| $\Delta y=\Delta^2x+4\Delta x$ |
Cho hàm số $y=f\left(x\right)$ xác định trên $\left(a;b\right)$, $x_0\in\left(a;b\right)$. Đạo hàm của hàm số $y=f\left(x\right)$ tại điểm $x_0$ là
| $f'\left(x_0\right)=\lim\limits_{\Delta y\to0}\dfrac{\Delta y}{\Delta x}$ | |
| $f'\left(x_0\right)=\lim\limits_{\Delta x\to0}\dfrac{\Delta y}{\Delta x}$ | |
| $f'\left(x_0\right)=\lim\limits_{x\to0}\dfrac{\Delta y}{\Delta x}$ | |
| $f'\left(x_0\right)=\lim\limits_{x\to0}\dfrac{\Delta x}{\Delta y}$ |
Tính tỷ số \(\dfrac{\Delta y}{\Delta x}\) của hàm số \(y=x^2-1\) theo \(x\) và \(\Delta x\).
| \(\dfrac{\Delta y}{\Delta x}=0\) | |
| \(\dfrac{\Delta y}{\Delta x}=\Delta x+2x\) | |
| \(\dfrac{\Delta y}{\Delta x}=2+\Delta x\) | |
| \(\dfrac{\Delta y}{\Delta x}=\Delta x\) |
Tính tỷ số \(\dfrac{\Delta y}{\Delta x}\) của hàm số \(y=3x+1\) theo \(x\) và \(\Delta x\).
| \(\dfrac{\Delta y}{\Delta x}=0\) | |
| \(\dfrac{\Delta y}{\Delta x}=1\) | |
| \(\dfrac{\Delta y}{\Delta x}=2\) | |
| \(\dfrac{\Delta y}{\Delta x}=3\) |
Tính số gia của hàm số \(y=\dfrac{1}{x}\) tại điểm \(x\neq0\) bất kì ứng với số gia \(\Delta x\).
| \(\Delta y=\dfrac{\Delta x}{x\left(x+\Delta x\right)}\) | |
| \(\Delta y=-\dfrac{\Delta x}{x\left(x+\Delta x\right)}\) | |
| \(\Delta y=-\dfrac{\Delta x}{x+\Delta x}\) | |
| \(\Delta y=\dfrac{\Delta x}{x+\Delta x}\) |
Tính số gia của hàm số \(y=\dfrac{x^2}{2}\) tại điểm \(x_0=-1\) ứng với số gia \(\Delta x\).
| \(\Delta y=\dfrac{1}{2}\left(\Delta x\right)^2-\Delta x\) | |
| \(\Delta y=\dfrac{1}{2}\left[\left(\Delta x\right)^2-\Delta x\right]\) | |
| \(\Delta y=\dfrac{1}{2}\left[\left(\Delta x\right)^2+\Delta x\right]\) | |
| \(\Delta y=\dfrac{1}{2}\left(\Delta x\right)^2+\Delta x\) |
Tính số gia của hàm số \(y=x^3+x^2+1\) tại điểm \(x_0\) ứng với số gia \(\Delta x=1\).
| \(\Delta y=3x_0^2+5x_0+3\) | |
| \(\Delta y=2x_0^3+3x_0^2+5x_0+2\) | |
| \(\Delta y=3x_0^2+5x_0+2\) | |
| \(\Delta y=3x_0^2-5x_0+2\) |
Tính số gia của hàm số \(y=x^2+2\) tại điểm \(x_0=2\) ứng với số gia \(\Delta x=1\).
| \(\Delta y=13\) | |
| \(\Delta y=9\) | |
| \(\Delta y=5\) | |
| \(\Delta y=2\) |
Cho hàm số $y=f(x)$ có đạo hàm trên $\mathbb{R}$ và có bảng xét dấu $f'(x)$ như sau:

Hỏi hàm số $y=f\big(x^2-2x\big)$ có bao nhiêu điểm cực tiểu?
| $1$ | |
| $3$ | |
| $2$ | |
| $4$ |
Cho hàm số $f(x)=\ln\big(x^2+1\big)$. Giá trị $f'(2)$ bằng
| $\dfrac{4}{5}$ | |
| $\dfrac{4}{3\ln2}$ | |
| $\dfrac{4}{2\ln5}$ | |
| $2$ |
Đạo hàm của hàm số $y=x^{2023}$ là
| $y'=2023x^{2023}$ | |
| $y'=2022x^{2023}$ | |
| $y'=2023x^{2022}$ | |
| $y'=\dfrac{1}{2023}x^{2022}$ |
Đạo hàm của hàm số $y=\dfrac{\ln2x}{x}$ là
| $y'=\dfrac{1-\ln2x}{x^2}$ | |
| $y'=\dfrac{\ln2x}{2x}$ | |
| $y'=\dfrac{\ln2x}{x^2}$ | |
| $y'=\dfrac{1}{2x}$ |
Đạo hàm của hàm số $y=\big(x^4+3\big)^{\tfrac{1}{3}}$ là
| $y'=\dfrac{4}{3}x^3\big(x^4+3\big)^{-\tfrac{2}{3}}$ | |
| $y'=\dfrac{1}{3}x^3\big(x^4+3\big)^{-\tfrac{2}{3}}$ | |
| $y'=\dfrac{4}{3}x^3\big(x^4+3\big)^{\tfrac{2}{3}}$ | |
| $y'=4x^3\big(x^4+3\big)^{-\tfrac{2}{3}}$ |
Cho hàm số $f(x)$ liên tục trên $\mathbb{R}$ và có bảng xét dấu của đạo hàm như sau:

Số điểm cực đại của hàm số đã cho là
| $3$ | |
| $1$ | |
| $2$ | |
| $0$ |
Cho hàm số $f(x)$ có bảng xét dấu của đạo hàm như sau:

Hàm số đã cho nghịch biến trên khoảng nào trong các khoảng dưới đây?
| $(-\infty;2)$ | |
| $(-\infty;-1)$ | |
| $(-1;2)$ | |
| $(-1;+\infty)$ |
Cho hàm số $y=f(x)$ có $f'(x)$ liên tục trên $\mathbb{R}$ và đồ thị $f'(x)$ như hình bên.
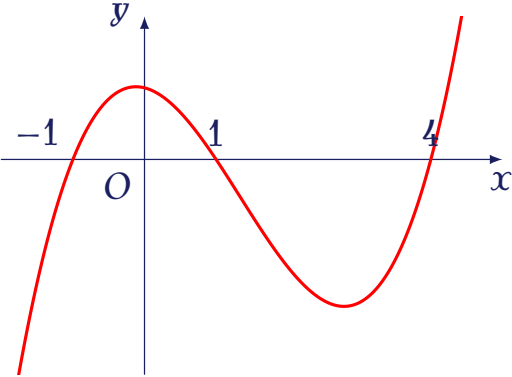
Hàm số đã cho nghịch biến trên khoảng nào sau đây?
| $(-\infty;0)$ | |
| $(-1;1)$ | |
| $(1;4)$ | |
| $(1;+\infty)$ |
Đạo hàm của hàm số $y=(x+1)^\pi$ là
| $y'=\pi(x+1)^\pi$ | |
| $y'=(\pi-1)(x+1)^{\pi-1}$ | |
| $y'=\pi(x+1)^{\pi-1}$ | |
| $y'=(x+1)^{\pi-1}$ |
Đạo hàm của hàm số $y=\ln\big(x^2+2\big)$ là
| $y'=\dfrac{1}{x^2+2}$ | |
| $y'=\dfrac{x}{x^2+2}$ | |
| $y'=\dfrac{2}{x^2+2}$ | |
| $y'=\dfrac{2x}{x^2+2}$ |
Cho hàm số $y=f(x)$ có bảng xét dấu đạo hàm như sau:

Số điểm cực trị của hàm số đã cho bằng
| $3$ | |
| $0$ | |
| $1$ | |
| $2$ |
Giá trị nhỏ nhất của hàm số $y=x^3+3x^2-1$ trên đoạn $[-1;1]$ bằng
| $3$ | |
| $-1$ | |
| $1$ | |
| $2$ |
