Đạo hàm của hàm số \(y=\dfrac{-x^2+3x-3}{2(x-1)}\) là biểu thức có dạng \(\dfrac{ax^2+bx}{2(x-1)^2}\). Khi đó, tích \(a\cdot b\) bằng
| \(-1\) | |
| \(6\) | |
| \(4\) | |
| \(-2\) |
Cho \(\displaystyle\int\limits_{0}^{1}\dfrac{x^2+1}{x+1}\mathrm{\,d}x=a+b\ln c\), với \(a\in\mathbb{Q}\), \(b\in\mathbb{Z}\), \(c\) là số nguyên tố. Ta có \(2a+b+c\) bằng
| \(5\) | |
| \(4\) | |
| \(3\) | |
| \(2\) |
Giả sử \(\displaystyle\int\limits_{3}^{5}\dfrac{\mathrm{d}x}{x^2-x}=a\ln5+b\ln3+c\ln2\). Tính giá trị biểu thức \(S=-2a+b+3c^2\).
| \(S=3\) | |
| \(S=6\) | |
| \(S=-2\) | |
| \(S=0\) |
Biết \(I=\displaystyle\int\limits_1^2\dfrac{dx}{\left(2x+2\right)\sqrt{x}+2x\sqrt{x+1}}=\dfrac{\sqrt{a}-\sqrt{b}-c}{2}\) với \(a\), \(b\), \(c\) là các số nguyên dương. Tính \(P=a-b+c\).
| \(P=24\) | |
| \(P=12\) | |
| \(P=18\) | |
| \(P=22\) |
Biết \(\displaystyle\int\limits_1^3\dfrac{\mathrm{\,d}x}{\sqrt{x+1}-\sqrt{x}}=a\sqrt{3}+b\sqrt{2}+c\) với \(a\), \(b\), \(c\) là các số hữu tỷ. Tính \(P =a+b+c\).
| \(P=\dfrac{13}{2}\) | |
| \(P=\dfrac{16}{3}\) | |
| \(P=5\) | |
| \(P=\dfrac{2}{3}\) |
Biết \(\displaystyle\int\limits_0^1\dfrac{x}{\sqrt{x+1}}\mathrm{\,d}x=\dfrac{a}{b}\left(c-\sqrt{2}\right)\) với \(\dfrac{a}{b}\) là phân số tối giản. Tính \(a+b+c\).
| \(-1\) | |
| \(7\) | |
| \(3\) | |
| \(1\) |
Cho hàm số $f(x)=\dfrac{ax-1}{bx+c}\,(a,\,b,\,c\in\mathbb{R})$ có bảng biến thiên như hình bên.
Giá trị của $a-b-c$ thuộc khoảnh nào sau đây?
| $\left(-1;0\right)$ | |
| $\left(-2;-1\right)$ | |
| $\left(1;2\right)$ | |
| $\left(0;1\right)$ |
Biết $\left(x^5-3x^4+2019\right)^{\prime}=ax^4+bx^3$. Tìm $S=a+b$.
| $S=-7$ | |
| $S=7$ | |
| $S=17$ | |
| $S=12$ |
Cho $\displaystyle\displaystyle\int\limits_{\tfrac{\pi}{6}}^{\tfrac{\pi}{4}}\cos4x\cos x\mathrm{\,d}x=\dfrac{\sqrt{2}}{a}+\dfrac{b}{c}$ với $a,\,b,\,c$ là các số nguyên, $c< 0$ và $\dfrac{b}{c}$ tối giản. Tổng $a+b+c$ bằng
| $-77$ | |
| $-17$ | |
| $103$ | |
| $43$ |
Cho hàm số $y=f\left(x\right)$ liên tục trên $\mathbb{R}\setminus\left\{0;-1\right\}$ thỏa mãn điều kiện $f\left(1\right)=-2\ln2$ và $x\left(x+1\right)\cdot f'\left(x\right)+f\left(x\right)=x^2+x$. Giá trị $f\left(2\right)=a+b\ln3$, với $a,\,b\in\mathbb{Q}$. Tính $a^2+b^2$.
Biết rằng $\displaystyle\displaystyle\int\limits_{1}^{5}\dfrac{3}{x^2+3x}\mathrm{d}x=a\ln5+b\ln2$ $\left(a,\,b\in\mathbb{Z}\right)$. Mệnh đề nào sau đây đúng?
| $a+2b=0$ | |
| $2a-b=0$ | |
| $a-b=0$ | |
| $a+b=0$ |
Cho hàm số $f\left(x\right)=x^3+ax^2+bx+c$ với $a,\,b,\,c\in\mathbb{R}$. Hãy xác định các số $a,\,b,\,c$ biết rằng $f'\left(\dfrac{1}{3}\right)=0$ và đồ thị của hàm số $y=f\left(x\right)$ đi qua các điểm $\left(-1;-3\right)$ và $\left(1;-1\right)$.
Cho $\displaystyle\displaystyle\int\limits_0^1\dfrac{\mathrm{d}x}{\sqrt{x+1}+\sqrt{x}}=\dfrac{2}{3}\left(\sqrt{a}-b\right)$ với $a$, $b$ là các số dương. Giá trị của biểu thức $T=a+b$ là
| $10$ | |
| $7$ | |
| $6$ | |
| $8$ |
Biết $\displaystyle\displaystyle\int\limits_{-1}^1\left(\dfrac{9}{x-3}-\dfrac{7}{x-2}\right)\mathrm{\,d}x=a\ln{3}-b\ln{2}$. Tính giá trị $P=a^2+b^2$.
| $P=32$ | |
| $P=130$ | |
| $P=2$ | |
| $P=16$ |
Biết $\displaystyle\displaystyle\int\limits_0^1x\sqrt{x^2+4}\mathrm{\,d}x=\dfrac{1}{a}\left(\sqrt{b^3}-c\right)$. Tính $Q=abc$.
| $Q=120$ | |
| $Q=15$ | |
| $Q=-120$ | |
| $Q=40$ |
Cho hàm số $y=\begin{cases}x^2+ax+b&\text{khi }x\ge2\\ x^3-x^2-8x+10&\text{khi }x<2\end{cases}$. Biết hàm số có đạo hàm tại điểm $x=2$. Giá trị của $a^2+b^2$ bằng
| $20$ | |
| $17$ | |
| $18$ | |
| $25$ |
Cho hàm số $f\left(x\right)=\begin{cases}ax^2+bx+1&\text{khi }x\ge0\\ ax-b-1&\text{khi }x<0\end{cases}$. Khi hàm số $f\left(x\right)$ có đạo hàm tại $x_0=0$, hãy tính $T=a+2b$.
| $T=-4$ | |
| $T=0$ | |
| $T=-6$ | |
| $T=4$ |
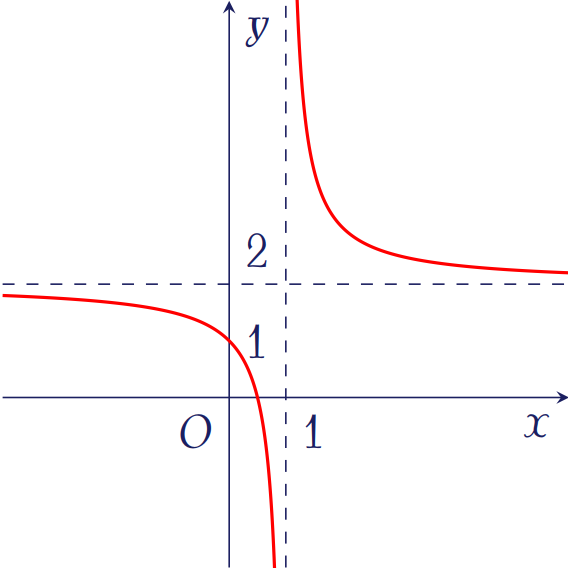
Cho hàm số \(y=\dfrac{ax-1}{bx+c}\) có đồ thị như hình trên. Tính giá trị biểu thức \(T=a+2b+3c\).
| \(T=1\) | |
| \(T=2\) | |
| \(T=3\) | |
| \(T=4\) |
Biết \(\displaystyle\int\limits_{1}^{2}\dfrac{\mathrm{d}x}{(x+1)(2x+1)}=a\ln2+b\ln3+c\ln5\). Khi đó giá trị \(a+b+c\) bằng
| \(1\) | |
| \(0\) | |
| \(2\) | |
| \(-3\) |
Tìm \(m\) để bất phương trình \(x+\dfrac{4}{x-1}\geq m\) có nghiệm trên khoảng \((-\infty;1)\).
| \(m\leq3\) | |
| \(m\leq-3\) | |
| \(m\leq5\) | |
| \(m\leq-1\) |
