Rút gọn biểu thức \(P=\dfrac{a^{\sqrt{3}+1}\cdot a^{2-\sqrt{3}}}{\left(a^{\sqrt{2}-2}\right)^{\sqrt{2}+2}}\) với \(a>0\).
| \(P=a\) | |
| \(P=a^3\) | |
| \(P=a^4\) | |
| \(P=a^5\) |
Kết quả viết dưới dạng lũy thừa với số mũ hữu tỉ của biểu thức \(F=\dfrac{\sqrt{a\sqrt{a\sqrt{a\sqrt{a}}}}}{a^{\tfrac{11}{16}}}\) với \(a>0\) là
| \(F=a^{\tfrac{1}{4}}\) | |
| \(F=a^{\tfrac{3}{8}}\) | |
| \(F=a^{\tfrac{1}{2}}\) | |
| \(F=a^{\tfrac{3}{4}}\) |
Tập xác định của hàm số $y=x^{\sqrt{2}-1}$ là
| $\big(-\infty;\sqrt{2}\big)$ | |
| $\mathbb{R}\setminus\{0\}$ | |
| $\mathbb{R}$ | |
| $(0;+\infty)$ |
Rút gọn biểu thức $Q=b^{\tfrac{5}{3}}:\sqrt[3]{b^2}$, $b>0$.
| $Q=b$ | |
| $Q=b^{\tfrac{1}{3}}$ | |
| $Q=b^2$ | |
| $Q=\sqrt{b^4}$ |
Đạo hàm của hàm số $y=x^{2023}$ là
| $y'=2023x^{2023}$ | |
| $y'=2022x^{2023}$ | |
| $y'=2023x^{2022}$ | |
| $y'=\dfrac{1}{2023}x^{2022}$ |
Với $m,\,n$ là hai số thực bất kỳ, $a$ là số thực dương tùy ý. Khẳng định nào sau đây sai?
| $a^{m\cdot n}=\big(a^n\big)^m$ | |
| $a^{m-n}=\dfrac{a^m}{a^n}$ | |
| $a^{m+n}=a^m+a^n$ | |
| $a^{m\cdot n}=\big(a^m\big)^n$ |
Đạo hàm của hàm số $y=\big(x^4+3\big)^{\tfrac{1}{3}}$ là
| $y'=\dfrac{4}{3}x^3\big(x^4+3\big)^{-\tfrac{2}{3}}$ | |
| $y'=\dfrac{1}{3}x^3\big(x^4+3\big)^{-\tfrac{2}{3}}$ | |
| $y'=\dfrac{4}{3}x^3\big(x^4+3\big)^{\tfrac{2}{3}}$ | |
| $y'=4x^3\big(x^4+3\big)^{-\tfrac{2}{3}}$ |
Biểu thức $a^{\tfrac{4}{3}}\sqrt{a}$ ($a>0$) viết dưới dạng lũy thừa với số mũ hữu tỉ là
| $a^{\tfrac{11}{6}}$ | |
| $a^{\tfrac{10}{3}}$ | |
| $a^{\tfrac{7}{3}}$ | |
| $a^{\tfrac{5}{6}}$ |
Số $\dfrac{\sqrt[3]{16}}{8}$ viết dưới dạng lũy thừa với số mũ hữu tỉ là
| $2^{\tfrac{13}{3}}$ | |
| $2^{-\tfrac{13}{3}}$ | |
| $2^{\tfrac{5}{3}}$ | |
| $2^{-\tfrac{5}{3}}$ |
Đạo hàm của hàm số $y=(x+1)^\pi$ là
| $y'=\pi(x+1)^\pi$ | |
| $y'=(\pi-1)(x+1)^{\pi-1}$ | |
| $y'=\pi(x+1)^{\pi-1}$ | |
| $y'=(x+1)^{\pi-1}$ |
Cho hàm số $y=\big(2x^2-1\big)^{\tfrac{1}{2}}$. Giá trị của hàm số đã cho tại điểm $x=2$ bằng
| $3$ | |
| $\sqrt{7}$ | |
| $\sqrt{3}$ | |
| $7$ |
Trên khoảng $(0;+\infty)$, đạo hàm của hàm số $y=x^{\pi}$ là
| $y'=\pi x^{\pi-1}$ | |
| $y'=x^{\pi-1}$ | |
| $y'=\dfrac{1}{\pi}x^{\pi-1}$ | |
| $y'=\pi x^{\pi}$ |
Tập xác định của hàm số $y=(x+2)^{-2022}$ là
| $[-2;+\infty)$ | |
| $(-2;+\infty)$ | |
| $\mathbb{R}\setminus\{-2\}$ | |
| $\mathbb{R}$ |
Cho $x,\,y$ là hai số thực dương và $m,\,n$ là hai số thực tùy ý. Đẳng thức nào sau đây là sai?
| $\dfrac{x^m}{x^n}=x^{m-n}$ | |
| $(xy)^n=x^n\cdot y^n$ | |
| $\dfrac{x^m}{y^n}=\left(\dfrac{x}{y}\right)^{m-n}$ | |
| $\big(x^n\big)^m=x^{n\cdot m}$ |
Cho hàm số $f(x)=\big(1-\sqrt[4]{x}\big)\big(1+\sqrt[4]{x}\big)\big(1+\sqrt{x}\big)(1+x)$. Tính $f\left(\dfrac{1}{2^{64}}\right)$.
| $1-\dfrac{1}{2^{128}}$ | |
| $1+\dfrac{1}{2^{64}}$ | |
| $1+\dfrac{1}{2^{128}}$ | |
| $1-\dfrac{1}{2^{64}}$ |
Rút gọn biểu thức $A=\dfrac{\sqrt[3]{a^7}\cdot a^{\tfrac{11}{3}}}{a^4\cdot\sqrt[7]{a^{-5}}}$ với $a>0$ ta được kết quả là
| $A=a^{\tfrac{9}{7}}$ | |
| $A=a^{\tfrac{19}{7}}$ | |
| $A=a^{\tfrac{43}{5}}$ | |
| $A=a^{\tfrac{157}{105}}$ |
Cho đồ thị các hàm số $y=x^\alpha$ và $y=x^\beta$ trên khoảng $(0;+\infty)$.
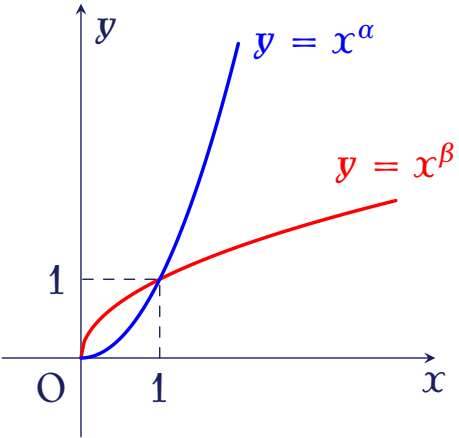
Mệnh đề nào dưới đây đúng?
| $0< \alpha< 1< \beta$ | |
| $\alpha< 0< 1< \beta$ | |
| $0< \beta< 1< \alpha$ | |
| $\beta< 0< 1< \alpha$ |
Đạo hàm của hàm số $y=\big(x^4+3\big)^{\tfrac{1}{3}}$ là
| $y'=\dfrac{4}{3}x^3\big(x^4+3\big)^{-\tfrac{2}{3}}$ | |
| $y'=\dfrac{1}{3}x^3\big(x^4+3\big)^{-\tfrac{2}{3}}$ | |
| $y'=\dfrac{4}{3}x^3\big(x^4+3\big)^{\tfrac{2}{3}}$ | |
| $y'=4x^3\big(x^4+3\big)^{-\tfrac{2}{3}}$ |
Đạo hàm của hàm số $y=x^{-3}$ là
| $y'=-x^{-4}$ | |
| $y'=-\dfrac{1}{2}x^{-2}$ | |
| $y'=-\dfrac{1}{3}x^{-4}$ | |
| $y'=-3x^{-4}$ |
Cho các số thực $a,\,b$ thỏa $\left(\sqrt{2019}-\sqrt{2018}\right)^a>\left(\sqrt{2019}-\sqrt{2018}\right)^b$. Kết luận nào sau đây đúng?
| $a>b$ | |
| $a< b$ | |
| $a=b$ | |
| $a\geq b$ |
