Tính diện tích \(S\) của hình phẳng \((H)\) giới hạn bởi đồ thị hàm số \(y=-x^3+3x^2-2\), hai trục tọa độ và đường thẳng \(x=2\).
| \(S=\dfrac{1}{3}\) | |
| \(S=\dfrac{19}{2}\) | |
| \(S=\dfrac{9}{2}\) | |
| \(S=\dfrac{5}{2}\) |
Tính diện tích \(S\) của hình phẳng giới hạn bởi đồ thị hàm số \(y=3^x\), trục \(Ox\) và hai đường thẳng \(x=-1\), \(x=2\).
| \(S=\dfrac{26}{3}\) | |
| \(S=12\) | |
| \(S=\dfrac{12}{\ln3}\) | |
| \(S=\dfrac{26}{3\ln3}\) |
Cho hàm số $y=2^x$ có đồ thị là đường cong trong hình bên.
Diện tích $S$ của hình phẳng được tô đậm trong hình bằng
| $S=\displaystyle\displaystyle\int\limits_{1}^{2}2^x\mathrm{\,d}x$ | |
| $S=\displaystyle\displaystyle\int\limits_{0}^{2}2^{2x}\mathrm{\,d}x$ | |
| $S=\pi\displaystyle\displaystyle\int\limits_{0}^{2}2^x\mathrm{\,d}x$ | |
| $S=\displaystyle\displaystyle\int\limits_{0}^{2}2^x\mathrm{\,d}x$ |
Tính diện tích $S$ của hình phẳng giới hạn bởi đồ thị hàm số $y=\cos{x}+2$, trục hoành và các đường thẳng $x=0$, $x=\dfrac{\pi}{4}$.
| $S=\dfrac{\pi}{2}-\dfrac{\sqrt{2}}{2}$ | |
| $S=\dfrac{\pi}{4}+\dfrac{7}{10}$ | |
| $S=\dfrac{\pi}{2}+\dfrac{\sqrt{2}}{2}$ | |
| $S=\dfrac{\pi}{4}+\dfrac{\sqrt{2}}{2}$ |
Cho hàm số $y=x^4-4x^2+m$. Tìm $m$ để đồ thị của hàm số cắt trục hoành tại $4$ điểm phân biệt sao cho hình phẳng giới hạn bởi đồ thị với trục hoành có diện tích phần phía trên trục hoành bằng diện tích phần phía dưới trục hoành. Khi đó $m=\dfrac{a}{b}$ với $\dfrac{a}{b}$ là phân số tối giản. Tính $a+2b$.
| $37$ | |
| $38$ | |
| $0$ | |
| $29$ |
Cho hàm số $f(x)=x^4-5x^2+4$. Gọi $S$ là diện tích hình phẳng giới hạn bởi đồ thị hàm số $y=f(x)$ và trục hoành. Mệnh đề nào sau đây là sai?
| $S=2\displaystyle\displaystyle\int\limits_{0}^{2}\left|f(x)\right|\mathrm{\,d}x$ | |
| $S=2\left|\displaystyle\displaystyle\int\limits_{0}^{2}f(x)\mathrm{\,d}x\right|$ | |
| $S=2\left|\displaystyle\displaystyle\int\limits_{0}^{1}f(x)\mathrm{\,d}x\right|+2\left|\displaystyle\displaystyle\int\limits_{1}^{2}f(x)\mathrm{\,d}x\right|$ | |
| $S=\displaystyle\displaystyle\int\limits_{-2}^{2}\left|f(x)\right|\mathrm{\,d}x$ |
Tiếp tuyến của đường cong \(\left(\mathscr{C}\right)\colon y=\dfrac{2x+1}{x-1}\) tại điểm \(M(2;5)\) cắt các trục tọa độ \(Ox\), \(Oy\) lần lượt tại \(A\) và \(B\). Tính diện tích tam giác \(OAB\).
| \(\dfrac{121}{6}\) | |
| \(\dfrac{121}{3}\) | |
| \(-\dfrac{121}{6}\) | |
| \(-\dfrac{121}{3}\) |
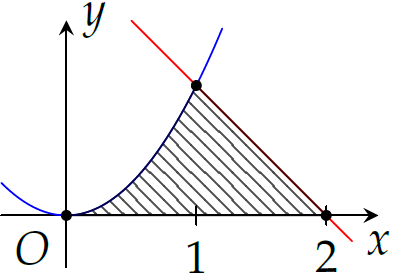
Tính diện tích hình phẳng tạo thành bởi parabol \(y=x^2\), đường thẳng \(y=-x+2\) và trục hoành trên đoạn \([0;2]\) (phần gạch sọc trong hình vẽ).
| \(\dfrac{5}{6}\) | |
| \(\dfrac{7}{6}\) | |
| \(\dfrac{2}{3}\) | |
| \(\dfrac{3}{5}\) |
Nếu hàm số \(y=f(x)\) liên tục trên đoạn \([a;b]\) thì diện tích \(S\) của hình phẳng giới hạn bởi đồ thị hàm số \(y=f(x)\), trục hoành và hai đường thẳng \(x=a\), \(x=b\) là
| \(\displaystyle\int\limits_{a}^{b}\left|f(x)-g(x)\right|\mathrm{\,d}x\) | |
| \(\displaystyle\int\limits_{b}^{a}\left|f(x)\right|\mathrm{\,d}x\) | |
| \(\displaystyle\int\limits_{a}^{b}f(x)\mathrm{\,d}x\) | |
| \(\displaystyle\int\limits_{a}^{b}\left|f(x)\right|\mathrm{\,d}x\) |
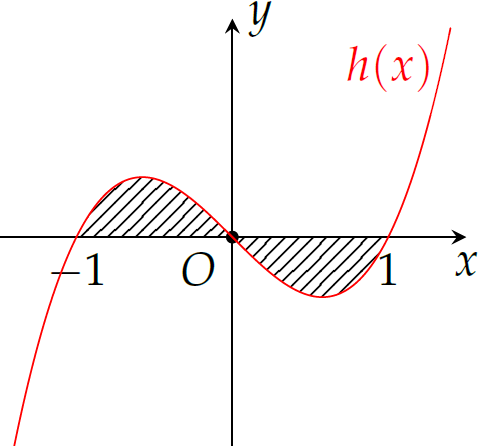
Cho đồ thị hàm số \(y=h(x)\). Diện tích hình phẳng (phần gạch chéo trong hình vẽ) bằng
| \(\displaystyle\int\limits_{-1}^{0}h(x)\mathrm{\,d}x+\displaystyle\int\limits_{0}^{1}h(x)\mathrm{\,d}x\) | |
| \(\displaystyle\int\limits_{-1}^{1}h(x)\mathrm{\,d}x\) | |
| \(\displaystyle\int\limits_{-1}^{0}h(x)\mathrm{\,d}x+\displaystyle\int\limits_{1}^{0}h(x)\mathrm{\,d}x\) | |
| \(-\displaystyle\int\limits_{-1}^{0}h(x)\mathrm{\,d}x+\displaystyle\int\limits_{0}^{1}h(x)\mathrm{\,d}x\) |
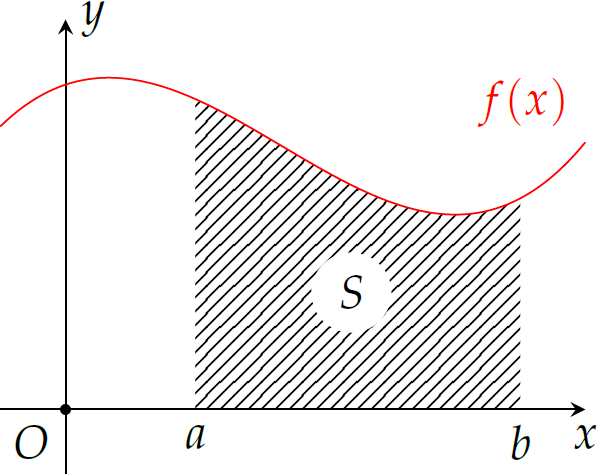
Diện tích hình phẳng \(S\) đối với hình vẽ trên là
| \(S=-\displaystyle\int\limits_{a}^{b}f(x)\mathrm{\,d}x\) | |
| \(S=\displaystyle\int\limits_{a}^{b}f(x)\mathrm{\,d}x\) | |
| \(S=\displaystyle\int\limits_{b}^{a}f(x)\mathrm{\,d}x\) | |
| \(S=\displaystyle\int\limits_{a}^{b}-f(x)\mathrm{\,d}x\) |
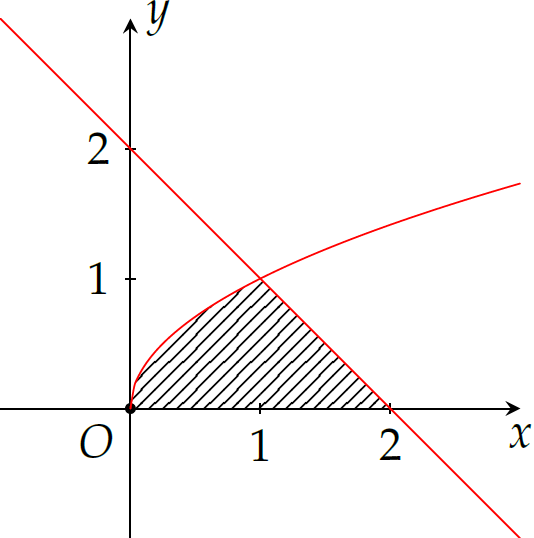
Cho \((H)\) là hình phẳng giới hạn bởi đồ thị của các hàm số \(y=\sqrt{x}\), \(y=0\), \(y=2-x\). Diện tích của \((H)\) là
| \(\dfrac{4\sqrt{2}-1}{3}\) | |
| \(\dfrac{8\sqrt{2}+3}{6}\) | |
| \(\dfrac{7}{6}\) | |
| \(\dfrac{5}{6}\) |
Tính diện tích hình phẳng giới hạn bởi \(\left(\mathscr{C}\right)\colon y=x^4-2x^2+1\) và trục hoành.
| \(\dfrac{8}{15}\) | |
| \(-\dfrac{15}{16}\) | |
| \(\dfrac{15}{8}\) | |
| \(\dfrac{16}{15}\) |
Tính diện tích hình phẳng giới hạn bởi các đường \(y=-x^2+4x-3\), \(x=0\), \(x=3\), \(Ox\).
| \(-\dfrac{8}{3}\) | |
| \(-\dfrac{4}{3}\) | |
| \(\dfrac{4}{3}\) | |
| \(\dfrac{8}{3}\) |
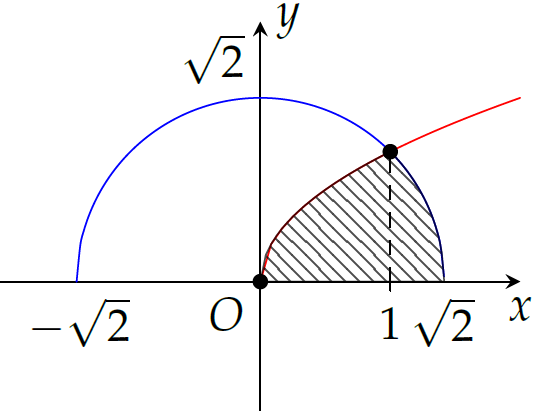
Cho \((H)\) là hình phẳng giới hạn bởi đường cong có phương trình \(y=\sqrt{x}\), nửa đường tròn có phương trình \(y=\sqrt{2-x^2}\) (với \(0\leq x\leq\sqrt{2}\)) và trục hoành (phần tô đậm trong hình vẽ). Diện tích của \((H)\) bằng
| \(\dfrac{3\pi+2}{12}\) | |
| \(\dfrac{4\pi+2}{12}\) | |
| \(\dfrac{3\pi+1}{12}\) | |
| \(\dfrac{4\pi+1}{6}\) |
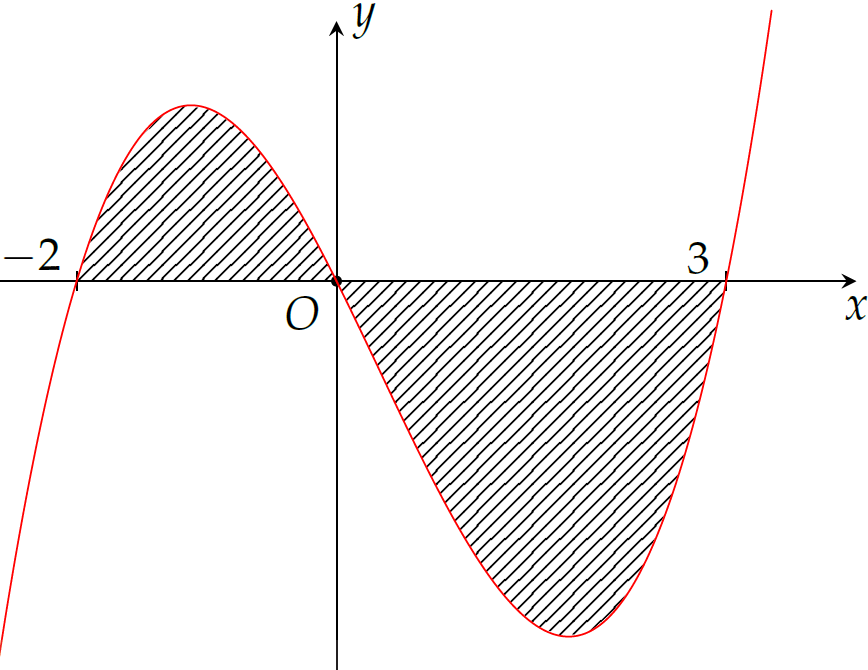
Cho đồ thị hàm số \(y=f(x)\) như hình vẽ và \(\displaystyle\int\limits_{-2}^{0}f(x)\mathrm{\,d}x=a\), \(\displaystyle\int\limits_{0}^{3}f(x)\mathrm{\,d}x=b\). Tính diện tích của phần được gạch chéo theo \(a\) và \(b\).
| \(\dfrac{a+b}{2}\) | |
| \(a-b\) | |
| \(b-a\) | |
| \(a+b\) |
Cho hàm số \(f(x)\) liên tục trên đoạn \([a;b]\). Diện tích hình phẳng giới hạn bởi đường cong \(y=f(x)\), trục hoành, các đường thẳng \(x=a\), \(x=b\) là
| \(\displaystyle\int\limits_{b}^{a}f(x)\mathrm{\,d}x\) | |
| \(\displaystyle\int\limits_{a}^{b}f(x)\mathrm{\,d}x\) | |
| \(\displaystyle\int\limits_{a}^{b}\left|f(x)\right|\mathrm{\,d}x\) | |
| \(-\displaystyle\int\limits_{a}^{b}f(x)\mathrm{\,d}x\) |
Cho hình phẳng \(D\) giới hạn bởi đường cong \(y=\mathrm{e}^x\), trục hoành và các đường thẳng \(x=0\), \(x=1\). Khối tròn xoay tạo thành khi quay \(D\) quanh trục hoành có thể tích \(V\) bằng
| \(V=\dfrac{\mathrm{e}^2-1}{2}\) | |
| \(V=\dfrac{\pi\left(\mathrm{e}^2+1\right)}{2}\) | |
| \(V=\dfrac{\pi\left(\mathrm{e}^2-1\right)}{2}\) | |
| \(V=\dfrac{\pi\mathrm{e}^2}{2}\) |
Gọi \((H)\) là hình phẳng giới hạn bởi các đường \(y=4^x\), \(y=0\), \(x=1\) và \(x=3\). Thể tích \(V\) của khối tròn xoay tạo thành khi quay \((H)\) quanh trục \(Ox\) được xác định bởi công thức
| \(V=\pi\displaystyle\int\limits_{1}^{3}4^{2x}\mathrm{\,d}x\) | |
| \(V=\displaystyle\int\limits_{1}^{3}4^{x+1}\mathrm{\,d}x\) | |
| \(V=\pi\displaystyle\int\limits_{1}^{3}4^{2x+1}\mathrm{\,d}x\) | |
| \(V=\displaystyle\int\limits_{1}^{3}16^x\mathrm{\,d}x\) |
Gọi \((H)\) là hình phẳng giới hạn bởi các đường \(y=3^x\), \(y=0\), \(x=0\) và \(x=3\). Thể tích \(V\) của khối tròn xoay tạo thành khi quay \((H)\) quanh trục \(Ox\) được xác định bởi công thức
| \(V=\pi\displaystyle\int\limits_{0}^{3}3^{x+1}\mathrm{\,d}x\) | |
| \(V=\displaystyle\int\limits_{0}^{3}3^{x+1}\mathrm{\,d}x\) | |
| \(V=\pi\displaystyle\int\limits_{0}^{3}9^x\mathrm{\,d}x\) | |
| \(V=\displaystyle\int\limits_{0}^{3}9^x\mathrm{\,d}x\) |
